QA-L10 QA-LSD Line
QA-L10 is the line with the Least Sum of Squared Distances of the QA-vertices to this line.
It is the counterpart of QL-P26 in a Quadrilateral which is the point with Least Sum of Squared Distances from this point to the QL-Lines.
It is described by J.L. Coolidge in [25]. He proves that the QA-Centroid will lie on this line. Unfortunately his proposed construction doesn’t produce the desired result.
Next construction uses properties of the Complex Plane. See [34], QFG-messages #1585, #1590.
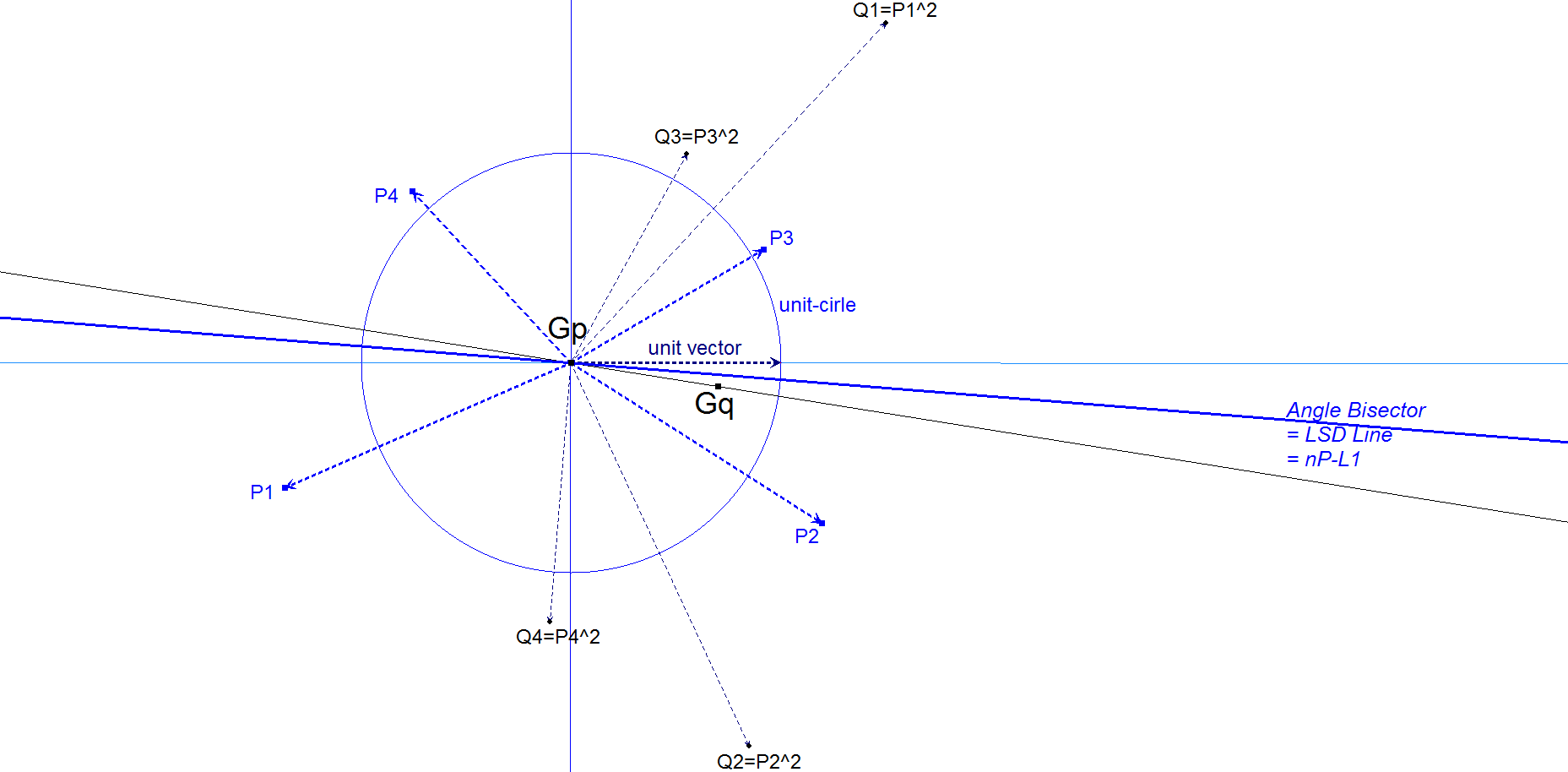
Draw a random couple of perpendicular lines intersecting in QA-P1 as x-axis and y-axis.
Let the 4 vertices of the QA be represented by complex numbers zi = xi + i yi.
The Centroid of the QA-vertices is the point QA-P1 where z = 0.
Let the QA-Pz = Centroid of the points represented by zi2 .
The searched LSD line is the angle bisector of the x-axis and the line QA-P1.QA-Pz.
The same type of construction can be used for any number of points.
Another construction can be found at [34], QFG-message #1611.
CT-Coefficients:
(Ua + (r-q) W : Ub + (p-r) W : Uc + (q-p) W)
where:
Ua= a2 (r-q) (p2+5 p q+4 q2+5 p r+5 q r+4 r2)
+ b2 (-2 p3-4 p2 q+p q2+3 q3-4 p2 r+2 p q r+6 q2 r-5 p r2+3 q r2)
+ c2 (2 p3+4 p2 q+5 p q2+4 p2 r-2 p q r-3 q2 r-p r2-6 q r2-3 r3)
Ub= a2 (-3 p3-p2 q+4 p q2+2 q3-6 p2 r-2 p q r+4 q2 r-3 p r2+5 q r2)
+ b2 (p-r) (4 p2+5 p q+q2+5 p r+5 q r+4 r2)
+ c2 (-5 p2 q-4 p q2-2 q3+3 p2 r+2 p q r-4 q2 r+6 p r2+q r2+3 r3)
Uc= a2 (3 p3+6 p2 q+3 p q2+p2 r+2 p q r-5 q2 r-4 p r2-4 q r2-2 r3)
+ b2 (-3 p2 q-6 p q2-3 q3+5 p2 r-2 p q r-q2 r+4 p r2+4 q r2+2 r3)
+ c2 (q-p) (4 p2+5 p q+4 q2+5 p r+5 q r+r2)
W = Sqrt[
( a4 (3 p2+4 p q+4 q2+6 p r+4 q r+3 r2) (3 p2+6 p q+3 q2+4 p r+4 q r+4 r2)
+ b4 (4 p2+4 p q+3 q2+4 p r+6 q r+3 r2) (3 p2+6 p q+3 q2+4 p r+4 q r+4 r2)
+ c4 (3 p2+4 p q+4 q2+6 p r+4 q r+3 r2) (4 p2+4 p q+3 q2+4 p r+6 q r+3 r2)
– 2 b2 c2 (p2+3 p q+2 q2+3 p r+q r+2 r2) (4 p2+4 p q+3 q2+4 p r+6 q r+3 r2)
– 2 a2 c2 (2 p2+3 p q+q2+p r+3 q r+2 r2) (3 p2+4 p q+4 q2+6 p r+4 q r+3 r2)
– 2 a2 b2 (2 p2+p q+2 q2+3 p r+3 q r+r2) (3 p2+6 p q+3 q2+4 p r+4 q r+4 r2))]
The algebraic least distance is: (A0 (T1 + V1 W)) / (2 (T2 + V2 W))
The algebraic largest distance for the perpendicular line through QA-P1 is: (A0 (T1 – V1 W)) / (2 (T2 – V2 W))
where:
A0 = (a-b-c) (a+b-c) (a-b+c) (a+b+c)
V1 = (p2-p q+q2-p r-q r+r2)
V2 = +a2 (p+q-2 r) (p-2q+r) + b2 (p+q-2 r) (-2 p+q+r) + c2 (-2 p+q+r) (p-2q+r)
T1 = c2 ( 2 p4 – 5 p3 q – 5 p2 q2 – 5 p q3 + 2 q4 + 5 p3 r + p2 q r + p q2 r + 5 q3 r + 4 p2 r2 – 2 p q r2 + 4 q2 r2 – 2 p r3 – 2 q r3 – 3 r4) +
a2 (-3 p4 – 2 p3 q + 4 p2 q2 + 5 p q3 + 2 q4 – 2 p3 r – 2 p2 q r + p q2 r – 5 q3 r + 4 p2 r2 + p q r2 – 5 q2 r2 + 5 p r3 – 5 q r3 + 2 r4) +
b2 ( 2 p4 + 5 p3 q + 4 p2 q2 – 2 p q3 – 3 q4 – 5 p3 r + p2 q r – 2 p q2 r – 2 q3 r – 5 p2 r2 + p q r2 + 4 q2 r2 – 5 p r3 + 5 q r3 + 2 r4)
T2 = b4 (-8 p4 – 12 p3 q – 3 p2 q2 – 2 p q3 – 3 q4 + 4 p3 r + 18 p2 q r + 12 p q2 r – 2 q3 r – 3 p2 r2 + 18 p q r2 – 3 q2 r2 + 4 p r3 – 12 q r3 – 8 r4) +
a4 (-3 p4 – 2 p3 q – 3 p2 q2 – 12 p q3 – 8 q4 – 2 p3 r + 12 p2 q r + 18 p q2 r + 4 q3 r – 3 p2 r2 + 18 p q r2 – 3 q2 r2 – 12 p r3 + 4 q r3 – 8 r4) +
c4 (-8 p4 + 4 p3 q – 3 p2 q2 + 4 p q3 – 8 q4 – 12 p3 r + 18 p2 q r + 18 p q2 r – 12 q3 r – 3 p2 r2 + 12 p q r2 – 3 q2 r2 – 2 p r3 – 2 q r3 – 3 r4) +
2 b2 c2 (4 p3 q + 3 p2 q2 + 3 p q3 + 4 q4 + 4 p3 r – 18 p2 q r – 3 p q2 r + q3 r + 3 p2 r2 – 3 p q r2 – 6 q2 r2 + 3 p r3 + q r3 + 4 r4) +
2 a2 b2 (4 p4 + p3 q – 6 p2 q2 + p q3 + 4 q4 + 3 p3 r – 3 p2 q r – 3 p q2 r + 3 q3 r + 3 p2 r2 – 18 p q r2 + 3 q2 r2 + 4 p r3 + 4 q r3) +
2 a2 c2 (4 p4 + 3 p3 q + 3 p2 q2 + 4 p q3 + p3 r – 3 p2 q r – 18 p q2 r + 4 q3 r – 6 p2 r2 – 3 p q r2 + 3 q2 r2 + p r3 + 3 q r3 + 4 r4)
Properties
- QA-P1 lies on QA-L10.
- There is no line with largest sum of squared distances. However when we look for the line with this property passing through QA-P1, then QA-L10p being the line through QA-P1 perpendicular to QA-L10 will be the line with largest sum of squared distances.
- In a Quadrilateral the triangle formed by the 3 QL-versions of QA-L10 and the triangle formed by the 3 QL-versions of QA-L10p are perspective in a common point of the circumscribed circles of these triangles.
Estimated human page views: 713
