QA-P44 Least Squared Distance Point of QA-sidelines

QA-P44 is the point with the Least Sum of Squared Distances to the six sidelines of a Quadrangle.

For a discussion on this point see [34], QFG-messages #13, #1569 and following messages.

Construction:

The point can be constructed in a similar way as described in the 1^st construction of QL-P26 according to [25].

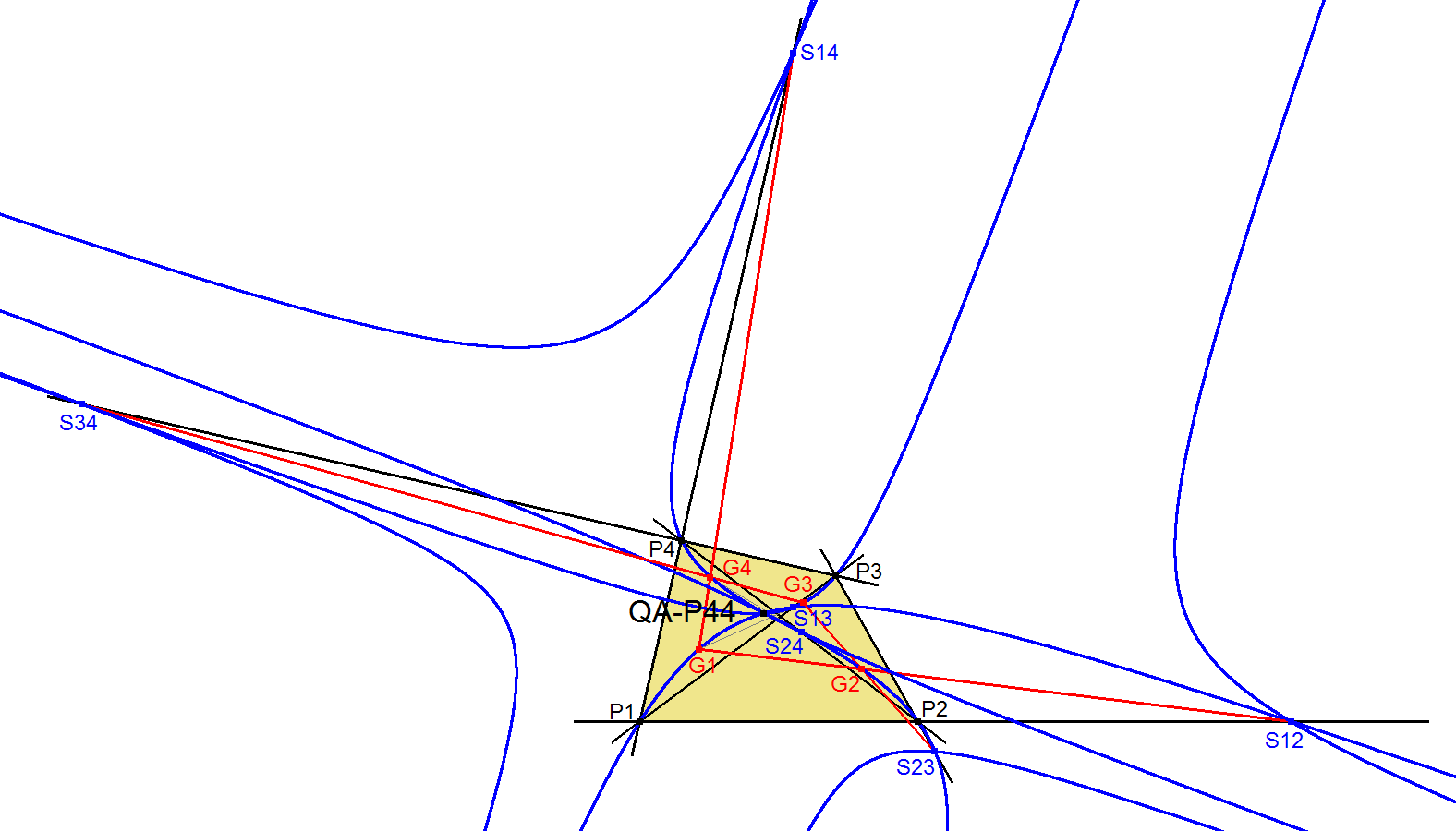
Another construction (see [34], QFG-message #1589):

• Let P1, P2, P3, P4 be the 4 defining points of the Reference Quadrangle QA.
• Let Gi be the Centroid of the orthogonal projection points of Pi on the 6 sidelines of QA.
• Let Sij=Pi.Pj^Gi.Gj for all combinations i=1,2,3,4, j=1,2,3,4, i<>j.
• Let Coi=Conic(Pi,Gi,Sij,Sik,Sil), where i,j,k,l have different values from (1,2,3,4).
• This delivers the 4 conics Co1, Co2, Co3, Co4 with common point QA-P44.
• Moreover these conics are orthogonal hyperbolas with 4 sets of parallel asymptotes.

1st CT-Coordinate

a⁶ q² (p + q) r² (p + r)

+c⁶ p² q² (p + r) (3 q + 2 r)

+b⁶ p² (p + q) r² (2 q + 3 r)

-b⁴ c² p² r (4 p² q – 4 q³ + 6 p² r + 9 p q r + 2 q² r + 6 p r² + 7 q r²)

-b² c⁴ p² q (6 p² q + 6 p q² + 4 p² r + 9 p q r + 7 q² r + 2 q r² – 4 r³)

+a⁴ c² q² r (p + r) (2 p² – 2 q² – 2 p r – q r)

+a⁴ b² q (p + q) r² (2 p² – 2 p q – q r – 2 r²)

-a² c⁴ p q² (p + r) (3 p q + 3 q² + 4 p r – r²)

-a² b⁴ p (p + q) r² (4 p q – q² + 3 p r + 3 r²)

+2 a² b² c² p q r (2 p³ – p² q – 2 p q² + q³ – p² r – 4 p q r – 3 q² r – 2 p r² – 3 q r² + r³)

The sum of squared distances for QA-P44 is:

((-a + b + c) (a + b – c) (a – b + c) (a + b + c) (-6 b² c⁴ p⁴ q² – 3 a² c⁴ p³ q³ – 3 b² c⁴ p³ q³ + 3 c⁶ p³ q³ – 6 a² c⁴ p² q⁴ + 4 a² b² c² p⁴ q r – 4 b⁴ c² p⁴ q r – 4 b² c⁴ p⁴ q r + 2 a⁴ c² p³ q² r – 4 a² b² c² p³ q² r + 2 b⁴ c² p³ q² r – 4 a² c⁴ p³ q² r – 4 b² c⁴ p³ q² r + 2 c⁶ p³ q² r + 2 a⁴ c² p² q³ r – 4 a² b² c² p² q³ r + 2 b⁴ c² p² q³ r – 4 a² c⁴ p² q³ r – 4 b² c⁴ p² q³ r + 2 c⁶ p² q³ r – 4 a⁴ c² p q⁴ r + 4 a² b² c² p q⁴ r – 4 a² c⁴ p q⁴ r – 6 b⁴ c² p⁴ r² + 2 a⁴ b² p³ q r² – 4 a² b⁴ p³ q r² + 2 b⁶ p³ q r² – 4 a² b² c² p³ q r² – 4 b⁴ c² p³ q r² + 2 b² c⁴ p³ q r² + a⁶ p² q² r² – a⁴ b² p² q² r² – a² b⁴ p² q² r² + b⁶ p² q² r² – a⁴ c² p² q² r² – 12 a² b² c² p² q² r² – b⁴ c² p² q² r² – a² c⁴ p² q² r² – b² c⁴ p² q² r² + c⁶ p² q² r² + 2 a⁶ p q³ r² – 4 a⁴ b² p q³ r² + 2 a² b⁴ p q³ r² – 4 a⁴ c² p q³ r² – 4 a² b² c² p q³ r² + 2 a² c⁴ p q³ r² – 6 a⁴ c² q⁴ r² – 3 a² b⁴ p³ r³ + 3 b⁶ p³ r³ – 3 b⁴ c² p³ r³ + 2 a⁴ b² p² q r³ – 4 a² b⁴ p² q r³ + 2 b⁶ p² q r³ – 4 a² b² c² p² q r³ – 4 b⁴ c² p² q r³ + 2 b² c⁴ p² q r³ + 2 a⁶ p q² r³ – 4 a⁴ b² p q² r³ + 2 a² b⁴ p q² r³ – 4 a⁴ c² p q² r³ – 4 a² b² c² p q² r³ + 2 a² c⁴ p q² r³ + 3 a⁶ q³ r³ – 3 a⁴ b² q³ r³ – 3 a⁴ c² q³ r³ – 6 a² b⁴ p² r⁴ – 4 a⁴ b² p q r⁴ – 4 a² b⁴ p q r⁴ + 4 a² b² c² p q r⁴ – 6 a⁴ b² q² r⁴)) /

(4 (-6 a² b² c⁴ p⁴ q² – 3 b⁴ c⁴ p⁴ q² – 2 b² c⁶ p⁴ q² – 3 a⁴ c⁴ p³ q³ – 12 a² b² c⁴ p³ q³ – 3 b⁴ c⁴ p³ q³ + 2 a² c⁶ p³ q³ + 2 b² c⁶ p³ q³ + c⁸ p³ q³ – 3 a⁴ c⁴ p² q⁴ – 6 a² b² c⁴ p² q⁴ – 2 a² c⁶ p² q⁴ + 4 a⁴ b² c² p⁴ q r – 2 a² b⁴ c² p⁴ q r – 2 b⁶ c² p⁴ q r – 2 a² b² c⁴ p⁴ q r – 6 b⁴ c⁴ p⁴ q r – 2 b² c⁶ p⁴ q r + 2 a⁶ c² p³ q² r + 2 a⁴ b² c² p³ q² r – 4 a² b⁴ c² p³ q² r – 3 a⁴ c⁴ p³ q² r – 22 a² b² c⁴ p³ q² r – 3 b⁴ c⁴ p³ q² r + 2 b² c⁶ p³ q² r + c⁸ p³ q² r – 4 a⁴ b² c² p² q³ r + 2 a² b⁴ c² p² q³ r + 2 b⁶ c² p² q³ r – 3 a⁴ c⁴ p² q³ r – 22 a² b² c⁴ p² q³ r – 3 b⁴ c⁴ p² q³ r + 2 a² c⁶ p² q³ r + c⁸ p² q³ r – 2 a⁶ c² p q⁴ r – 2 a⁴ b² c² p q⁴ r + 4 a² b⁴ c² p q⁴ r – 6 a⁴ c⁴ p q⁴ r – 2 a² b² c⁴ p q⁴ r – 2 a² c⁶ p q⁴ r – 6 a² b⁴ c² p⁴ r² – 2 b⁶ c² p⁴ r² – 3 b⁴ c⁴ p⁴ r² + 2 a⁶ b² p³ q r² – 3 a⁴ b⁴ p³ q r² + b⁸ p³ q r² + 2 a⁴ b² c² p³ q r² – 22 a² b⁴ c² p³ q r² + 2 b⁶ c² p³ q r² – 4 a² b² c⁴ p³ q r² – 3 b⁴ c⁴ p³ q r² + a⁸ p² q² r² + 2 a⁶ b² p² q² r² – 6 a⁴ b⁴ p² q² r² + 2 a² b⁶ p² q² r² + b⁸ p² q² r² + 2 a⁶ c² p² q² r² – 12 a⁴ b² c² p² q² r² – 12 a² b⁴ c² p² q² r² + 2 b⁶ c² p² q² r² – 6 a⁴ c⁴ p² q² r² – 12 a² b² c⁴ p² q² r² – 6 b⁴ c⁴ p² q² r² + 2 a² c⁶ p² q² r² + 2 b² c⁶ p² q² r² + c⁸ p² q² r² + a⁸ p q³ r² – 3 a⁴ b⁴ p q³ r² + 2 a² b⁶ p q³ r² + 2 a⁶ c² p q³ r² – 22 a⁴ b² c² p q³ r² + 2 a² b⁴ c² p q³ r² – 3 a⁴ c⁴ p q³ r² – 4 a² b² c⁴ p q³ r² – 2 a⁶ c² q⁴ r² – 6 a⁴ b² c² q⁴ r² – 3 a⁴ c⁴ q⁴ r² – 3 a⁴ b⁴ p³ r³ + 2 a² b⁶ p³ r³ + b⁸ p³ r³ – 12 a² b⁴ c² p³ r³ + 2 b⁶ c² p³ r³ – 3 b⁴ c⁴ p³ r³ – 3 a⁴ b⁴ p² q r³ + 2 a² b⁶ p² q r³ + b⁸ p² q r³ – 4 a⁴ b² c² p² q r³ – 22 a² b⁴ c² p² q r³ + 2 a² b² c⁴ p² q r³ – 3 b⁴ c⁴ p² q r³ + 2 b² c⁶ p² q r³ + a⁸ p q² r³ + 2 a⁶ b² p q² r³ – 3 a⁴ b⁴ p q² r³ – 22 a⁴ b² c² p q² r³ – 4 a² b⁴ c² p q² r³ – 3 a⁴ c⁴ p q² r³ + 2 a² b² c⁴ p q² r³ + 2 a² c⁶ p q² r³ + a⁸ q³ r³ + 2 a⁶ b² q³ r³ – 3 a⁴ b⁴ q³ r³ + 2 a⁶ c² q³ r³ – 12 a⁴ b² c² q³ r³ – 3 a⁴ c⁴ q³ r³ – 3 a⁴ b⁴ p² r⁴ – 2 a² b⁶ p² r⁴ – 6 a² b⁴ c² p² r⁴ – 2 a⁶ b² p q r⁴ – 6 a⁴ b⁴ p q r⁴ – 2 a² b⁶ p q r⁴ – 2 a⁴ b² c² p q r⁴ – 2 a² b⁴ c² p q r⁴ + 4 a² b² c⁴ p q r⁴ – 2 a⁶ b² q² r⁴ – 3 a⁴ b⁴ q² r⁴ – 6 a⁴ b² c² q² r⁴))

Properties

• QA-P44 is also the Centroid of the orthogonal projection points of QA-P44 on the six sidelines.

Estimated human page views: 511