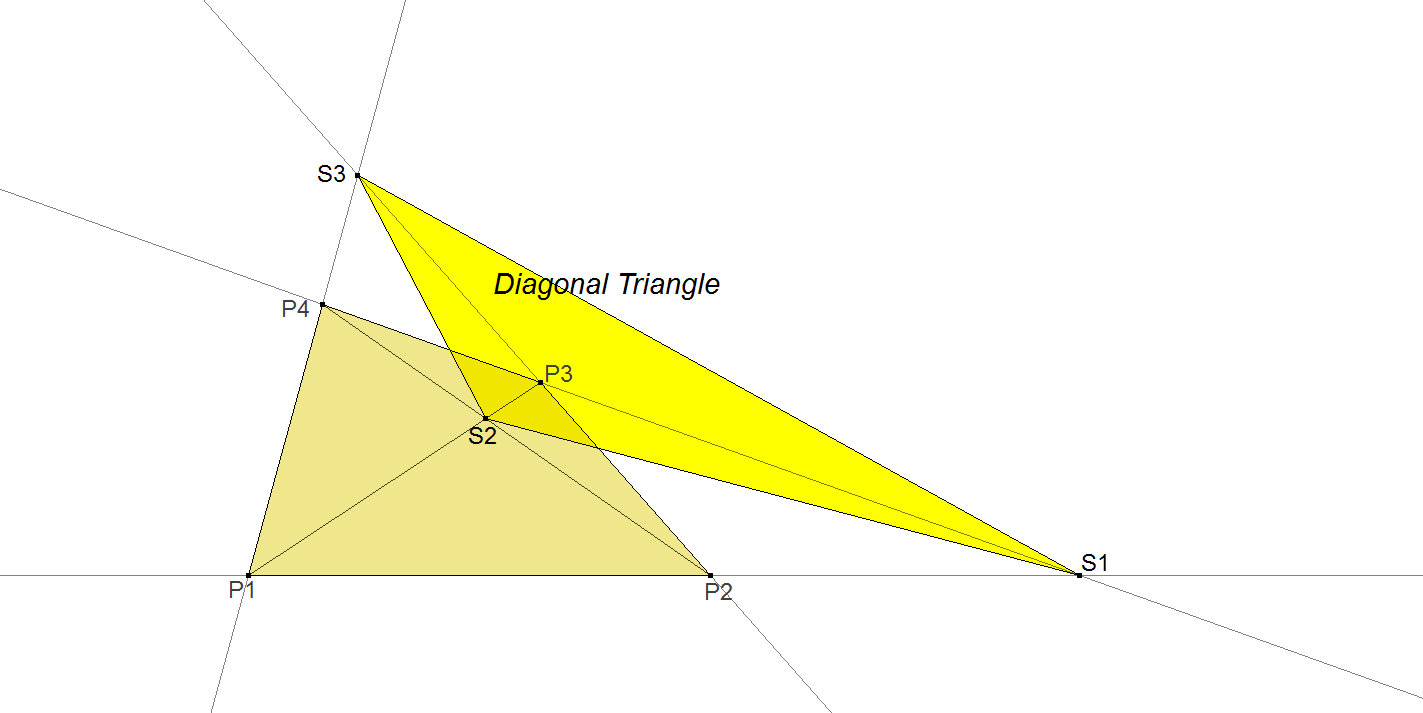
QA-Tr1: QA-Diagonal Triangle

Let P1, P2, P3, P4 be the defining Quadrangle Points.

Let S1 = P1.P2 ^ P3.P4, S2 = P1.P3 ^ P2.P4 and S3 = P1.P4 ^ P2.P3.

Now S1.S2.S3 is the QA-Diagonal Triangle of the Reference Quadrangle.

Area QA-Diagonal Triangle in CT-notation:

2 p q r Δ / ((p + q) (p + r) (q + r))

Area QA-Diagonal Triangle in DT-notation:

2 S

Properties

• Every Component Triangle Pi.Pj.Pk is the Anticevian Triangle of the 4^th point Pl (for all combinations of (i,j,k,l) ∈ (1,2,3,4)).
• The vertices of the QA-Diagonal Triangle combined with the Isotomic Center form a new quadrangle with the same QA-Centroid as the Reference Quadrangle.
• The Isogonal Center of the Quadrangle S1.S2.S3.QA-P4 is the Involutary Conjugate of QA-P4 (note Eckart Schmidt).
• QA-Tr1 is self-polar wrt every conic circumscribing the Reference Quadrangle. See [11], Hyacinthos message #15520.

Estimated human page views: 609