QL-12L1: A dozen of Equidistance Lines
There is the general question of constructing a line in a quadrilateral (a system of 4 lines) such that this line is divided by the 4 lines in 3 equal parts.
This problem is dealt with at [14] Philippe Chevanne, Mad Maths, Recreational mathematic collection.
Also a simple synthetic solution is given.
In this paper the 12 algebraically solutions will be given in QL-notation.
The next picture illustrates how these solutions look like in a square-situation.
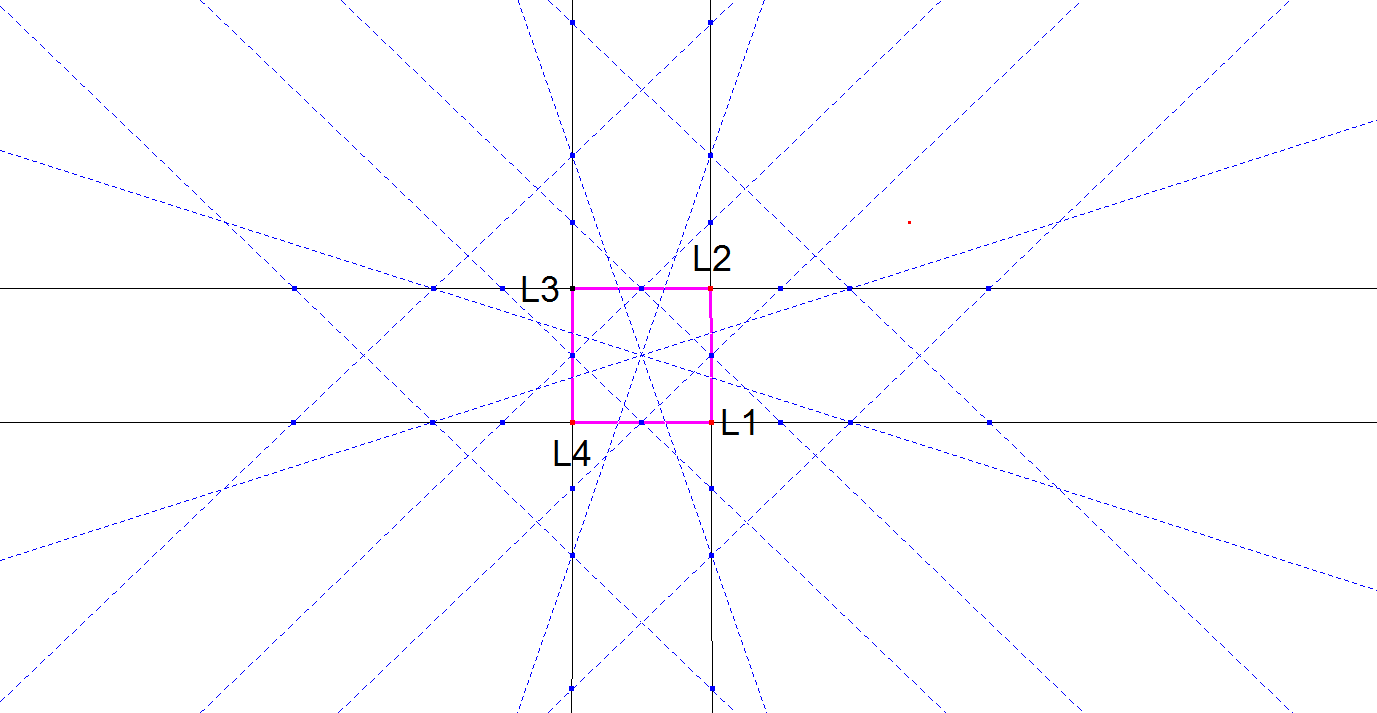
All dotted lines are Equidistance Lines and are divided by the 4 bounding lines of the square in equal parts.
When choosing random basic lines for the Reference Quadrilateral it looks like this:
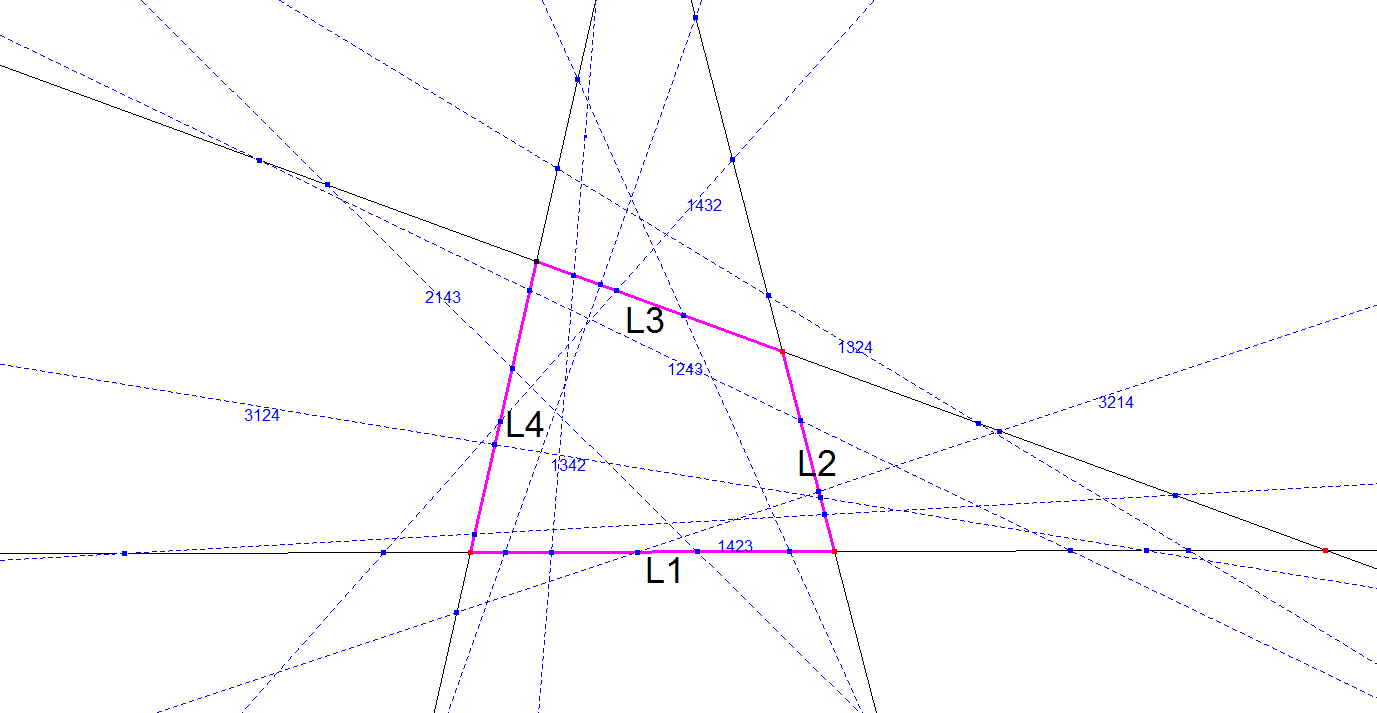
We can split up the dozen equidistance lines per quadrigon of the quadrilateral.
In each quadrigon 4 equidistance lines occur where each middle splitted part of the equidistance line is a line segment between 2 opposite lines of the quadrigon.
In next figure quadrigon L1.L2.L3.L4 is shown with its 4 equidistance lines.
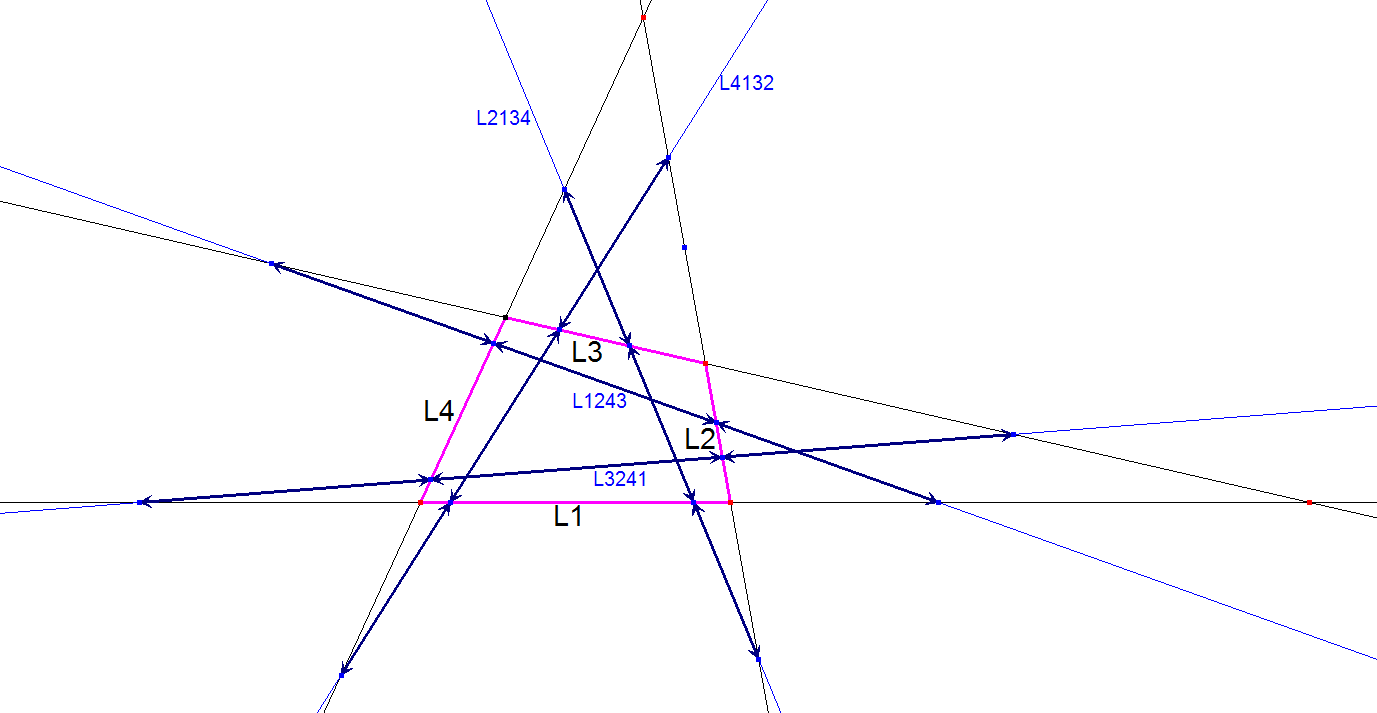
Accordingly each equidistance line can be ascribed to 1 of the 3 component quadrigons:
| Quadrigon L1.L2.L3.L4 | Quadrigon L1.L3.L2.L4 | Quadrigon L1.L2.L4.L3 | |
|---|---|---|---|
| Equidistance Line | L4132 | L3124 | L2143 |
| Equidistance Line | L2134 | L4123 | L3142 |
| Equidistance Line | L3241 | L1342 | L1234 |
| Equidistance Line | L1243 | L2341 | L4231 |
Note 1:
L4132 indicates the equidistance line intersecting QL-lines in order L4, L1, L3, L2.
Note 2:
The two middle line numbers per equidistance line in the table are opposite lines in the quadrigons in which they occur.
Coefficients of the 12 lines as well as their 12 Midpoints (see also QL-12P1)
The infinity points of the Equidistance Lines (indicating their direction) are important in this setting and have simple coordinates. These coordinates are actually the building blocks of the Equidistance Line itself and its Midpoint as will be shown in next tables.
Next all mentioned coordinates will be CT-coordinates.
EquiDistance Lines in Quadrigon L1.L2.L3.L4
| L2134 | L4132 | L1243 | L3241 | |
|---|---|---|---|---|
| Infinity Point EquiDistance Line | (x : y : z) | (x : y : z) | (x : y : z) | (x : y : z) |
| where: | x = 3m – n | x = 3m – 2n | x = –m – n | x = +m – 2n |
| y = n – 2l | y = 2n – l | y = +n + 2l | y = +2n + l | |
| z = 2l – 3m | z = l – 3m | z = –2l + m | z = –l – m | |
| EquiDistance Line | (–2/x : 1/y : 1/z) | (1/x : 1/y : –2/z) | (2/x : –3/y : 1/z) | (1/x : –3/y : 2/z) |
| EquiDistance Midpoint | (x : 3y : –z) | (x : –3y : –z) | (x : y/3 : –z) | (x : –y/3 : –z) |
EquiDistance Lines in Quadrigon L1.L3.L2.L4
| L3124 | L4123 | L2341 | L1342 | |
|---|---|---|---|---|
| Infinity Point EquiDistance Line | (x : y : z) | (x : y : z) | (x : y : z) | (x : y : z) |
| where: | x = m – 3n | x = 2m – 3n | x = 2m – n | x = –m – n |
| y = –3n + 2l | y = 3n – l | y = n + l | y = n – 2l | |
| z = –2l + m | z = l – 2m | z = –l – 2m | z = 2l + m | |
| EquiDistance Line | (–2/x : 1/y : 1/z) | (1/x : –2/y : 1/z) | (1/x : 2/y : –3/z) | (2/x : 1/y : –3/z) |
| EquiDistance Midpoint | (x : –y : 3z) | (x : –y : –3z) | (x : –y : –z/3) | (x : –y : z/3) |
EquiDistance Lines in Quadrigon L1.L2.L4.L3
| L2143 | L3142 | L1234 | L4231 | |
|---|---|---|---|---|
| Infinity Point EquiDistance Line | (x : y : z) | (x : y : z) | (x : y : z) | (x : y : z) |
| where: | x = 2m + n | x = m + 2n | x = 2m – n | x = –m – 2n |
| y = –n – l | y = –2n + l | y = n – 3l | y = 2n – 3l | |
| z = l – 2m | z = –l – m | z = 3l – 2m | z = 3l – m | |
| EquiDistance Line | (–3/x : 2/y : 1/z) | (–3/x : 1/y : 2/z) | (1/x : –2/y : 1/z) | (1/x : 1/y : –2/z) |
| EquiDistance Midpoint | (x/3 : y : –z) | (–x/3 : y : –z) | (3x : y : –z) | (–3x : y : –z) |
Properties
- The Involutary Conjugate (QA-Tf2) of the Infinity Point of an Equidistance Line (performed in the Quadrigon where the Equidistance Line is constructed) coincides with the Equidistance Midpoint (see QL-12P1) on this line.
- The center of the Circumscribed Hyperbola through P1, P2, P3, P4 and the Infinity Point of an Equidistance Line is the 2nd intersection point of this Equidistance Line and the Nine-point Conic (QA-Co1) of the Reference Quadrigon.
Estimated human page views: 504
