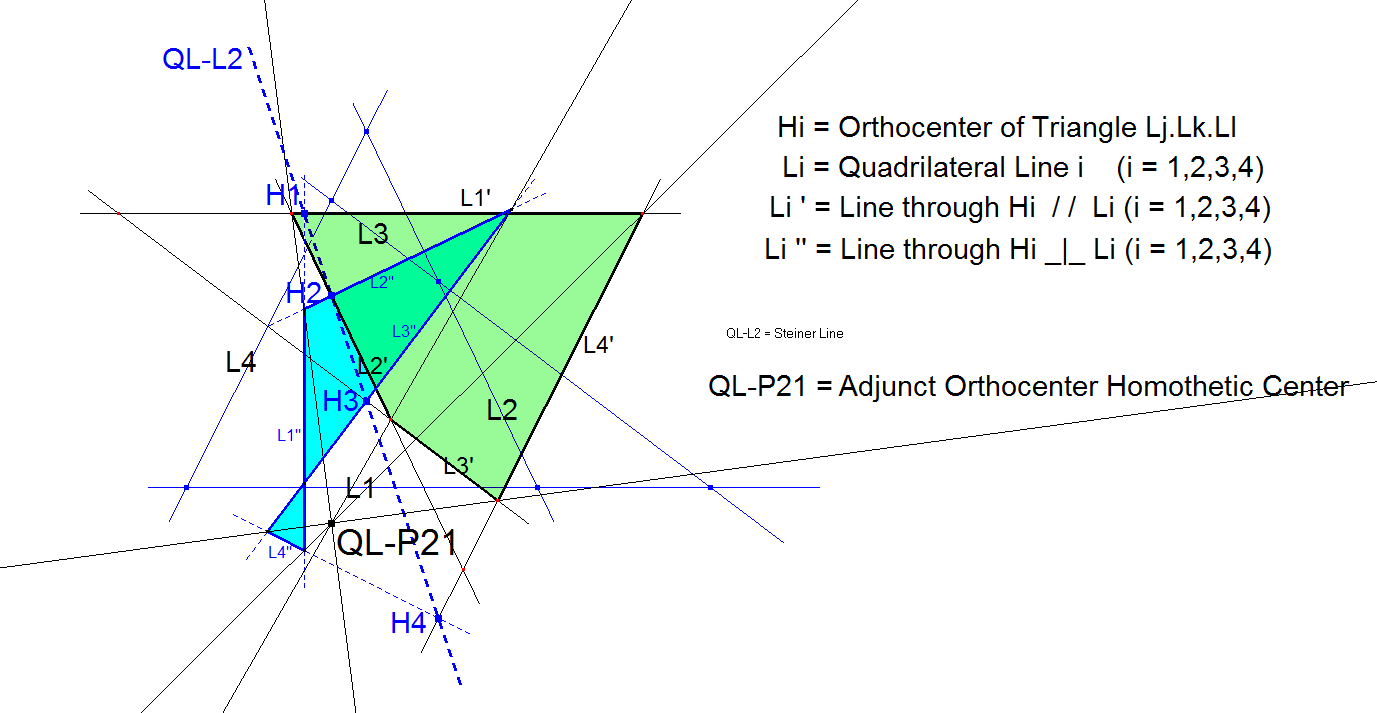
QL-P21: Adjunct Orthocenter Homothetic Center
QL-P21 is the Perspector of
the Quadrilateral formed by the lines parallel to the lines L1, L2, L3, L4 through the Orthocenters of the corresponding component triangles and
the Quadrilateral formed by the lines perpendicular to the lines L1, L2, L3, L4 through the Orthocenters of the corresponding component triangles.
1st CT-Coordinate
2 a2 (a4 + (b2 – c2)2 – 2 a2 (b2 + c2)) (l – m)2 m (l – n)2 (m – n) n
+ 2(-m + n) (a2 m n (l – m) (l – n) + b2 l n (m – l) (m – n) + c2 l m (n – l) (n – m)) (2 a2 (b2 m (l – n) + c2 n (l – m))
+ a4 (-l2 + m n) + (b2 – c2)(b2 (l2 – 2 l m + m n) – c2 (l2 – 2 l n + m n)))
1st DT-coordinate
Tl (Sa3 Tl4 + Sb3 Tm4 + Sc3 Tn4
+ 2 (m2 + n2) Sa Sb Sc Tm Tn (Tn – Tm)
+ Sa2 Tl2 ((m2 + 3 n2) Sb Tm – (3 m2 + n2) Sc Tn)
+ Sc2 Tn2 (Sb Tm (Tl + 3 Tm) + Sa (3 l2 Tl – 2 n2 Tl – 3 m2 Tn + m2 Tm))
+ Sb2 Tm2 (Sc Tn (Tl + 3 Tn) + Sa (3 n2 Tm + 2 m2 Tl – 3 l2 Tl – n2 Tn)))
where: Tl = m2 – n2 Tm = n2 – l2 Tn = l2 – m2
Properties
- QL-P21 lies on this line:
- QL-P21 lies on the asymptote of the cubic QL-Cu1.
- QL-P21 and QL-P1 lie at different sides from QL-L1 (Newton Line) with same distances to QL-L1.
Estimated human page views: 597
