7P-s-Tf1 7P-CB Conjugate
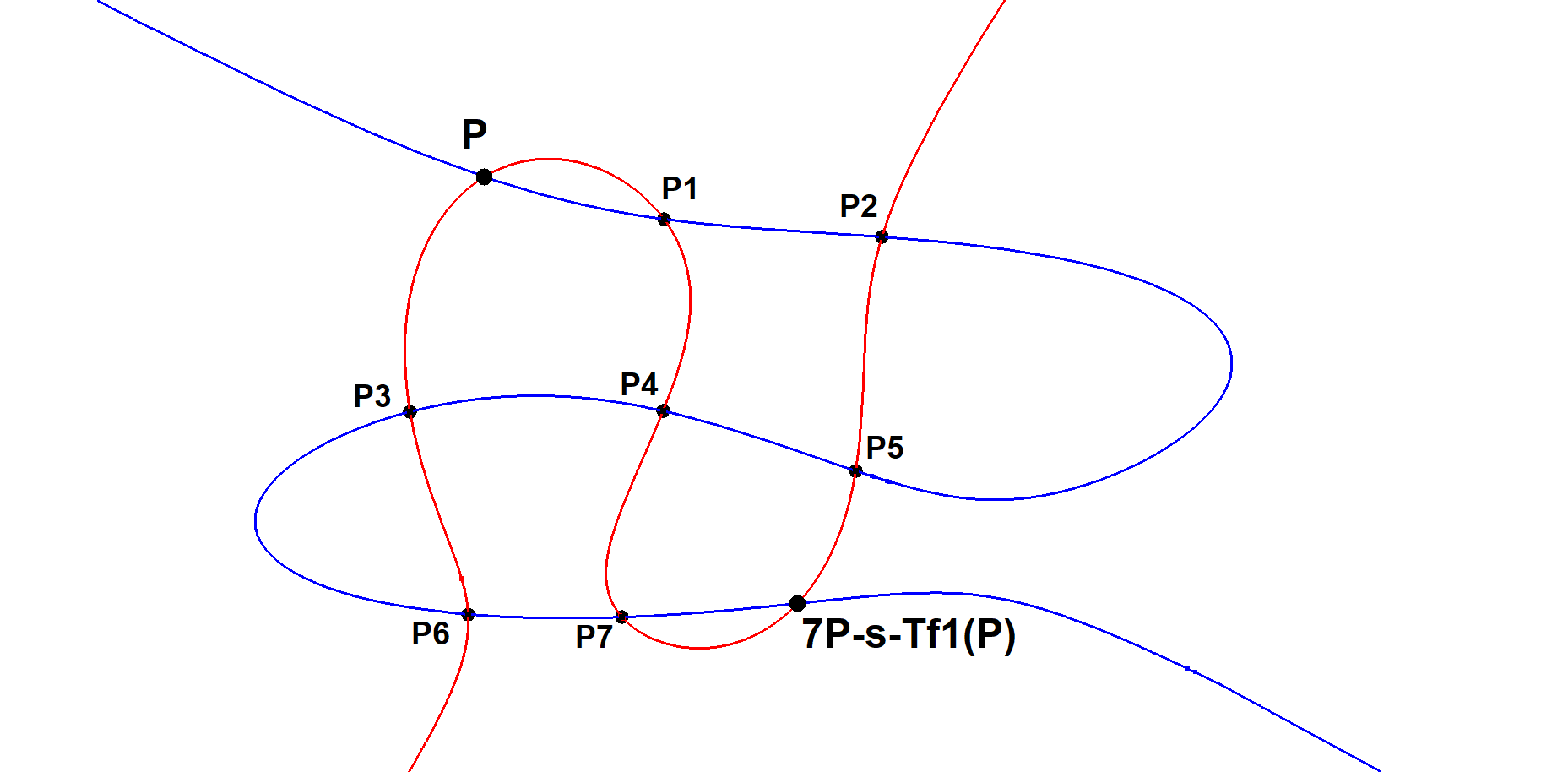
A cubic (9P-s-Cu1) is determined by 9 points. Through 8 random points infinitely many cubics can be drawn. However according to the Cayley-Bacharach theorem they all pass through a common point, named the Cayley-Bacharach point (8P-s-P1). Therefore a Heptangle (7 points) and an extra random point P (+1 point) will determine a Cayley-Bacharach point, which is 7P-s-Tf1(P).
Note that the abbreviation “CB” is spelled here with capitals, in contrast to the corresponding cb Conjugate 5P-s-Tf6(P), where the abbreviation “cb” is spelled with lower-case letters.
Construction
Take the 7 points of the 7P (Heptangle) and the extra 8th point and use the construction of 8P-s-P1.
Properties
- 7P-s-Tf1(7P-s-Tf1(P)) = P
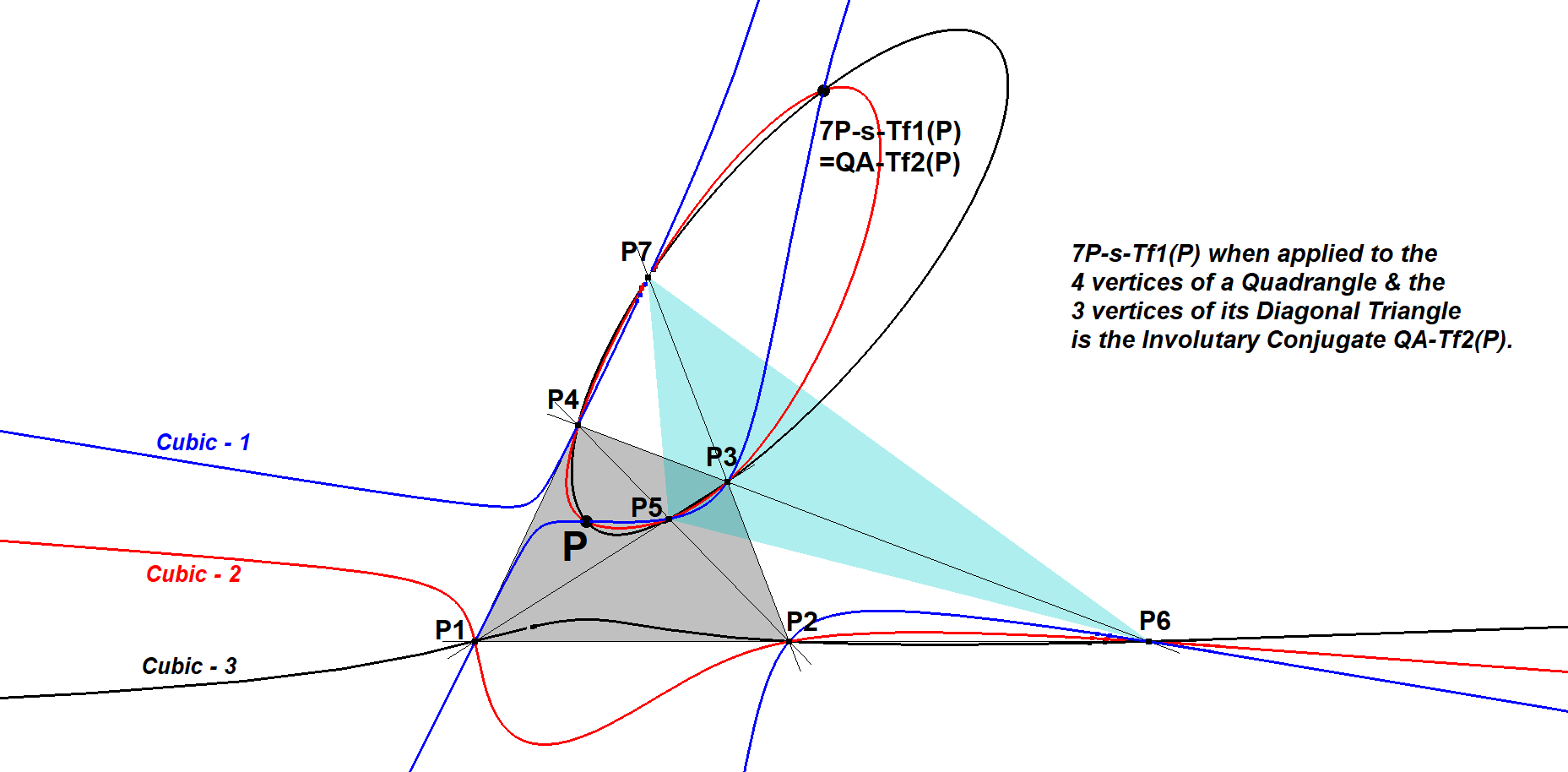
- Let P1P2P3P4 be a quadrangle and let P5P6P7 be its diagonal triangle and P is some random point, then 7P-s-Tf1(P) = QA-Tf2(P). See [34], Seiichi Kirikami, QFG#1698.
Estimated human page views: 239
