← Previous Next →

8P-s-P1: Cayley Bacharach Point

The Cayley-Bacharach Point in an Octangle is defined as follows:

Let P1,…,P8 be eight distinct points in the plane, no four of which collinear, and no seven of them on a conic. There exists a unique ninth point P9 such that every cubic curve through P1,…,P8 also contains P9.

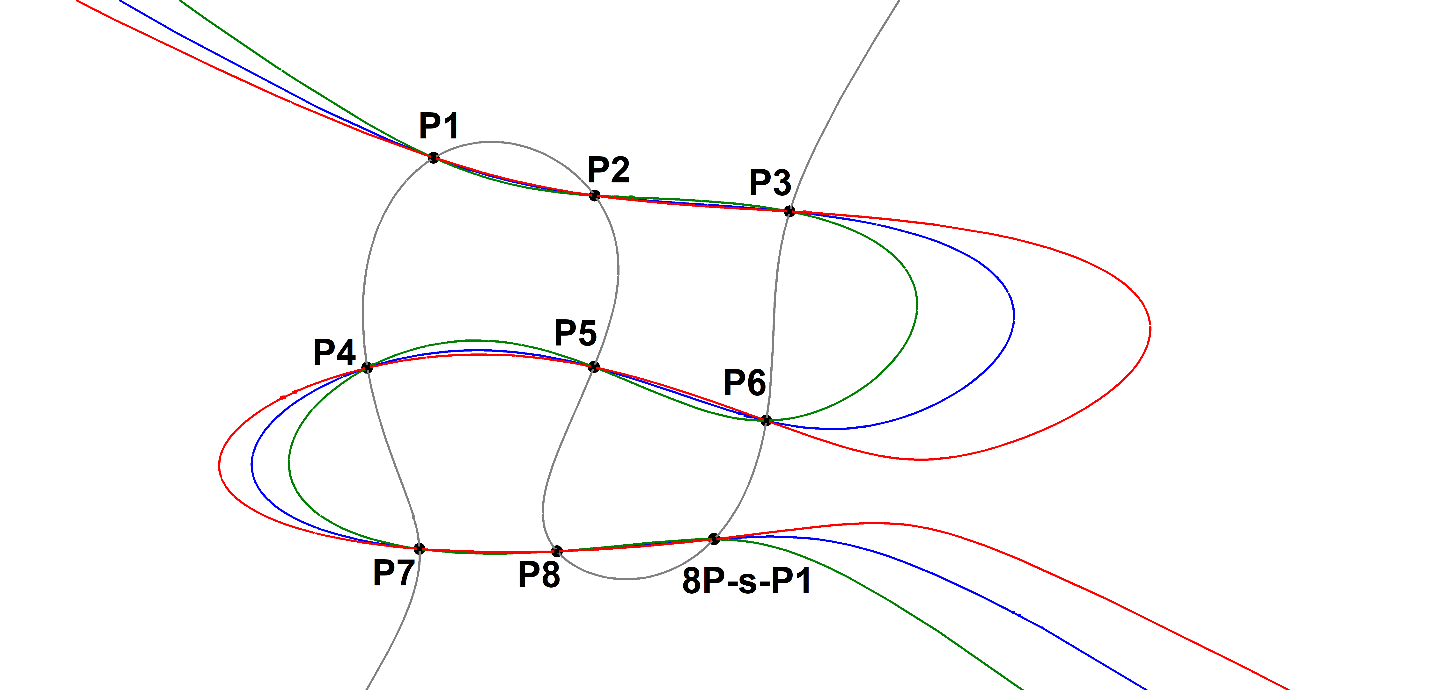
Infovisual 8P-s-P1-infovisual-cvt-01.png
Construction

A construction by the ruler alone of 8P-s-P1 is the method of A.S. Hart, which can be found at [64].

Many properties can be derived from the Cayley Bacharach Theorem, especially when a cubic is degenerated, for example in a conic and two lines, etc.

See also [34], QFG-messages #732, #733, #736, #737, #1476, #1491, #1517, #1696, #1698-1701, #1733.

Calculation

In [69] is given a method for calculating this point as follows:

  • Let P1 = (x1:y1:z1), P2 = (x2:y2:z2), etc.
  • Let C(P1,P2,P3,P4,P5,P6) = Determinant of
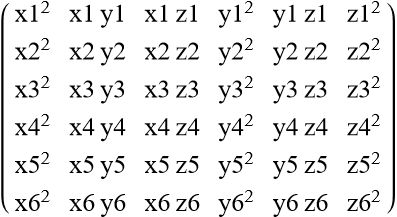
8P-s-P1-infovisual-cvt-02.png
  • Let D(P1;P2,P3,P4,P5,P6,P7,P8) = Determinant of
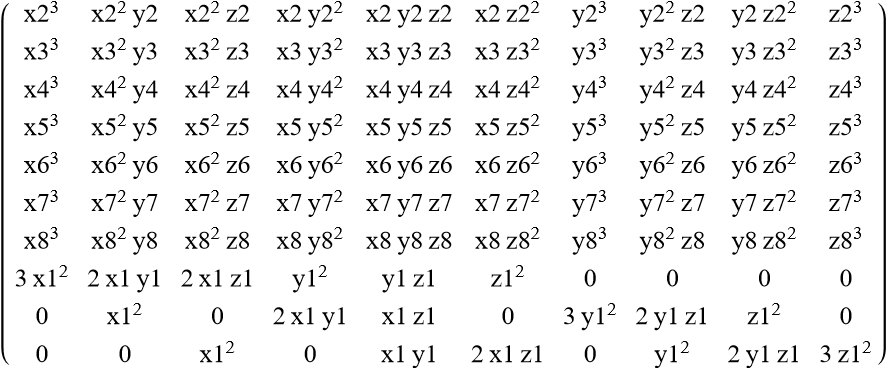
8P-s-P1-infovisual-cvt-03.png
  • Define:
  • Cx = C(P1,P4,P5,P6,P7,P8),
  • Cy = C(P2,P4,P5,P6,P7,P8),
  • Cz = C(P3,P4,P5,P6,P7,P8),
  • Dx = D(P1;P2,P3,P4,P5,P6,P7,P8),
  • Dy = D(P2;P3,P1,P4,P5,P6,P7,P8),
  • Dz = D(P3;P1,P2,P4,P5,P6,P7,P8).

Then the Cayley-Bacharach point CB is given by the formula:

CB = Cx Dy Dz · P1 + Dx Cy Dz · P2 + Dx Dy Cz · P3.

Correspondence with ETC/EQF

Eckart Schmidt wrote next properties of the Cayley Bacharach Point (CB-point) in relationship to Quadrangles/Quadrigons at [34], QFG#2640:

(1) Consider the vertices of a quadrangle and their complements wrt the remaining triangle.

The CB-point of these 8 points is QA-P1.

(2) Consider the vertices of a quadrangle and their anticomplements wrt the remaining triangle.

The CB-point of these 8 points is a new QA-point

… on a QA-circumscribed conic through QA-P10 and QA-P5

… and a parallel to QA-P1.QA-P16 through QA-P5,

… with tangent through QA-P16.

(3) Consider the vertices of a quadrangle and the in-/ex-centers of the Miquel triangle QA-Tr2.

The CB-point of these 8 points

… is the 3rd intersection of QA-Cu1 and Q.QA-P41

… with Q = intersection of QA-Cu1 and its asymptote (see EQF).

(4) Consider the vertices of a quadrangle and their isogonal conjugates wrt the Miquel triangle,

The CB-point of these 8 points is the tangential of Q wrt QA-Cu1.

(5) Consider the vertices of a quadrangle, its mid-DT and QA-P10.

The CB-point of these 8 points is the 2nd intersection of QA-P16.QA-P20 and the QA-circumconic through QA-P20.

(6) Consider the vertices of a quadrigon and the 4th parallelogram points of three consecutive vertices.

The CB-point of these 8 points is the reflection of QG-P1 in QG-P15.

(The QA-triangle of these CB-points is homothetic to QA-Tr1 wrt QA-P1 and factor -3.)

(7) Consider the vertices of QA-Tr1 and QA-Tr2 on QA-Cu1

… with Q and QA-P3: CB-point = QA-Tf2(res(QA-P4,QA-P41)) = QA-P41,

… with Q and QA-P4: CB-point = QA-Tf2(res(QA-P3,QA-P41)),

… with QA-P3 and QA-P4: CB-point = QA-Tf2(res(Q,QA-P41),

… with QA-P4 and QA-P41: CB-point = QA-Tf2(res(Q,QA-P3)).

Or: If you take the vertices of QA-Tr1 and QA-Tr2 and two of the points Q, QA-P3, QA-P4, QA-P41,

you get the CB-point as QA-Tf2-image of the 3rd intersection of QA-Cu1 and the line through the other two points.

(8) Consider the vertices of a quadrangle and Q, QA-P3, QA-P4, QA-P41.

The CB-point of these 8 points is res(Q,QA-Tf2(res(QA-P3,QA-P41))),

where res(X, Y) = 3rd intersection of QA-Cu1 and XY.

Other Properties
  • Let P1P2P3P4 be a quadrangle, P5P6P7 its diagonal triangle and P8 a random point, then the Cayley Bacharach Point will be the Involutary Conjugate of P8: QA-Tf2(P8). See [34], Seiichi Kirikami, QFG#1698.


Estimated human page views: 340

Scroll naar boven