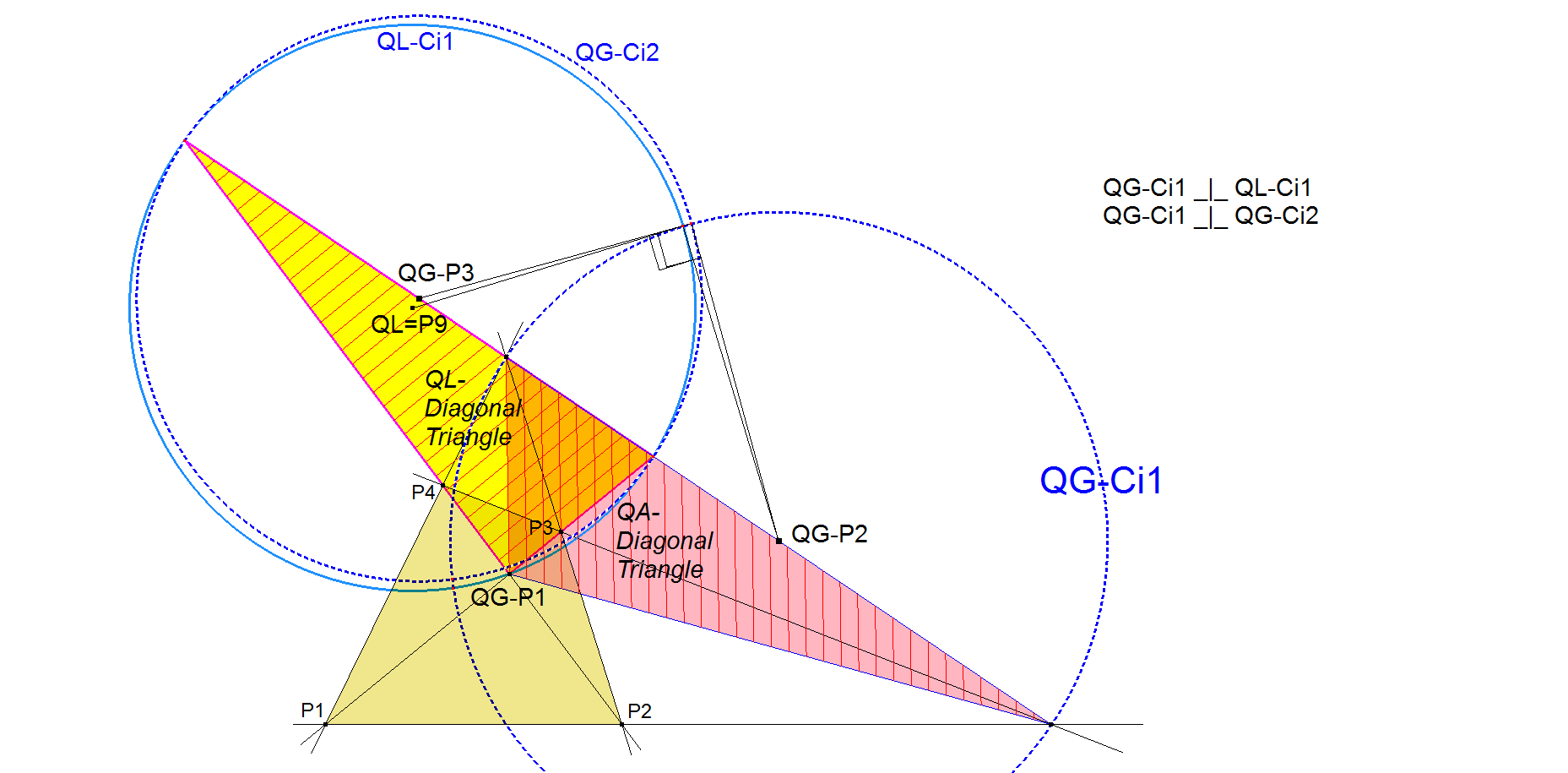
QG-Ci1: QA-DT-Thales Circle

The QA-DT-Thales Circle is the circle with the line segment between the vertices of the QA-Diagonal Triangle (QG-2P2a and QG-2P2b) that are unequal the Diagonal Crosspoint (QG-P1) as diameter.

CT-Equation QG-Ci1 in 1^st QA-Quadrigon:

q (2 c² q – a² r + b² r + c² r) x²

+ p r (a² – b² + c²) y²

+ q (a² p + b² p – c² p + 2 a² q) z²

+ (-2 c² p q + a² p r – b² p r – c² p r – a² q r + b² q r – c² q r) x y

+ (a² p q – b² p q – c² p q + 2 a² q² – 2 b² q² + 2 c² q² – 2 b² p r – a² q r – b² q r + c² q r) x z

+ (-a² p q + b² p q – c² p q – a² p r – b² p r + c² p r – 2 a² q r) y z = 0

CT-Equation QG-Ci1 in 1^st QL-Quadrigon:

-2 SA l x² + 2 SC n z² + (a² l – b² l + c² l – 2 c² n) x y + (a² l + b² l – c² l + a² n – b² n – c² n) x z

+ (2 a² l – a² n + b² n – c² n) y z = 0

DT-Equation QG-Ci1 in 1^st QA-Quadrigon:

(a² – b² + c²) x² + (a² – b² + 3 c²) x y + 2 (a² + c²) x z + (3 a² – b² + c²) y z + (a² – b² + c²) z² = 0

DT-Equation QG-Ci1 in 1^st QL-Quadrigon:

-b² l² x² – 2 SC l² x y – (a l – c n) (a l + c n) y² +2 SA n² y z + b² n² z² = 0

Properties

• QG-Ci1 is orthogonal wrt circles QG-Ci2 and QL-Ci1.
• The intersection points of QG-Ci1 with QG-Ci2 lie on the Perspective Squares Double Cubic QG-2Cu1.

Estimated human page views: 826