QG-P1

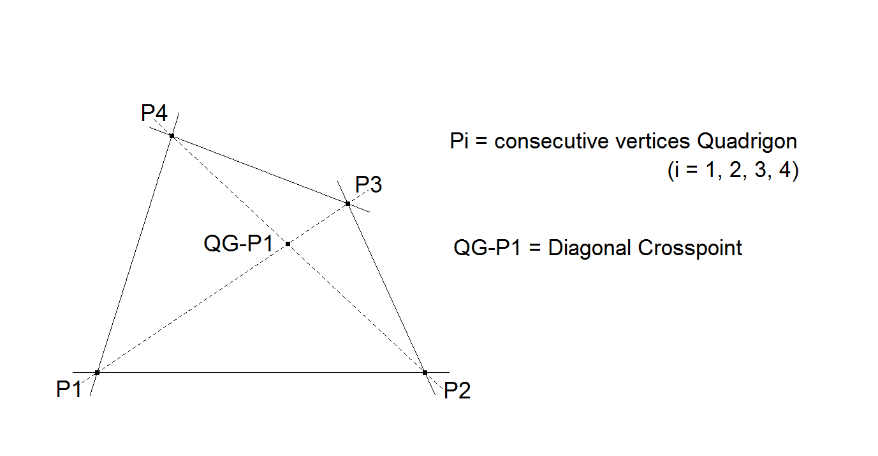
QG-P1: Diagonal Crosspoint

In a Quadrigon the vertices P1, P2, P3, P4 have a fixed order.

The Diagonal Crosspoint is the intersection point of the 2 lines connecting opposite points.

Four points can be ordened in 6 ways:

P1-P2-P3-P4
P1-P2-P4-P3
P1-P3-P2-P4
P1-P3-P4-P2 = reversed sequence of P1-P2-P4-P3
P1-P4-P2-P3 = reversed sequence of P1-P3-P2-P4
P1-P4-P3-P2 = reversed sequence of P1-P2-P3-P4

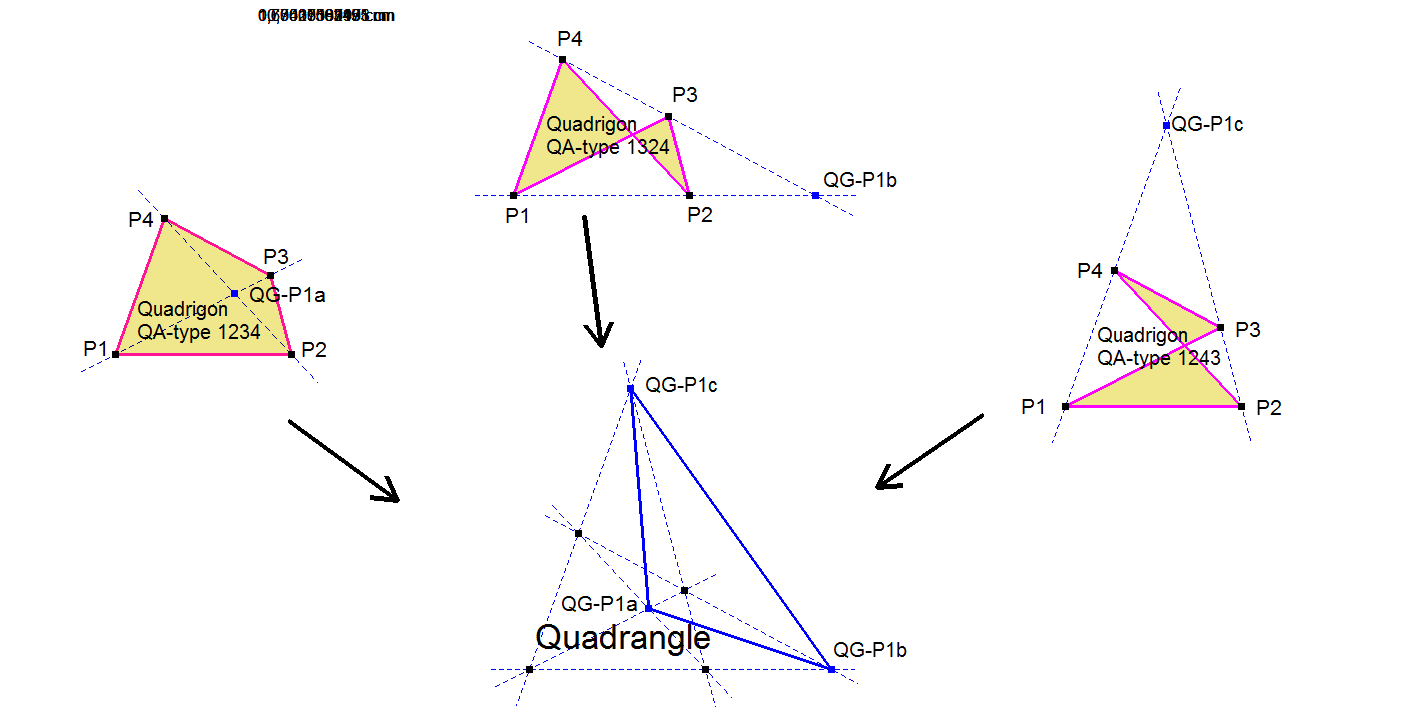
When we take into account that some sequences are reversed sequences, only 3 types of Quadrigon-orders remain: P1-P2-P3-P4, P1-P2-P4-P3 and P1-P3-P2-P4.

This means that a system of 4 points – also named (complete) quadrangle – consists of 3 quadrigons: P1-P2-P3-P4, P1-P2-P4-P3 and P1-P3-P2-P4.

These 3 quadrigons in a quadrangle produce different Diagonal Crosspoints as can be seen in next picture.

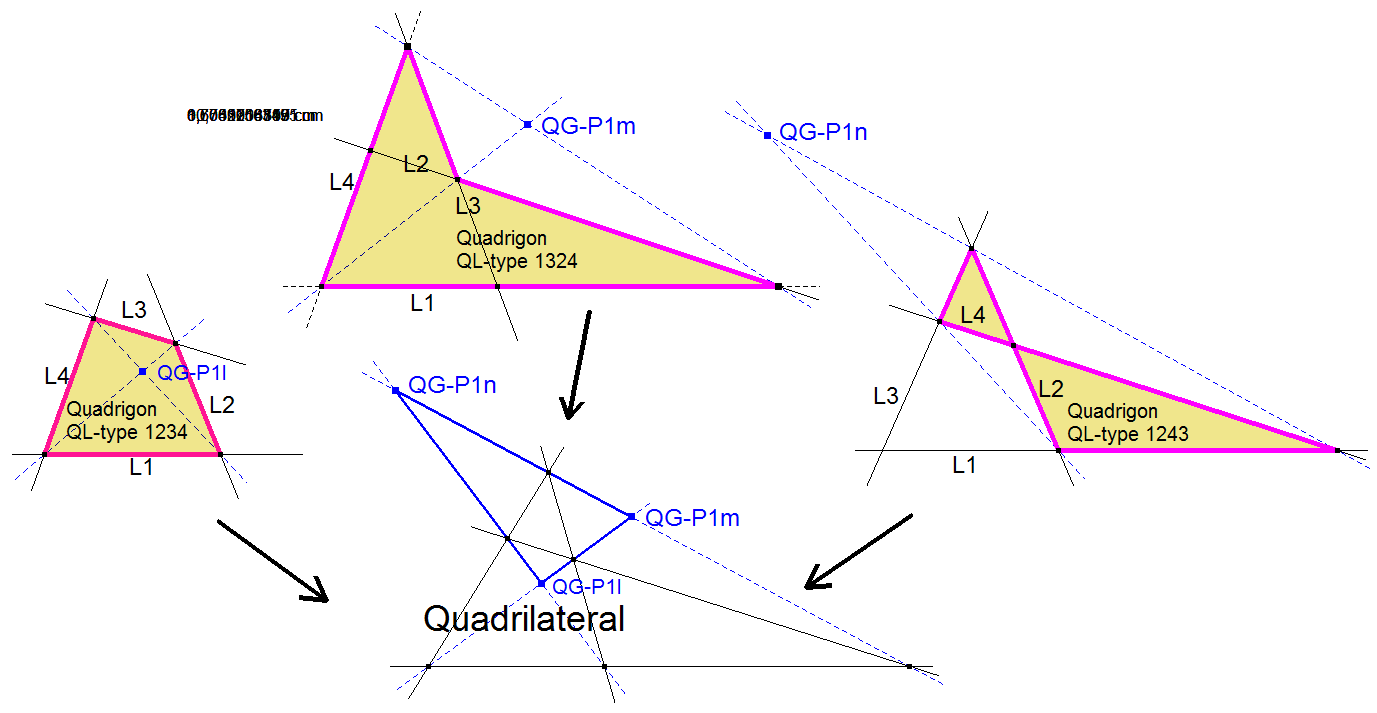
In the same way a system of 4 lines – also named (complete) quadrilateral – consists of 3 quadrigons: L1-L2-L3-L4, L1-L2-L4-L3 and L1-L3-L2-L4.

These 3 quadrigons in a quadrilateral produce different Diagonal Crosspoints as can be seen in next picture.

CT-Coordinates in 3 QA-Quadrigons

(p : q : 0), (0 : q : r) and (p : 0 : r)

CT-Coordinates in 3 QL-Quadrigons

(–m n : l n : l m), (m n : –l n : l m) and (m n : l n : –l m)

CT-Area of QG-P1–Triangle in the QA-environment

2 p q r Δ / ((p + q) (p + r) (q + r))= area QA-Diagonal Triangle

CT-Area of QG-P1–Triangle in the QL-environment

4 l² m² n² Δ / ((-l m + l n + m n) (l m + l n – m n) (l m – l n + m n))= area QL-Diagonal Triangle

—

DT-Coordinates in 3 QA-Quadrigons

(1 : 0 : 0), (0 : 1 : 0) and (0 : 0 : 1)

DT-Coordinates in 3 QL-Quadrigons

(1 : 0 : 0), (0 : 1 : 0) and (0 : 0 : 1)

DT-Area of QG-P1–Triangle in the QA-environment

S / 2

DT-Area of QG-P1–Triangle in the QL-environment

S / 2

Properties

The 3 Diagonal Crosspoints in a Quadrangle form the QA-Diagonal Triangle (see paragraph QA-Tr1: QA-Diagonal Triangle).
The 3 Diagonal Crosspoints in a Quadrilateral form the QL-Diagonal Triangle (see paragraph QL-Tr1: QL-Diagonal Triangle).
QG-P1 lies on these lines:
- QG-P4.QG-P8(2 : -1 = Reflection of QG-P4 in QG-P8)
- QG-P5.QG-P9(2 : -1 = Reflection of QG-P5 in QG-P9)
- QG-P6.QG-P10(2 : -1 = Reflection of QG-P6 in QG-P10)
- QG-P7.QG-P11(2 : -1 = Reflection of QG-P7 in QG-P11)
- QG-P15.QA-P1(2 : -1 = Reflection of QG-P15 in QA-P1)
- QG-P12.QG-P13
- QL-P8.QG-P3(-2 : 3 = QL-AntiComplement of QG-P3)
- QA-P10.QG-P2(-2 : 3 = QA-AntiComplement of QG-P2)
- QA-P3.QL-P1

Note: The collinearity of QG-P1, QA-P3 and QL-P1 is discussed at [34], QFG-messages #2987, #2989, #2990, #2992, #3000, #3009, #3011, #3027, #3029 and proven synthetically at [60], page 150 (O ~ QA-P3, R ~ QG-P1, Mr ~ QL-P1).

QG-P1 is the point with minimal sum of distances to the vertices.
QG-P1 is the Railway Watcher (see QL-L-1) of the 1^st and 2^nd QG-Quasi Euler Line QG-L4 and QG-L5 (note Eckart Schmidt).
QG-P1 is the Diagonal Crosspoint of the 2nd Quasi Incenter Quadrigon (explanation “2nd Quasi”, see QG-P8).
QG-P1 is the Isogonal Conjugate of QG-P16 (Schmidt Point) wrt the Miquel Triangle (QA-Tr2). (Eckart Schmidt, November 26, 2012)
The Polar (see [13], Polar) of QG-P1 wrt any inscribed or circumscribed conic of the Reference Quadrigon is the 3^rd diagonal QG-L1.
The Polar (see [13], Polar) of any point on QG-L1 wrt any inscribed or circumscribed conic of the Reference Quadrigon is a line through QG-P1.
The QA-Orthopole (QA-Tf3) of QG-P1 is a point on the Newton Line QL-L1.
The QA-Möbius Conjugate (QA-Tf4) of QG-P1 is a point on the line QA-P4.QG-P18.
The QL-Clawson-Schmidt Conjugate (QL-Tf1) of QG-P1 is QA-P4.
When the Reference Quadrigon P1.P2.P3.P4 is convex, then Area(QG-P1.P1.P2) * Area(QG-P1.P3.P4) = Area(QG-P1.P2.P3) * Area(QG-P1.P4.P1). See [41, pages 27,28].
The circle defined by the 3 versions of QG-P1 (QA-Ci1) in a Quadrangle is incident with QA-P2 and QA-P30.
The Triple Triangle of QG-P1 is perspective with all QA-Component Triangles (see QA-Tr-1 for Desmic Triple Triangles).

Estimated human page views: 623