QG-L2: The Harmonic Line

The Harmonic Line is the line through QA-P16 (the harmonic point of a Quadrangle) and QL-P13 (the harmonic point of a Quadrilateral) both meeting in their overlap of a Quadrigon.

CT-Coefficients QG-L2 in 3 QA-Quadrigons

(q r (-q + r) : p r (2 p + q + r) : -p q (2 p + q + r))

(q r (p + 2 q + r) : p r (r – p) : -p q (p + 2 q + r))

(q r (p + q + 2 r) : -p r (p + q + 2 r) : p q (-p + q))

CT-Coefficients QG-L2 in 3 QL-Quadrigons

( 2 l² (m – n) , m (l m – l n + m n) , -n (-l m + l n + m n) )

( l (l m + l n – m n) , 2 m² (l – n) , -n (-l m + l n + m n) )

( l (l m + l n – m n) , -m (l m – l n + m n) , 2 (l – m) n² )

DT-Coefficients QG-L2 in 3 QA-Quadrigons

( r² : 0 : -p²)

( 0 : -r² : q²)

(-q² : p² : 0 )

DT-Coefficients QG-L2 in 3 QL-Quadrigons

( l² : 0 : -n²)

( 0 : -m² : n²)

(-l² : m² : 0 )

Properties

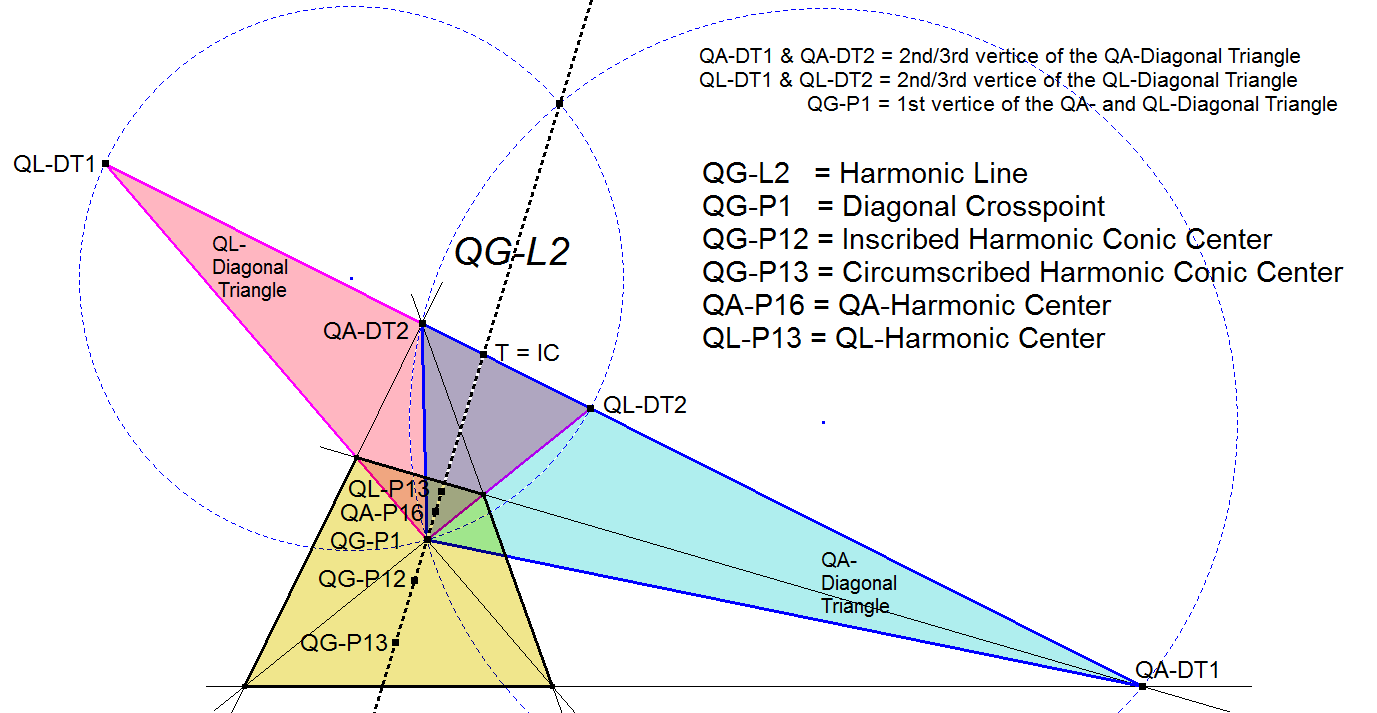
• QA-P16, QL-P13 are collinear with QG-P1, QG-P12 and QG-P13.
• QG-L2 is the radical axis of the circumcircle of the QA-Diagonal Triangle and the circumcircle of the QL-Diagonal Triangle.
• Let T be the intersection point QG-L1^QG-L2.

• Now (QG-P1,T) and (QG-P12,QA-P16) are harmonic conjugated pairs on QG-L2
• also (QG-P1,T) and (QG-P13,QL-P13) are harmonic conjugated pairs on QG-L2.
• T is also the Involution Center of (QL-DT1,QL-DT2) and (QA-DT1,QA-DT2).
• (notes Eckart Schmidt)

• QG-P13, QG-P12, QG-P1, QA-P16, QL-P13 also can be seen as a consecutive perspective row with vanishing point T. See [26b pages 24, 47, 48].
• The 3 variants of QG-L2 in a Quadrangle concur in QA-P16.
• The 3 variants of QG-L2 in a Quadrilateral concur in QL-P13.

Estimated human page views: 463