← Previous Next →

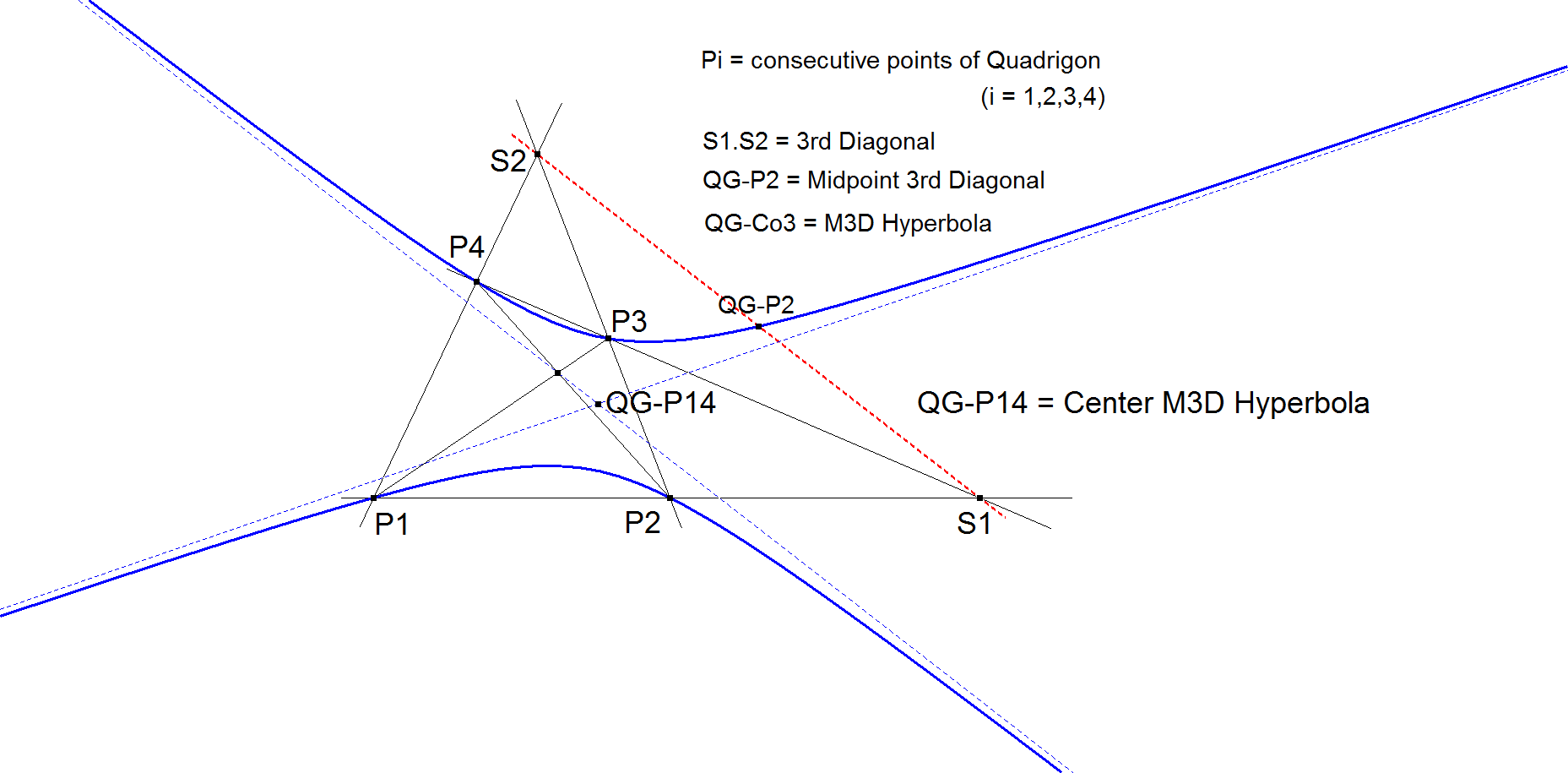
QG-P14 Center of the M3D Hyperbola

QG-P14 is the center of the M3D Hyperbola (see paragraph QG-Co3).

M3D stands for “Midpoint 3rd Diagonal”.

Infovisual QG-P14-infovisual-cvt-01.png
CT-Coordinates QG-P14 in 3 QA-Quadrigons

(p (q + r) (-p q + p r + 3 q r + r2) : q (p – r)2 (p + 2 q + r) : (p + q) r (p2 + 3 p q + p r – q r))

(p (q + r) (p q + q2 – p r + 3 q r) : q (p + r) (p2 + p q + 3 p r -q r) : (p – q)2 r (p + q + 2 r))

(p (q – r)2 (2 p + q + r) : q (p + r) (-p q + 3 p r+- q r + r2) : (p + q) r (3 p q + q2 – p r + q r))

CT-Coordinates QG-P14 in 3 QL-Quadrigons

(-l n (-2 l m2 + l m n + 2 m2 n + l n2 – m n2) : m (l – n) (l2 m – l2 n – 2 l m n – l n2 + m n2) :

l n (-l2 m + 2 l m2 + l2 n + l m n – 2 m2 n))

(l m (l m2 + l m n – m2 n – 2 l n2 + 2 m n2) : -l m (l2 m – l2 n + l m n + 2 l n2 – 2 m n2) :

(l – m) n (l2 m + l m2 – l2 n + 2 l m n – m2 n))

(l (m – n) (l m2 – 2 l m n – m2 n + l n2 – m n2) : -m n (-2 l2 m + 2 l2 n + l m n – l n2 + m n2) :

m n (2 l2 m – l m2 – 2 l2 n + l m n + m2 n))

CT-Area of QG-P14-Triangle in the QA-environment

16 p q r (p2 + p q + p r – q r) (p q + q2 – p r + q r) (p q – p r -q r – r2) Δ

/ ((p + q)3 (p + r)3 (q + r)3)

CT-Area of QG-P14-Triangle in the QL-environment (equals 3 x area QL-Diagonal Triangle)

12 l2 m2 n2 Δ / ((-l m + l n + m n) (l m + l n – m n) (l m – l n + m n))

–

DT-Coordinates QG-P14 in 3 QA-Quadrigons

(-p2+r2 : q2 : p2-r2)

( p2 : -q2+r2 : q2-r2)

(-p2+q2 : p2-q2 : r2)

DT-Coordinates QG-P14 in 3 QL-Quadrigons

(-1 : (l2-n2)/(2 m2) : 1)

((n2-m2)/(2 l2) : 1 : -1)

( 1 : -1 : (m2-l2)/(2 n2))

DT-Area of QG-P14-Triangle in the QA-environment

-(-p2+q2+r2)(p2-q2+r2) (p2+q2-r2) S / (2 p2 q2 r2)

DT-Area of QG-P14-Triangle in the QL-environment (equals 3 x area QL-Diagonal Triangle)

3 S / 2

Properties
  • QG-P14 lies on these lines:
  • QA-P2 (Euler-Poncelet Point) lies on the circumcircle of the triangle formed by the 3 QA-versions of QG-P14.
  • QG-P14 lies on the Nine-point Conic QA-Co1.
  • So the vertices of the triangle formed by the 3 QA-versions of QG-P14 lie on the Nine-point Conic QA-Co1.
  • QG-P14 is the QA-DT-Trilinear Pole of the QL-DT-Trilinear Polar of QG-P13 (Eckart Schmidt, October 13, 2012). For definition Trilinear Pole and Polar see [13].
  • QG-P14 is the 4th point of intersection of the two QA-DT circumscribed conics with centers in the midpoint of the diagonals of the Reference Quadrigon (Eckart Schmidt, November 26, 2012).


Estimated human page views: 529

Scroll naar boven