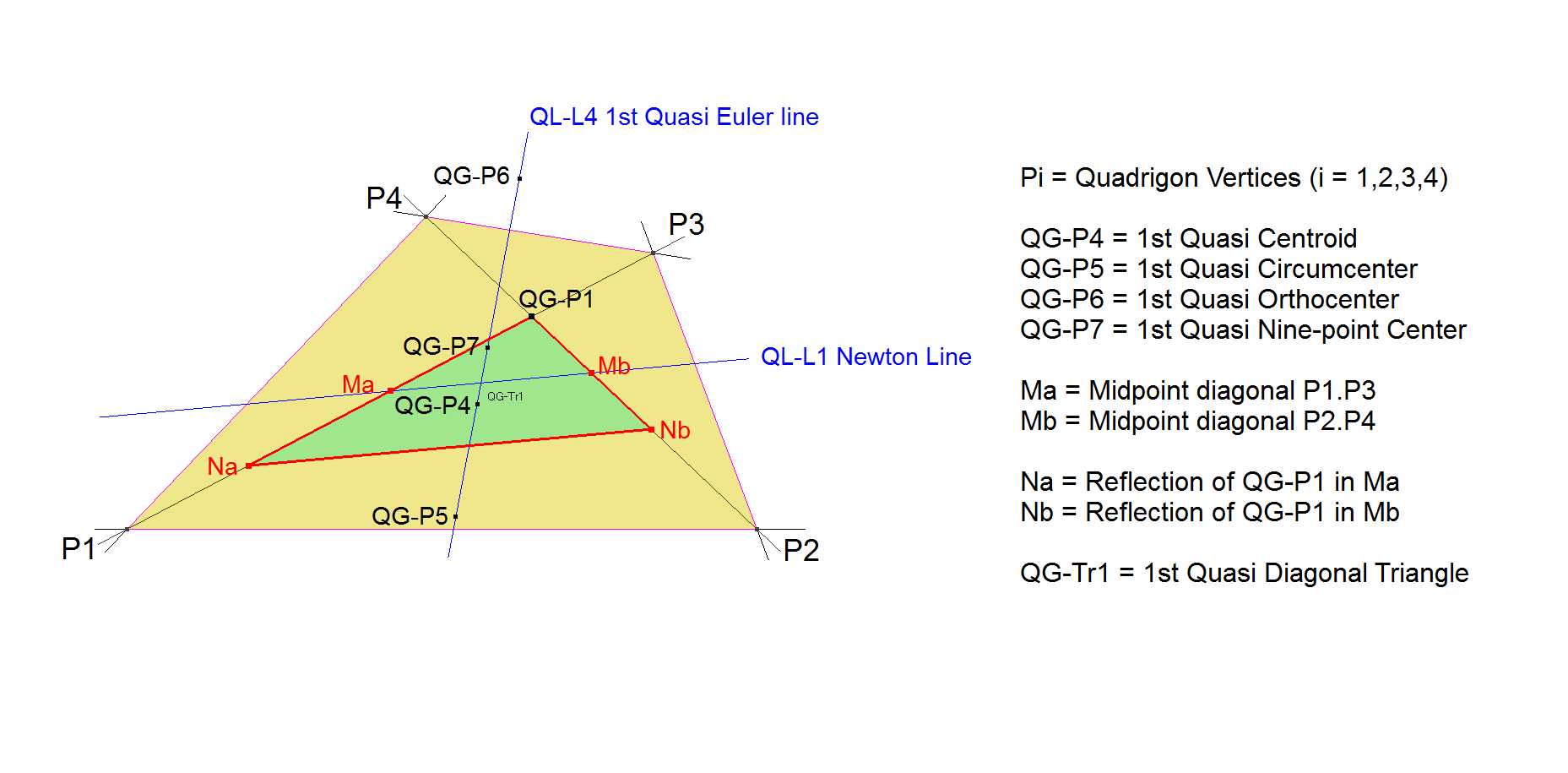
QG-Tr1: 1^st QG-Quasi Diagonal Triangle

QG-Tr1 is the Triangle with vertices QG-P1 (Diagonal Crosspoint) and the Reflections of QG-P1 in the 2 Diagonal Midpoints of the Reference Quadrigon.

Special about this triangle is that the 1^st Quasi points QG-P4, QG-P5, QG-P6, QG-P7 are the corresponding triangle points of this Triangle.

For example the 1^st Quasi Centroid QG-P4 of the Reference Quadrigon is also the Triangle Centroid of QG-Tr1.

This means that the Centroid of a Quadrigon also can be constructed as the Centroid of the 1^st QG-Quasi Diagonal Triangle.

Area QG-1^st Diagonal Triangle in 3 QA-Quadrigons CT-notation

(r – p) (p + 2 q + r) S / (2 (r + p) (p + q + r))

(q – r) (2 p + q + r) S / (2 (q + r) (p + q + r))

(p – q) (p + q + 2 r) S / (2 (p + q) (p + q + r))

Area QG-1^st Diagonal Triangle in 3 QL-Quadrigons CT-notation

(-l m + l n + m n) (l m + l n – m n) S / (2 (m – l) (m – n) ( l m – l n + m n))

( l m – l n + m n) (l m + l n – m n) S / (2 (n – l) (n – m) (-l m + l n + m n))

(-l m + l n + m n) (l m – l n + m n) S / (2 (l – m) ( l – n) ( l m + l n – m n))

–

Area QG-1^st Diagonal Triangle in 3 QA-Quadrigons DT-notation

4 p r (p – r) (p + r) S / ((p + q + r) (-p + q + r) (p + q – r) (p – q + r))

4 q r (q – r) (q + r) S / ((p + q + r) (-p + q + r) (p + q – r) (p – q + r))

4 p q (q – p) (q + p) S / ((p + q + r) (-p + q + r) (p + q – r) (p – q + r))

Area QG-1^st Diagonal Triangle in 3 QL-Quadrigons DT-notation

2 m⁴ S / ((m² – l²) (m² – n²))

2 n⁴ S / ((n² – l²) (n² – m²))

2 l⁴ S / ((l² – m²) (l² – n²))

Properties

• The 1st QG-Quasi Euler line QG-L4 is also the Triangle Euler line of QG-Tr1.
• The points 1^st Quasi Centroid/Circumcenter/Orthocenter/Nine-point Center (resp. QG-P4, QG-P5, QG-P6, QG-P7) are also the Centroid/Circumcenter/ Orthocenter/Nine-point Center of QG-Tr1.

Estimated human page views: 466