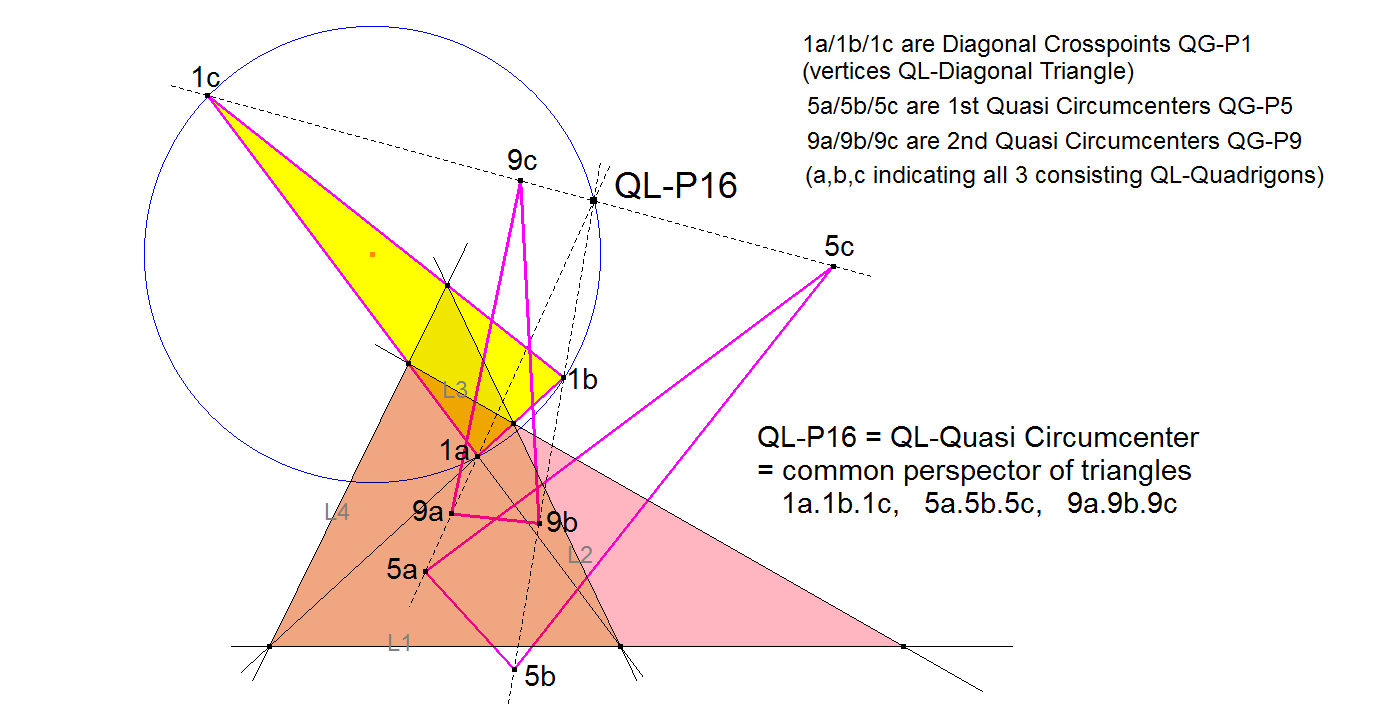
QL-P16: QL-Quasi Circumcenter

QL-P16 is the perspector of the QL-Diagonal Triangle and the Triangle formed by the points QG-P5 (QG-1^st Quasi Circumcenter) of the 3 QL-Quadrigons.

QL-P16 is also the perspector of the QL-Diagonal Triangle and the Triangle formed by the points QG-P9 (QG-2^nd Quasi Circumcenter) of the 3 QL-Quadrigons.

1^st CT-coordinate

m n (32 a² Δ² (l – m) (l – n) (l m – l n + m n) (-l m + l n + m n) (-m n + l m + l n)

– (a² m n (l – m) (l – n) + b² l n (m – l) (m – n) + c² l m (n – l) (n – m))

* (4 a⁴ l² (l m + l n – m n) – a⁴ (l m + l n – m n)² – b⁴ (l m – l n + m n)² – c⁴ (-l m + l n + m n)²

+ 2 b² c² (l² m² – 2 l² m n + l² n² + m² n²)

+ 2 a² b² (2 l³ m – 3 l² m² – 2 l³ n + 2 l² m n + l² n² – 2 l m n² + m² n²)

+ 2 a² c² (-2 l³ m + l² m² + 2 l³ n + 2 l² m n – 2 l m² n – 3 l² n² + m² n²)))

1^st DT-coordinate

a² (Sc l² – b² m² + Sa n²) (Sb l² + Sa m² – c² n²)

Properties

• QL-P16 lies on this line:
  • QL-P1.QL-P10                  (-1 : 2 => QL-P16 = Reflection of QL-P10 in QL-P1)
• QL-P16.QL-P9 // QL-P1.QL-P11.
• QL-P16 lies on the circumcircle of QL-Ci1, the QL-Diagonal Triangle.
• QL-P16 lies on the circumcircles of triangles formed by the 3 QL-versions of QG-P1, QG-P5 as well as QG-P9.
• QL-P16 is Railway Watcher (see QL-L-1) of lines QL-L5 (NSM Line) and QL-L6 (Quasi Ortholine).

Estimated human page views: 450