← Previous Next →

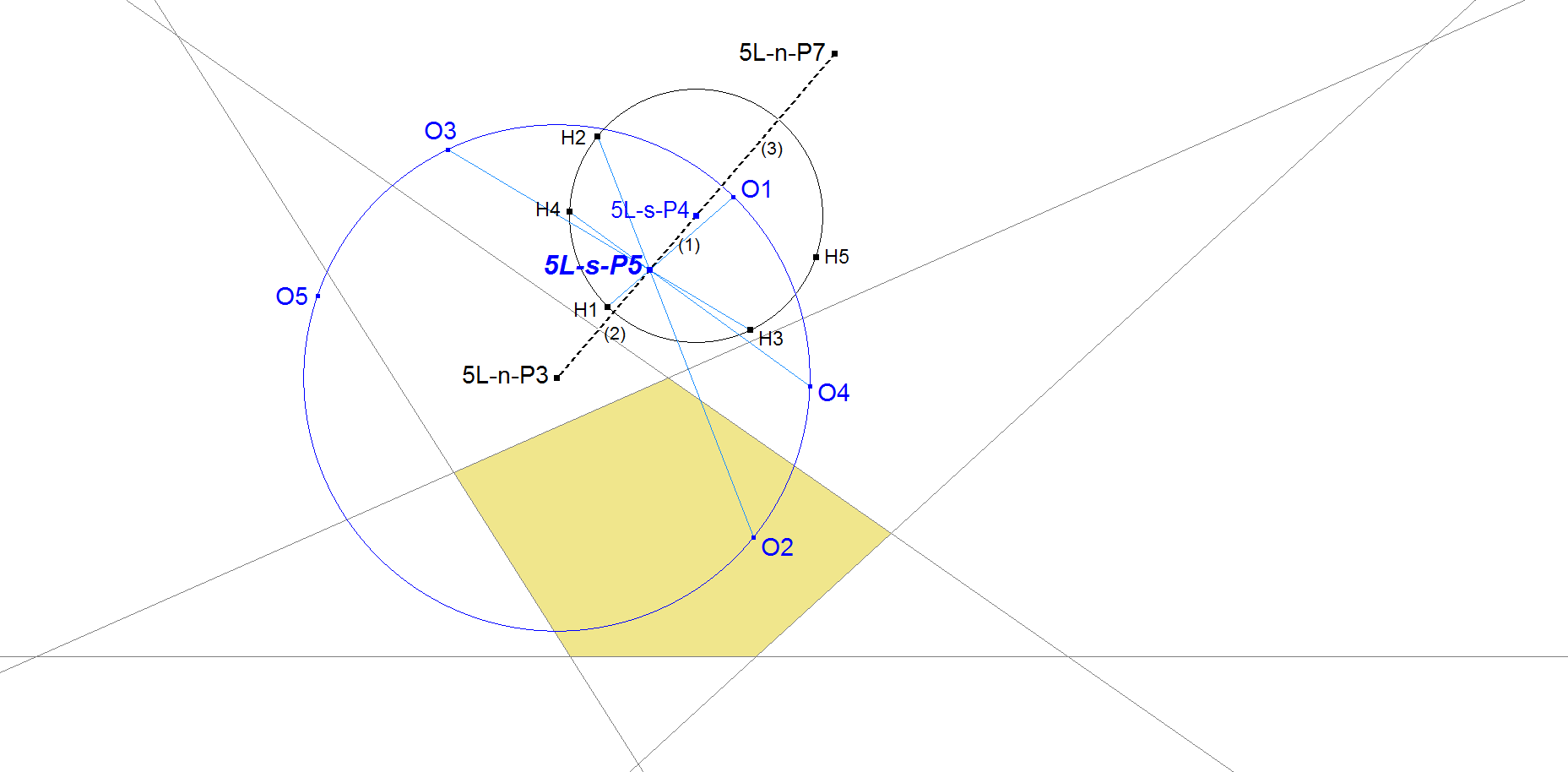
5L-s-P5: 5L-OH Division Point

Let Oi (i=1,2,3,4,5) be the concyclic 4L-Circumcenters (4L-n-P3).

Let Hi be the anticenter of Oj.Ok.Ol.Om, where (i,j,k,l,m) are different numbers from (1,2,3,4,5).

H1, H2, H3, H4, H5 are concyclic on a circle with center 5L-s-P4.

The lines Hi.Oi (i=1,2,3,4,5) have a common point 5L-s-P5.

5L-s-P5 divides 5L-n-P3.5L-n-P7 as well as Hi.Oi (i=1,2,3,4,5) in parts (1:2).

There is a remarkable resemblance in a 4-Line where QL-P5 is dividing Hi.Oi (1:1).

See also [34], QFG#1904.

Infovisual 5L-s-P5-infovisual-cvt-01.png
Properties
  • 5L-s-P5 is the Ratiopoint 5L-n-P3.5L-n-P7(2:1).
  • Radius O-circle = 2 * Radius H-circle.
  • The distribution of H-Points on the H-circle is similar to the distribution of O-points on the O-circle. They represent the angles between the defining lines of the 5-Line. See [34], QFG#1893.


Estimated human page views: 262

Scroll naar boven