nL-n-P3: nL-Morley’s Circumcenter / Centric Center

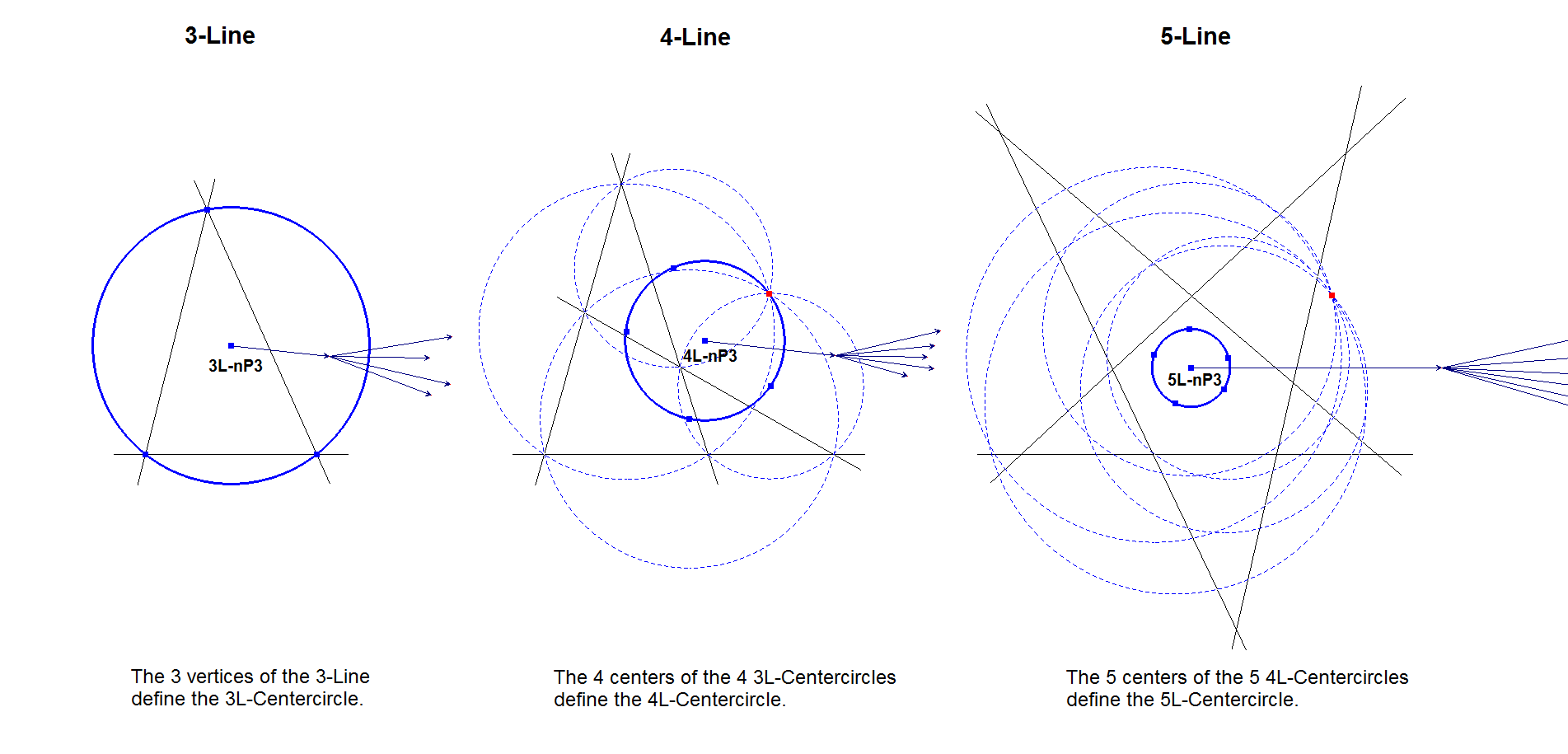
A Triangle (3-Line) has a circumcircle. Morley in Ref-49 calls this circle a Centercircle.

In a Quadrilateral (4-Line) there are 4 component 3-Lines whose 3L-Centercircle Centers are concyclic on the 4L-Centercircle.

In a Pentalateral (5-Line) there are 5 component 4-Lines whose 4L-Centercircle Centers are concyclic on the 5L-Centercircle. Etc.

Morley proved in Ref-49 that there exists a Centercircle in an n-Line for all n, built from the centers of the Centercircles from the Component m-Lines.

The Center of this Centercircle is shortly named the Centric Center by Goormaghtigh in Ref-55.

This nL-Centric Center is the basis for several other Morley points.

Morley uses the letter “a₁“ or “p₀“ for this point in Ref-49.

Morley describes in Ref-49 some recursive points “p_i“ for i=1, .. , n/2 (see nL-n-pi) that are useful for constructing some other points. In this notation nL-n-P3 = p₀ (or in EPG notation: nL-n-p0).

Correspondence with ETC/EQF

• When n=3, then nL-n-P3 = X(3).
• When n=4, then nL-n-P3 = QL-P4.

Properties

• 5L-n-P3 is the ratiopoint 5L-s-P4.5L-s-P5 (3:-2).

Estimated human page views: 271