CU-8P-P1 Cayley-Bacharach point

Cayley-Bacharach’s theorem states that when P1,P2,P3,P4,P5,P6,P7,P8 are points on a cubic, that all other cubics passing through these 8 points will have a common 9th point.

The 9th point is then the Cayley Bacharach Point of the other 8 points.

Define CB9 = Cayley-Bacharach Point of P1, …, P8.

We know from the CU Point Addition Method (CU-4) that P1+P2+P3+P4+P5+P6+P7+P8+CB9=3N.

Therefore CB9=3N-PP8.

Knowing this formula of the Cayley-Bacharach Point we can deduct this construction method CB9=(P1.P2).(P3.P4).(P5.P6).(P7.P8), where the . operation Pi.Pj means “construct 3rd intersection point of Cu and line PiPj”.

It is easy to calculate that CB9=3N-PP8 following this construction and using rule 6. It is also clear that any point of the set of 8 points can be taken as P1, etc. So the construction can be done in multiple ways delivering the same point CB9.

Moreover it proves in a simple way the existence of the Cayley-Bacharach point.

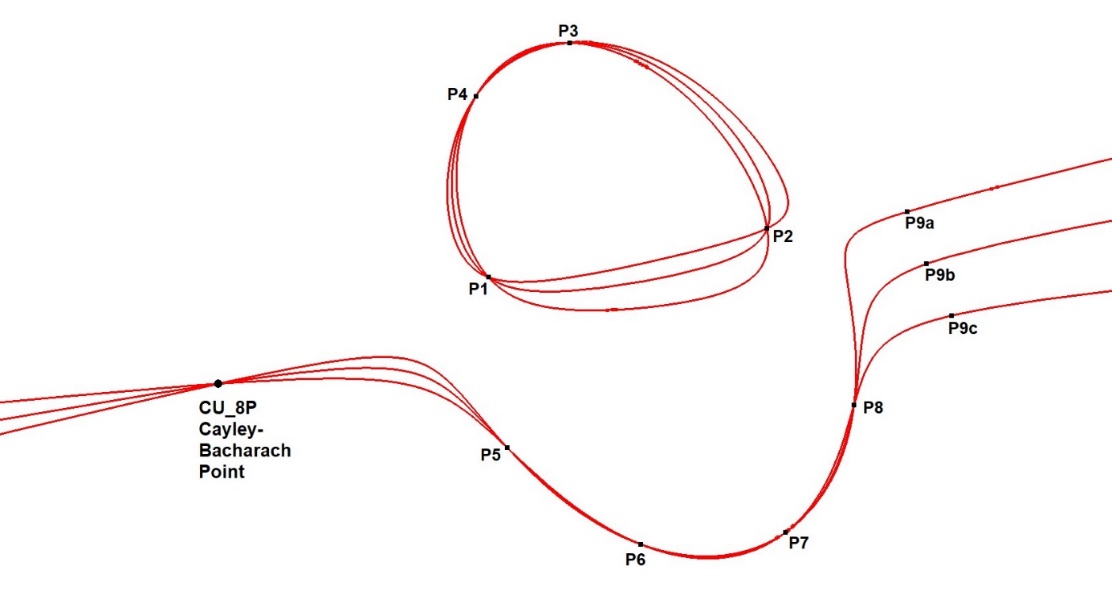
CU-8P-P1 CU-8P Cayley-Bacharach Point-01.fig

CU Point Validation

• P1+P2+P3+P4+P5+P6+P7+P8 + CU-8P-P1 = 3N
• Therefore CU-8P-P1 = 3N – PP8.

Another construction

From the CU Point Validation, a construction for the Cayley-Bacharach Point emerges by successively intersecting connection lines among the eight reference points as follows: for each pair of points, a third CU-point is determined; these CU-points are then paired and connected again to yield new CU-points. This hierarchical process continues until the final intersection of the last two CU-points produces a point that coincides with the Cayley-Bacharach Point.

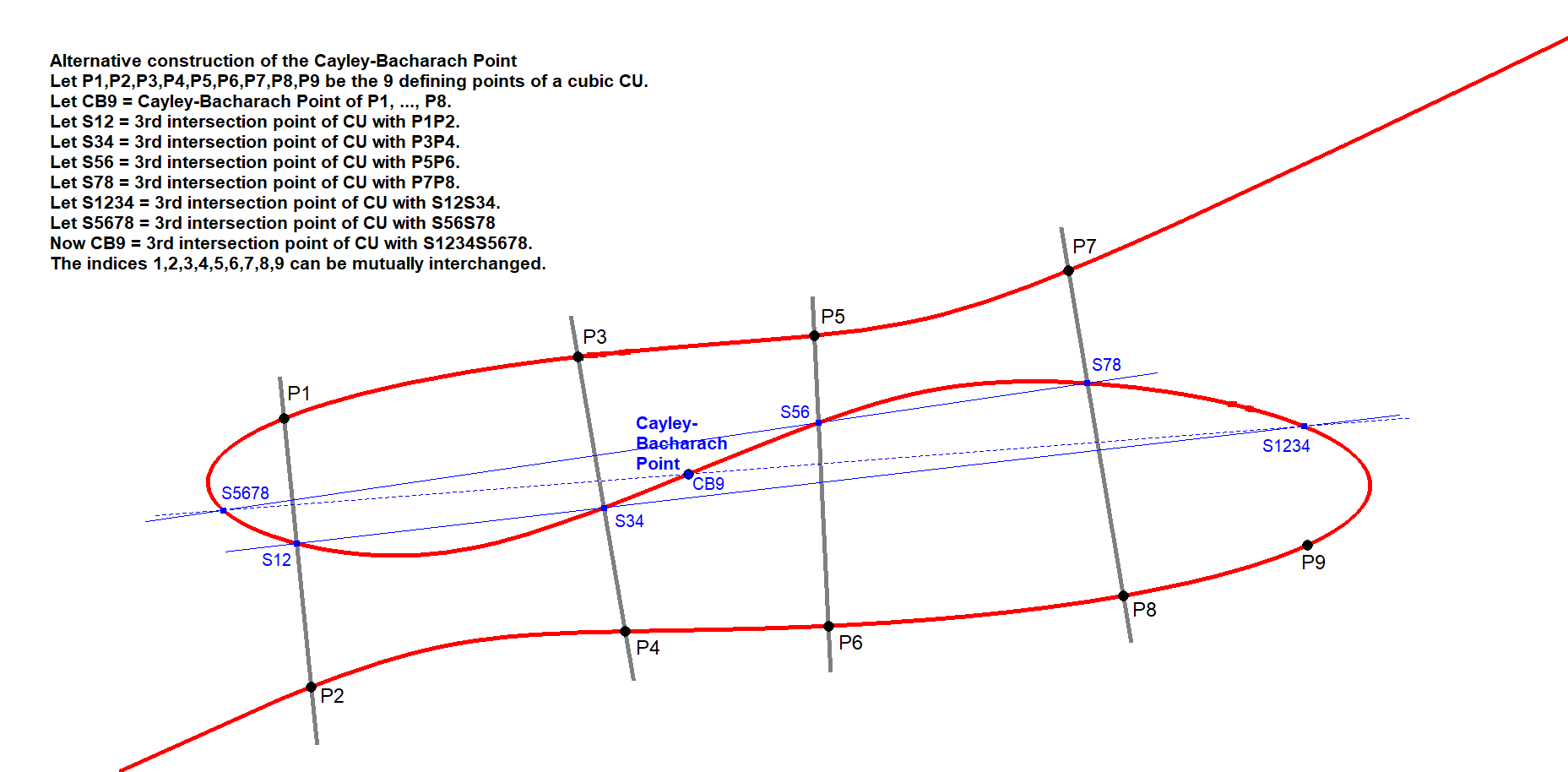
8P-s-P1” target=”_blank”>8P-s-P1-Cayley-Bacharach Point-11-Alternative-Construction.png

Estimated human page views: 8