CU-P-Tf1 P-Involutary Conjugate

On a general cubic we have 4 points of tangency (CU-P-4P1) of tangents from some point P to the cubic. They are the intersection points of CU and the P-Polar Conic (CU-P-Co1).

These 4 points form a Quadrangle QA. For each such QA exists an Involutary Conjugate (see QA-Tf2 in EQF) mapping any point on CU to another point on CU.

It is a P-pivotal transformation because all points to be mapped and mapped points are lined up with (pivot-)point P.

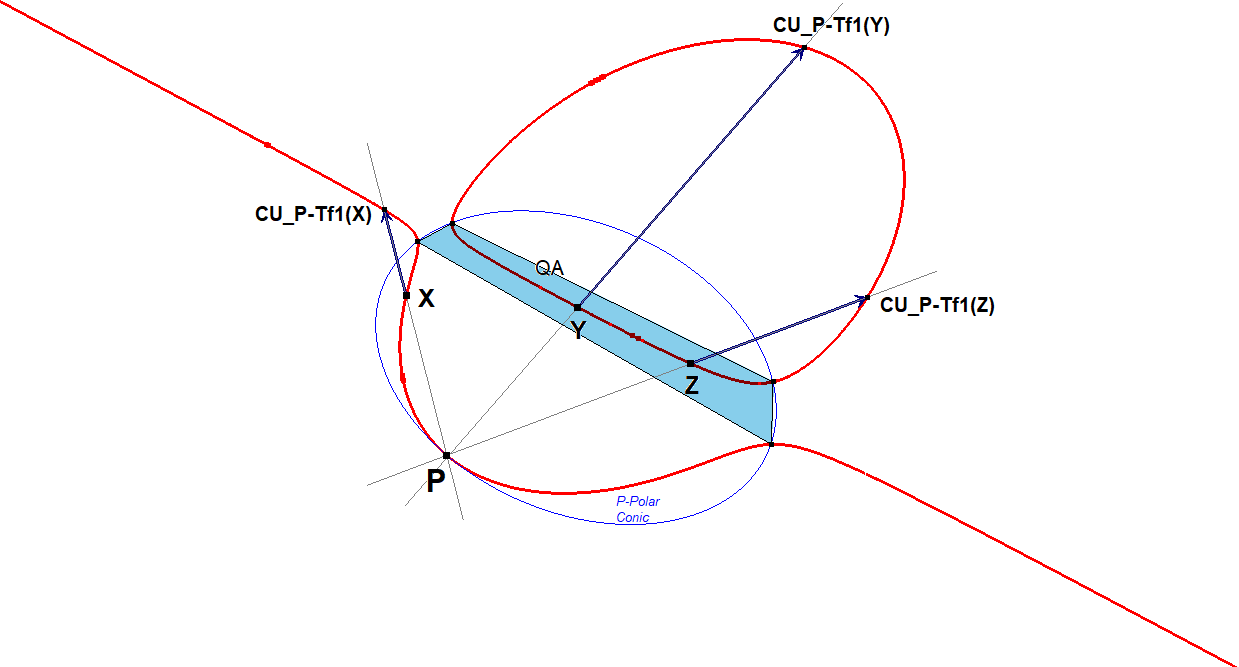
CU-P-Tf1 P-pivotal QA-Tf2-00.fig

An isocubic is defined as a circumcubic wrt some reference triangle which is invariant under an isoconjugation. The Diagonal Triangle QA-DT of the defined QA above has its points on CU and therefore CU is a circumcubic of QA-DT and can function as reference triangle. The vertices of QA are the 4 fixed points of QA-Tf2, meaning that these points are transformed to itself by QA-Tf2.

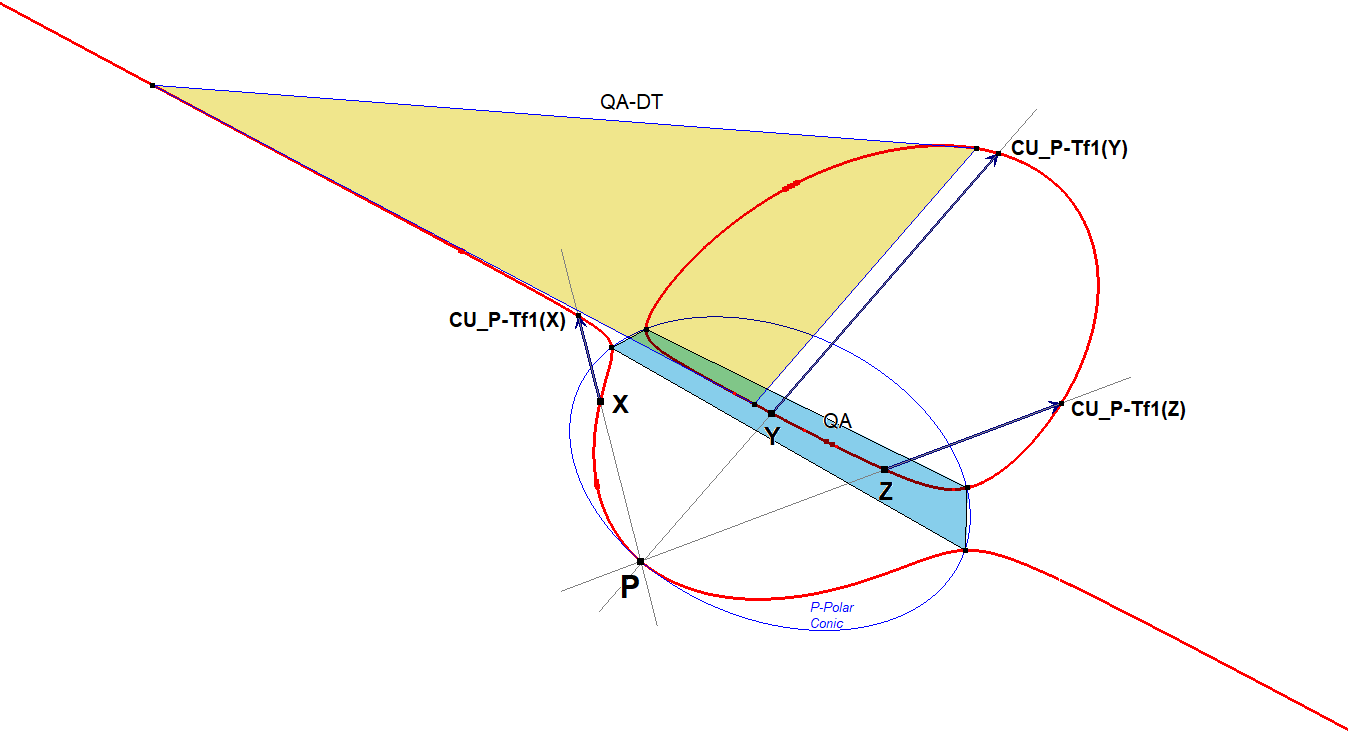
CU-P-Tf1 P-pivotal QA-Tf2-01.fig

It is said that QA-Tf2 is an isoconjugation and therefore any general cubic with some point P having 4 real points of tangency (CU-P-4P1) on the cubic will be an isocubic.

Two constructions

Eckart Schmidt makes note of two other triangular constructions wrt the QA-DT at QPG#2035 and QPG#2068 that bring about the same transformation as QA-Tf2.

Here is a summary of these two constructions:

QPG#2035, December 14, 2023

There is this an isoconjugation (reference is a private correspondence of Roland Stärk, 22.11.2002):

An isoconjugation X –> X* wrt a triangle ABC

… can be defined by a circumscribed conic CO,

… starting with a point X, take the intersection A’ = XA ^ CO

… and consider the intersection Xa of CO

… and a parallel to BC through A’,

… analog we get Xb and Xc with the image X* = AXa ^ BXb ^CXc.

Examples of isoconjugations for a triangle:

… isogonal for CO = circumcircle,

… isotomic for CO = Steiner circumellipse,

… QA-Tf2 for a QA: CO = QA-Co1,

… in general for an isoconjugation: CO = image of the line at infinity.

QPG#2068, January 7, 2024

An isoconjugation X–>X* can be defined

… for a triangle ABC and a fixed point K.

Let Ka = AK^BC, Xa = AX^BC,

… Ka’ = 4th harmonic of Ka wrt BC,

… Xa’ = 4th harmonic of Xa wrt KaKa’,

… X* = AXa’^BXb’^CXc’.

I got this simple construction

… from Günther Pickert 20 years ago.

Estimated human page views: 6