CU-IP-L1 Asymptotes of the Cubic

The 3 asymptotes of a general cubic are CU-IP-L1a, CU-IP-L1b, CU-IP-L1c.

The points at infinity (IP1,IP2,IP3) of the reference cubic are also the points at infinity of the asymptotes.

The asymptote triangle and its vertices are described at CU-IP-Q1.

For a real Cubic there is at least one real asymptote. Two of them can be imaginary.

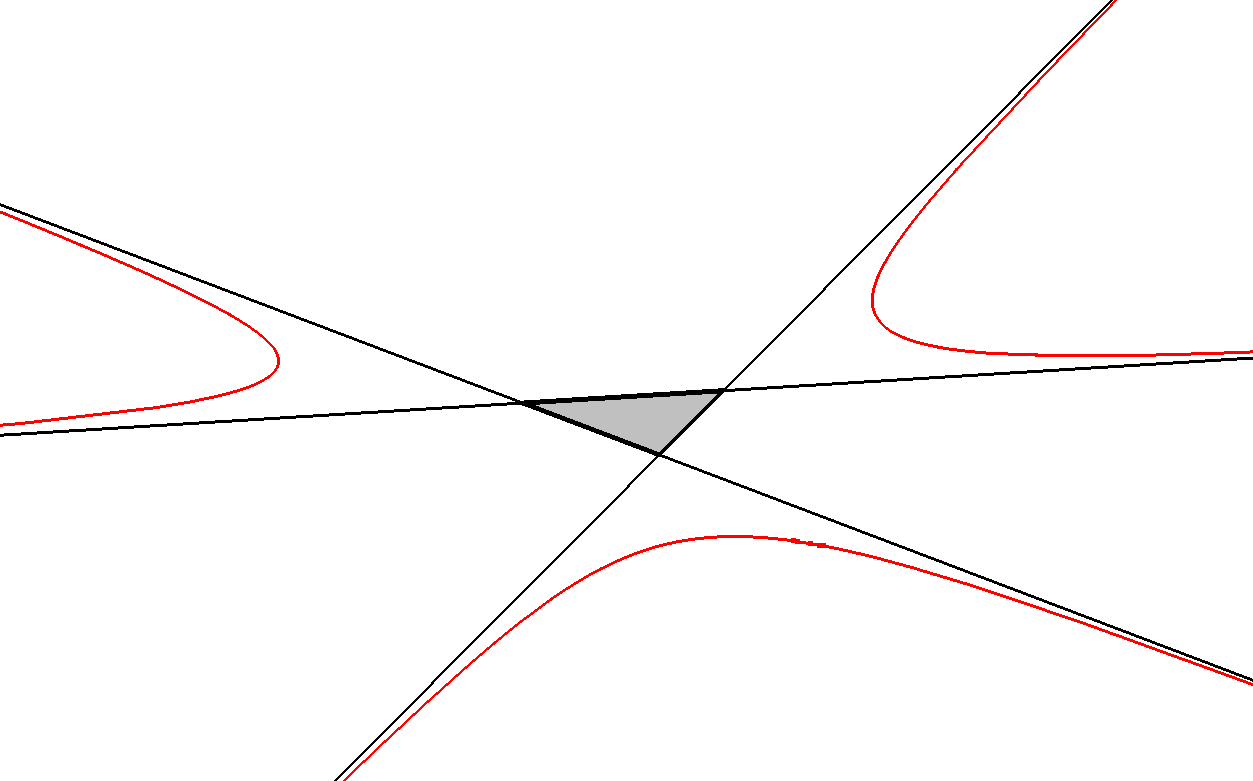
CU-IP-L1 CU-Asy-Triangle-01.fig

Construction

A construction of all 3 asymptotes given 9 points of the cubic can be found at [Cuppens, pages 212,242,243].

Construction of the 2^nd and 3^rd CU-asymptote

When one asymptote is already known, then the 2^nd and 3^rd asymptote can be constructed as follows.

Let IP1 be the infinity point of the known asymptote.

Note that the IP1-Central Conic (CU-IP-Co2) has infinity points IP2 and IP3 on it.

Therefore when IP1, IP2, IP3 are real points and the IP1-asymptote is known, then the IP2- and IP3-asymptotes con be constructed as follows:

• Construct the IP1-Central Conic Co1 as described at CU-IP-Co2.
• Construct its CO1-asymptotes. They will be parallel to the CU-asymptotes with infinity points IP2 and IP3.
• Construct the CU-asymptotes Asy-2 and Asy-3 using the general construction method described at CU-IP-P2.

Properties

• If the cubic has three real asymptotes, then the Lemoine point aka Symmedian Point (X(6) in ETC) of the triangle formed by the asymptotes has a special function. The polar conic of this point wrt the cubic is a circle. See CU-Ci1 and Gibert, Isocubics, [17b], page 21.

Estimated human page views: 6