CU-IP-Q1 Vertices CU-Asymptotes Triangle or Asy-Asy-Crosspoints

The 3 asymptotes of a general cubic form a triangle with vertices CU-IP-Q1a, CU-IP-Q1a, CU-IP-Q1a. When there is only one real version then the only version is called F. Each version is a point diametral to Q (CU-IP-P2) on the corresponding version of a QF-conic (CU-IP-Co2), which also contains the vertices of a Quasi-Miquel Triangle (CU-IP-3P1).

The Polar Conic of a Vertex of the Asy-Triangle contains the same infinity points as the two asymptotes through this vertex and the same infinity points as the corresponding Central Conic/QF-Conic.

There are more properties. See QPG#2045.

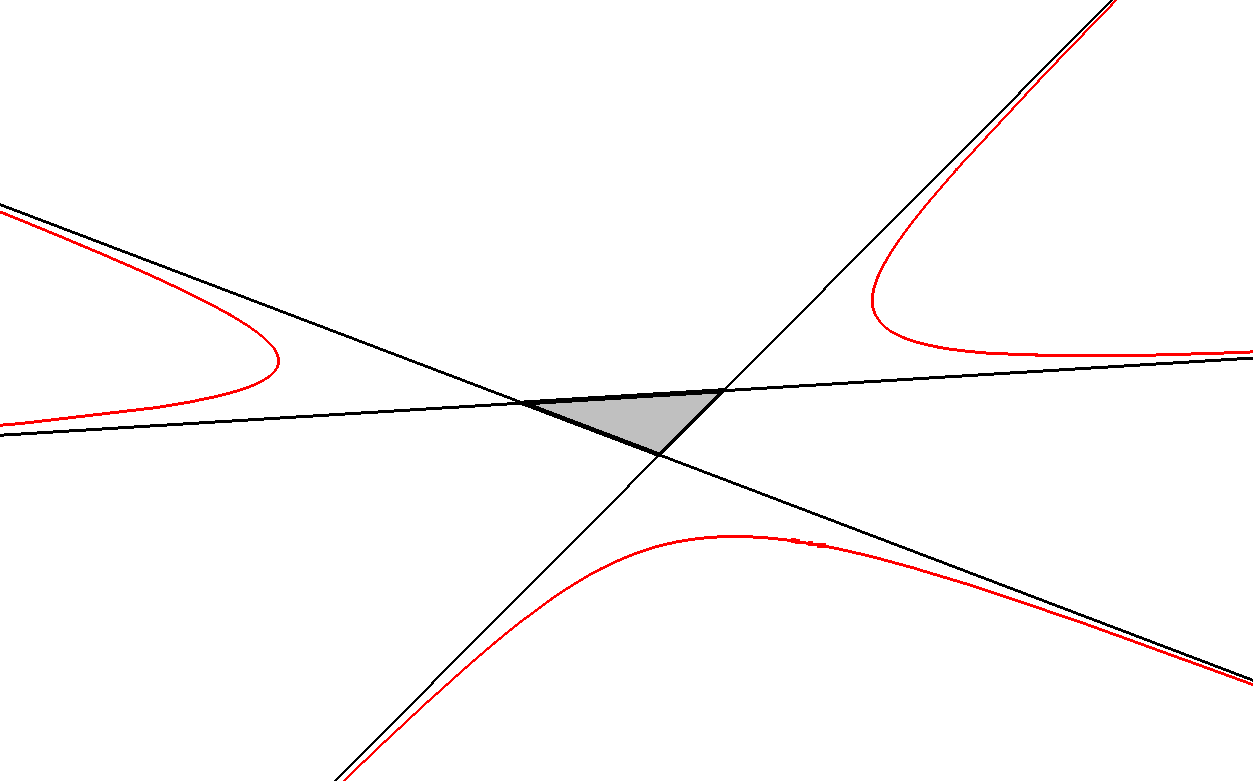
CU-IP-Q1 CU-Asy-Triangle-01.fig

Occurrences for different types of CU

• A real general cubic has three asymptotes. Either one or all three of them are real.
• These asymptotes intersect pairwise at three points (CU-IP-Q1), which may also be either one or three real points.
• One real intersection point can be considered the counterpart of the singular focus found in a circular cubic.
• In some cases, two of the asymptotes may be imaginary lines that intersect at a real vertex, denoted CU-IP-Q1a.

Relationship with CUc (Circular Cubic)

On a circular cubic there is only one real asymptote and only one real vertex F. This single vertex is the real intersection point of the two imaginary asymptotes of the circular cubic and called (the singular) focus of the circular cubic. It is also the common intersection point of the Perpendicular Bisectors of the remaining intersection points of CU and all lines though Q (CU-IP-P2).

Estimated human page views: 4