Translation into English

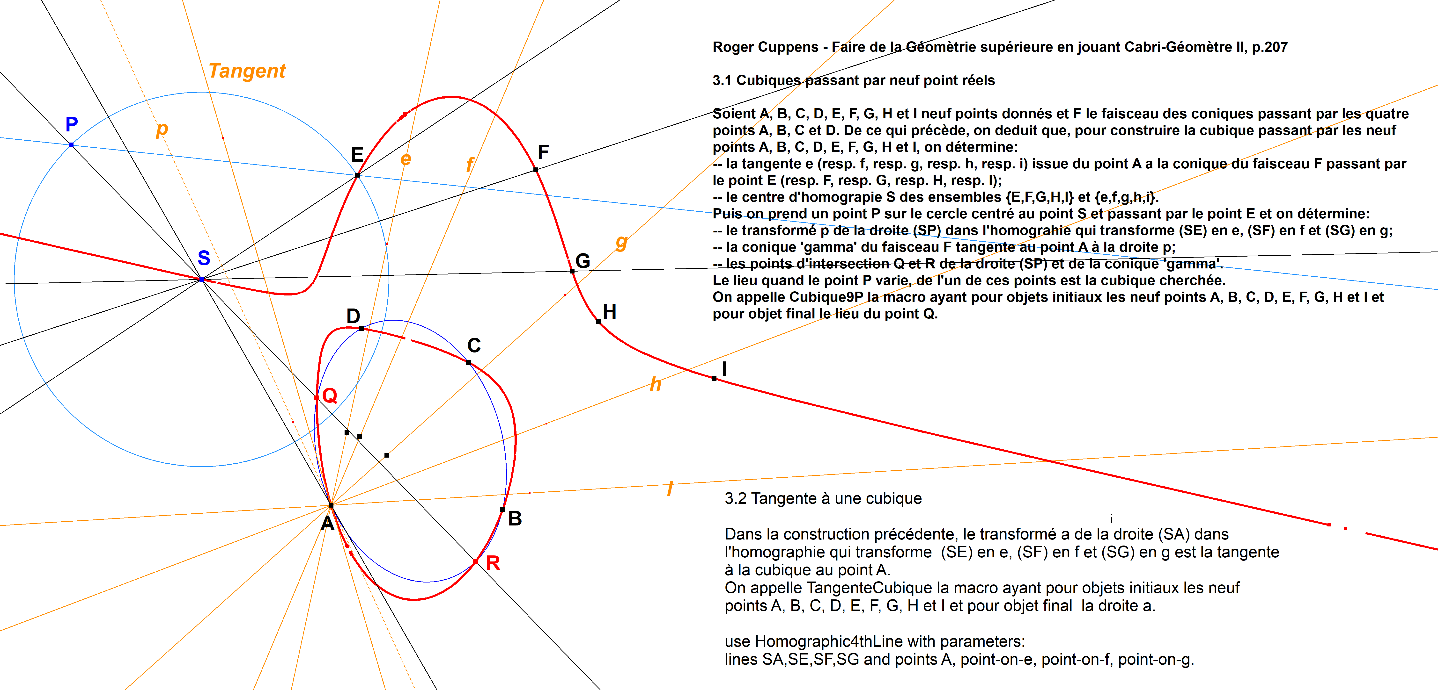
3.1. Cubics passing through nine real points

Let A,B,C,D,E,F,G,H,I be nine given points, and let F be the pencil of conics passing through the four points A,B,C,D. From the preceding, we deduce that to construct the cubic curve passing through the nine points A,B,C,D,E,F,G,H,I, one determines:

the tangent ee (respectively f,g,h,i) from point AA to the conic in the pencil F passing through point E (respectively F,G,H,I);

the center of homography S between the sets {E,F,G,H,I} and {e,f,g,h,i}.

Then, one selects a point PP on the circle centered at S and passing through point E, and determines:

the image p of the line (SP) under the homography that maps (SE) to e, (SF) to f, and (SG) to g;

the conic γ from the pencil F that is tangent at point A to the line p;

the points of intersection Q and R between the line (SP) and the conic γ.

The locus of one of these points, as P varies, is the desired cubic.

This construction is referred to as Cubique9P, a macro whose initial objects are the nine points A,B,C,D,E,F,G,H,I, and whose final object is the locus of point Q.

3.2. Tangent to a Cubic

In the previous construction, the image aa of the line (SA) under the homography that maps (SE) to e, (SF) to f, and (SG) to g, is the tangent to the cubic curve Γ at point A.

The macro TangenteCubique is defined with the nine points A,B,C,D,E,F,G,H,I as its initial objects, and the line a as its final object.