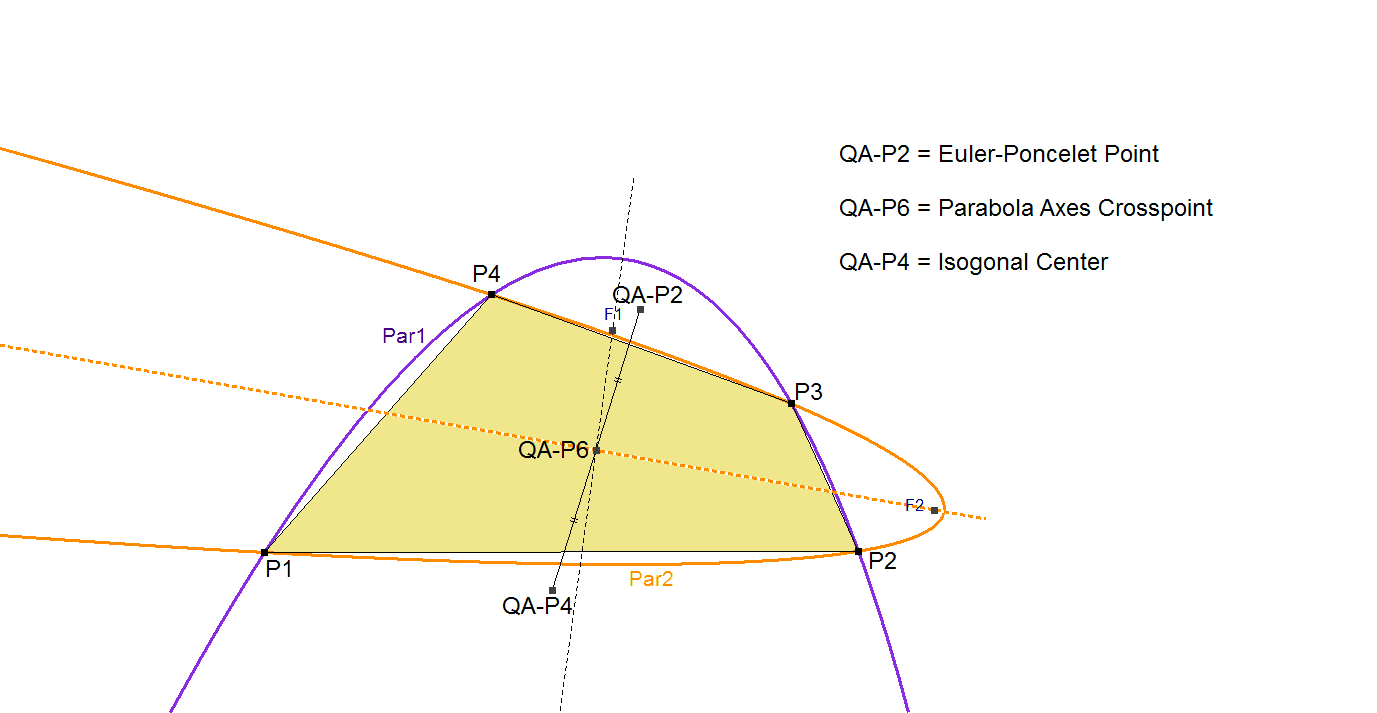
QA-P6:  Parabola Axes Crosspoint

The Parabola Axes Crosspoint is the intersection point of the axes of the 2 parabolas that can be constructed through P1, P2, P3, P4.  It is also is the Midpoint of the Euler-Poncelet Point QA-P2 and the Isogonal Center QA-P4.
Because these parabolas only can be constructed when the Reference Quadrangle is not concave a better definition of this point is: “the Midpoint of the Euler-Poncelet Point and the Isogonal Center”.
Because the property related to the parabolas is much more appealing this point after its primary function.
It also can be reasoned that in a concave quadrangle this point represents the intersection point of the axes of the imaginary parabolas.

1st CT-Coordinate:

a⁴ q² r² + c² p² q² S_B + b² p² r² S_C  –  p q r (a² (p + q + r) S_A + 2 (p S² – q S_B² – r S_C²))

1st DT-Coordinate:

p² (b² S_B  r² + c² S_C q² – c² b² p²)

Properties:

• QA-P6 lies on these QA-lines:
  • QA-P1.QA-P23
  • QA-P2.QA-P4 ( 1 : 1 => QA-P6 = Midpoint QA-P2.QA-P4)
  • QA-P28.QA-P29 (-1 : 2 => QA-P6 = Reflection of QA-P29 in QA-P28)
• QA-P6 is the Involutary Conjugate (see QA-Tf2) of QA-P30.
• QA-P6 lies on the Simson Line (QA-P6.QA-P36) of  QA-P2 occurring on the circumcircle of the QA-Diagonal Triangle.
• QA-P6 is the common point of the 4 Simson Lines of QA-P2 wrt the medial triangles of the component triangles (see [34], QFG#548-550).
• For all QA-Quadrigons QA-P6 is the center of the Pedal Quadrangle of QA-P4 (Isogonal Center) , which is a parallelogram. See [15 f] theorem (23).
• The QA-Orthopole (QA-Tf3) of QA-P6 is the Midpoint(QA-P2,QA-P23).

Estimated human page views: 916