QA-Tf3: QA-Orthopole Transformation
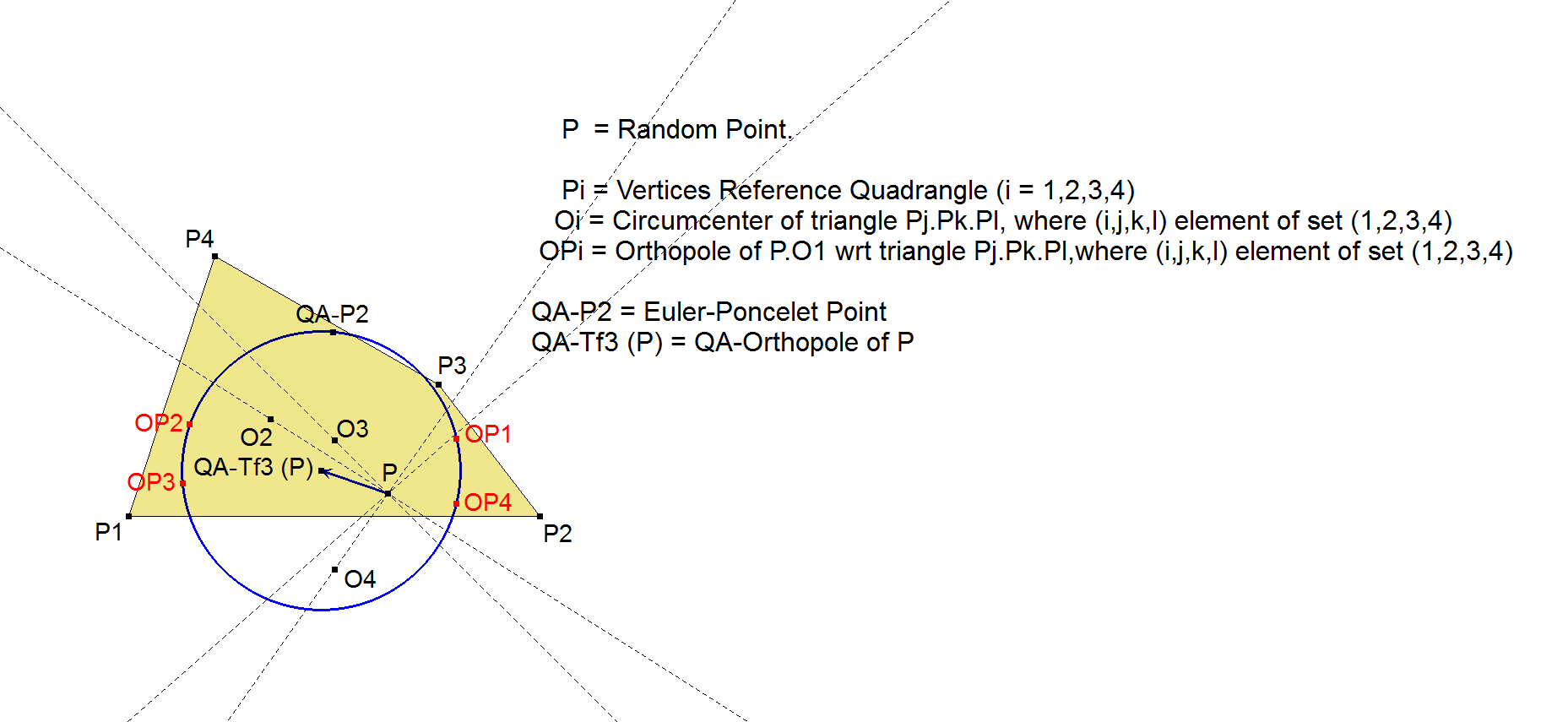
Let P be a random point.
Let O1, O2, O3, O4 be the circumcenters of the Component Triangles of Reference Quadrangle P1.P2.P3.P4.
Let OPi be the Orthopole of line P.Oi wrt Component Triangle Pj.Pk.Pl, where (i,j,k,l) ∈ (1,2,3,4). The 4 Orthopoles OP1, OP2, OP3, OP4 are concyclic.
For an explanation of Orthopole see [13].
The circle through OP1, OP2, OP3, OP4 passes through QA-P2. This construction was found by Antreas P. Hatzipolakis. See [11], Hyacinthos messages # 21865 & 21867.
QA-Tf3 is the Center of the circle through OP1, OP2, OP3, OP4.
The coordinates of the transformed point show that QA-Tf3 is a linear transformation.
When P = QA-P3 then the QA-Orthopole-circle = circle with diameter QA-P2.QA-P3.When P = QA-P4 then the QA-Orthopole-circle = point QA-P2.When P = QA-P12 then the QA-Orthopole-circle = circumcircle of the Diagonal Triangle.
There is another construction for QA-Tf3:
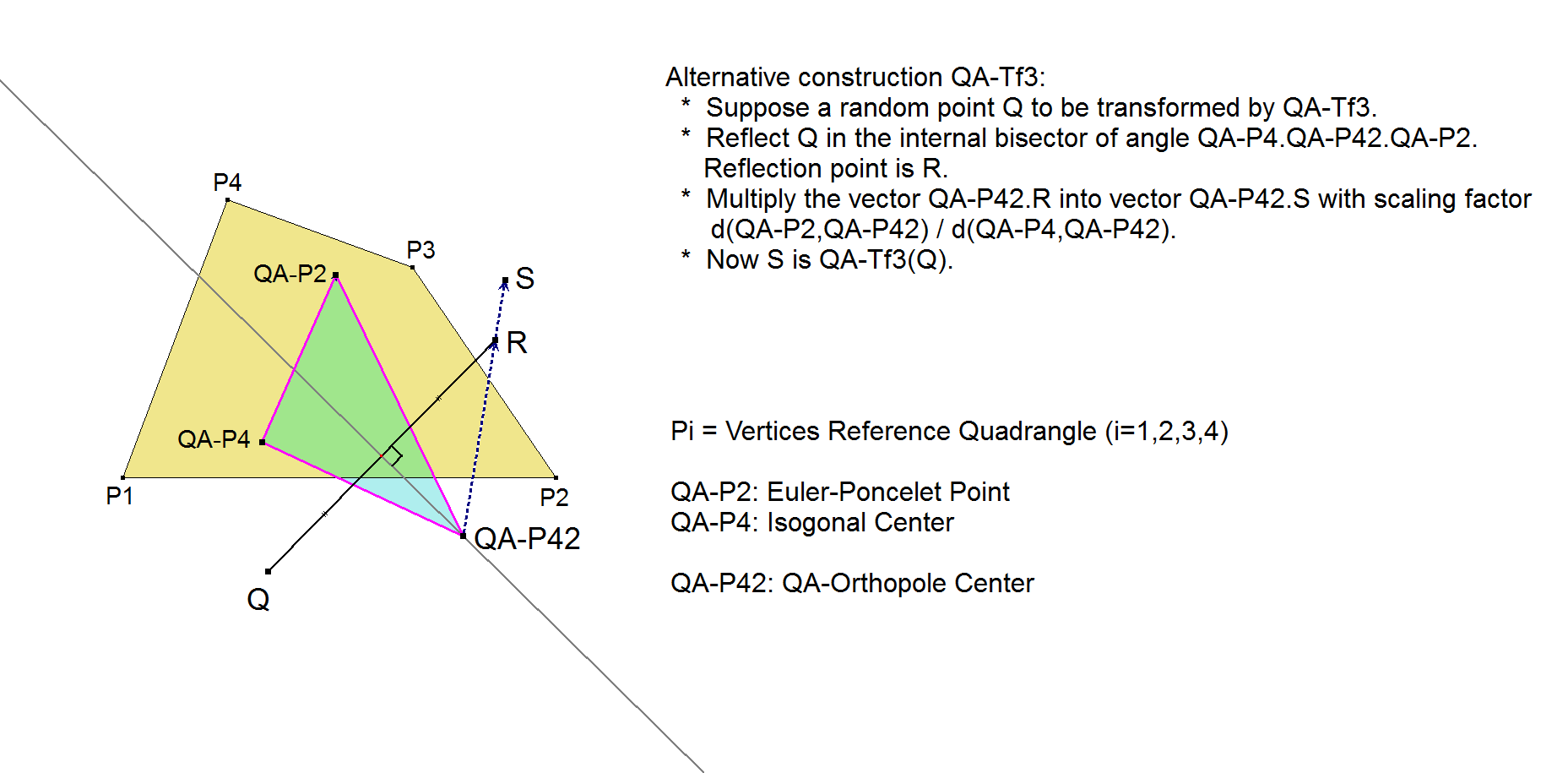
And here is a special property of QA-Tf3:
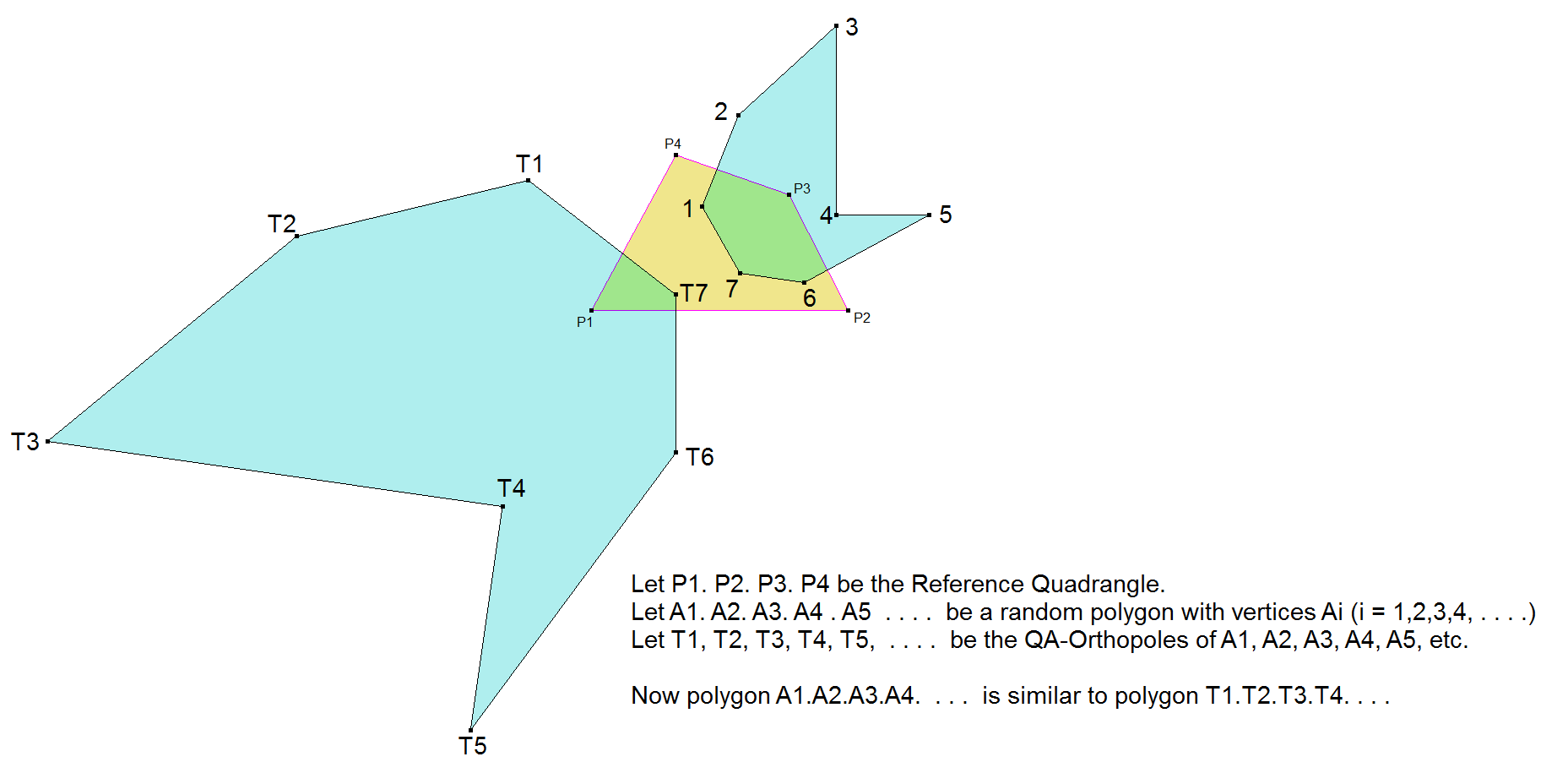
This transformation was earlier described by Benedetto Scimemi (called ‘p’) as a negative similarity transforming the Reference Quadrangle into the Quadrangle of the pedal centers. He refers to H.V. Mallison [46] who made notice of this transformation without many properties. Benedetto noted many more properties with proofs at [36], pages 348-350, among of them (some not mentioned above):
- p is a negative similarity
- p transforms the reference quadrangle into the quadrangle of the pedal centers
- p transforms the quadrangle of the circumcenters into the quadrangle of the ninepoint centers, and therefore
- p interchanges the asymptotic points of QA-Co2
- there is a fixed point of p: P
- p is the commutative product of a reflection on a line through P and a homothety centered in P
- the homothety coefficient equals 2 cos α , where α is the angle formed by the asymptotes of QA-Co1 (this holds for convex quadrangles; a similar formula holds for the non-convex case).
- Construction:
- Given any quadrangle A1A2A3A4 and a generic point Z.
- Reflect Z in two opposite sides of the quadrangle and take the midpoint, say M12,34 =midpoint (ZA1A2 , ZA3A4). Define similarly M13,24 and M14,23.
- Then p(Z) is the circumcenter of the triangle M12,34M13,24M14,23.
1st coordinate QA-Tf3 in CT-notation, given point (u:v:w) to be transformed:
a2 (p r v + q r v + p q w + q r w) + b2 p (r u + r v – q w) + c2 p (q u + q w – r v)
1st coordinate QA-Tf3 in DT-notation, given point (u:v:w) to be transformed:
a2 (-p2 u – p2 v + r2 v – p2 w + q2 w) + b2 p2 (u + v) + c2 p2 (u + w)
Properties:
-
- The circle described in the construction of QA-Tf3(P) is also the locus of QA-Tf6 wrt a pencil of lines through random point P.
- Reflect some random point P in two opposite sides of the quadrangle and let M12,34 be their midpoint of these reflections. Define similarly M13,24 and M14,23.
- Then QA-Tf3(P) is the circumcenter of the triangle M12,34M13,24M14,23 and its circumcircle coincides with the circle described in the initial construction of QA-Tf3.
- The circle described in the construction of QA-Tf3(P) is also used in the construction of 5P-s-Tf3.
- QA-Tf6(Lp) will be a point on the circle described in the construction of QA-Tf3(P) for any line Lp through P. See [34], Ngo Quang Duong, message #2745.
Examples of QA-Orthopoles
The following table lists QA-Orthopoles of several QA-/QG-/QL-Points
| QA-/QG-/QL-Points | QA-Orthopole |
|---|---|
| QA-Points | |
QA-P1: Quadrangle Centroid |
Midpoint (QA-P1, QA-P23) |
QA-P2: Euler-Poncelet Point |
QA-P23: Inscribed Square Axes Crosspoint |
QA-P3: Gergonne-Steiner Point |
QA-P1: Centroid |
QA-P4: Isogonal Center |
QA-P2: Euler-Poncelet Point |
QA-P6: Parabola Axes Crosspoint |
Midpoint (QA-P2, QA-P23) |
QA-P7: QA-Nine-point-Center Homothetic Center |
Point on Line QA-P8.QA-P23 ( 2 : 1) |
QA-P8: Midray Homothetic Center |
QA-P7: QA-Nine-point Center Hom.Center |
QA-P12: Orthocenter QA-Diagonal Triangle |
QA-P11: Circumcenter QA-Diag. Triangle |
QA-P32: Centroid of Circumcenter Quadrangle |
QA-P2.QA-P7 ∧ QA-P1.QA-P32 |
QA-P33: Centroid of Orthocenter Quadrangle |
Point on Line QA-P23.QA-P33 (–1 : 3) |
QA-P36: Complement QA-P30 wrt QA-DT |
Midpoint (QA-P11, QA-P23) |
QA-P42: QA-Orthopole Center |
QA-P42: QA-Orthopole Center |
| QG-Points | |
QG-P1: Diagonal Crosspoint |
Point on Newton Line (QL-L1) |
QG-P5: 1st QG-Quasi Circumcenter |
QG-P7: 1st QG-Quasi Nine-point Center |
QG-P17: Projection QG-P1 on QG-L1 |
Midpoint (QG-P1, QG-P18) |
| QL-Point | |
QL-P1: Miquel Point |
Point on Newton Line (QL-L1) |
The following table lists interesting QA-Orthopoles of several QG-/QL-Lines & Circles:
| QG-/QL-Lines & Circles | QA-Orthopole |
|---|---|
| QG-Line | |
Line QG-P1.QL-P1 |
QL-L1: Newton Line |
| QL-Circles | |
QL-Ci5: Plücker Circle |
Circle through QL-P5 (Center of QL-Ci5) |
QL-Ci6: Dimidium Circle |
Circle through QA-P1 |
Estimated human page views: 1338
