CU-12P1 Harmonic Polar Crosspoints
Let P1, …, P12 be the 12 mutual intersection points of the Harmonic-Polars L1, …, L9 (see CU-9L1).
They are a kind of duals with the 12 flexlines (CU-12L1) passing through the 9 flexpoints (CU-9P1).
The 9 Flexpoints (3 of them real points) lie on 12 Flexlines (4 of them real lines).
The 9 Harmonic Polars (3 of them real lines) intersect in 12 Harmonic-Polar-Crosspoints (4 of them real points).
The 12 Harmonic-Polar-Crosspoints and the 12 Flexlines have a Pole/Polar-relationship wrt the CU-Pi-Polar Conic.
Note that there are always 3 real Harmonic Polars and 6 imaginary Harmonic Polars.
Note also that there is 1 real Harmonic Polar Crosspoint, being the common intersection point of the 3 real Harmonic Polars. Beyond that there are three other real Harmonic Polar Crosspoints, each lying on just 1 real Harmonic Polar and 2 imaginary Harmonic Polars. The remaining Harmonic Polar Crosspoints are all imaginary points, each lying on three imaginary Polars.
The set of 9 Harmonic Polars (real or imaginary) are structured in a point-network as follows:
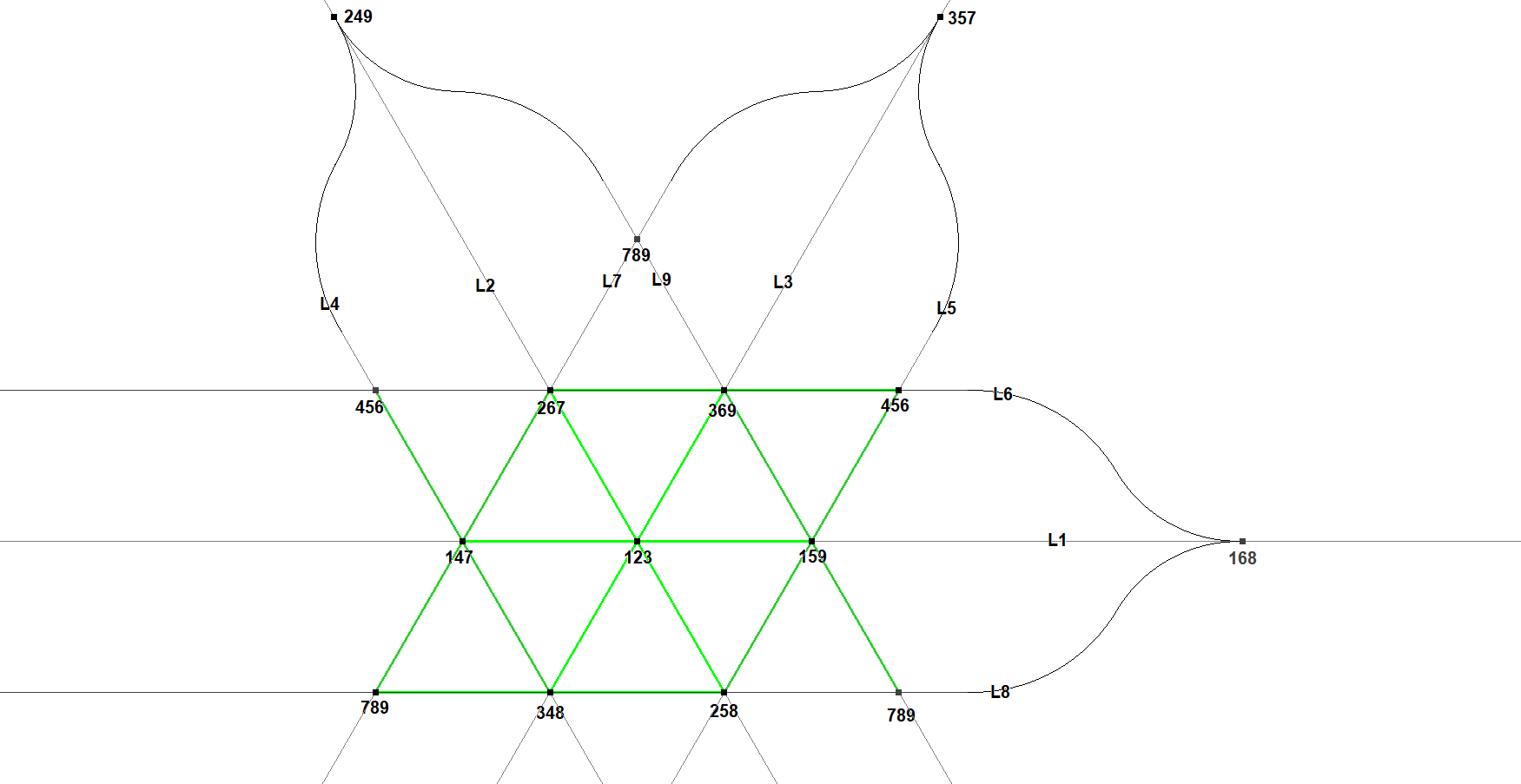
CU-9L1 Harmonic Polars-scheme of intersection points-02.fig
It is a spacious triangular net characterized by the following features:
- there are effectively 9 lines, each line contains 4 points
- there are effectively 12 points, each point is passed by 3 lines
In order to make intersections appear like they (according to calculations) do:
- lines repeat in parallel lines skipping 2 other lines
- points repeat as vertices of larger triangles, each side being three times longer than the smaller ones, (for example find three versions of point 789)
- parallel lines also converge in one point.
That’s all because this is a system of points and lines in the complex projective plane being projected to a noncomplex affine plane.
There is a relationship with the Flexpoint/Flexline-Network. See CU-12L1 and QPG#2410.
Estimated human page views: 114
