nP-n-L2: nP-LSD Line
The nP-LSD line is the line with the Least Sum of Squared Distances of the vertices of an n-Point to this line.
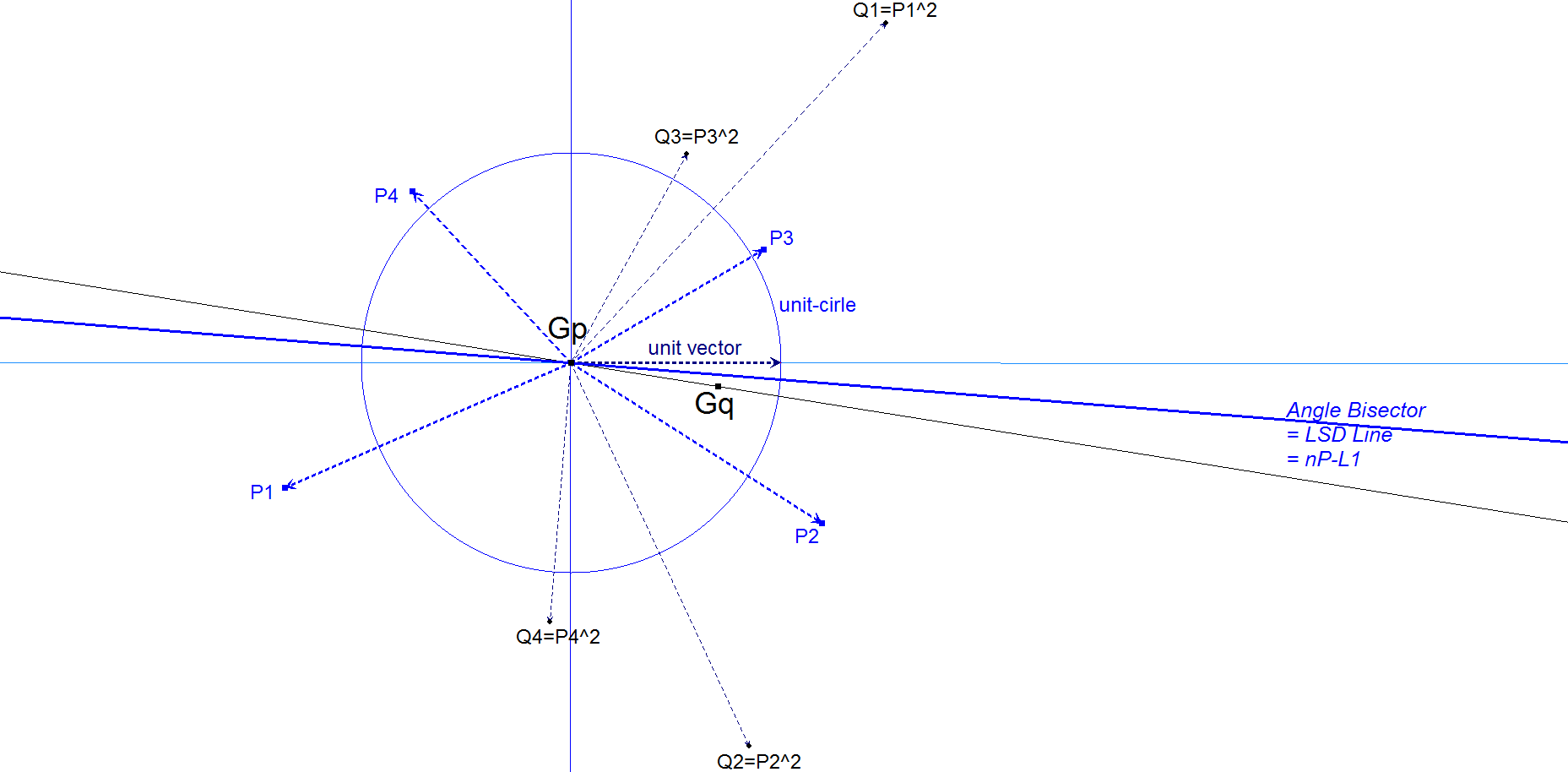
Construction
Choose a random couple of perpendicular lines intersecting in the Centroid Gp = nP-P1 as axes of the Complex plane.
Let the complex numbers zi = xi + i.yi represent the vertices of the n-Point.
The centroid of the vertices is the point nP-P1 where z = 0.
The centroid of the points represented by zi2 is a 2nd point Gq = nP-Px.
Draw the line nP-P1.nP-Px (depending of the chosen axes).
The searched LSD Line is the bisector of the angle between this line nP-P1.nP-Px and the x-axis of the xi (this last line is independent of the chosen axes).
See messages Benedetto Scimemi and Bernard Keizer at [34], QFG#1585, #1590, #1593.
Correspondence with ETC/EQF
In a 3-Point-configuration
3P-n-L2 = Main Axis of the Steiner CircumEllipse
In a 4-Point-configuration
Estimated human page views: 465
