QA-Ci2: QA-Medial Circle Diagonal Triangle
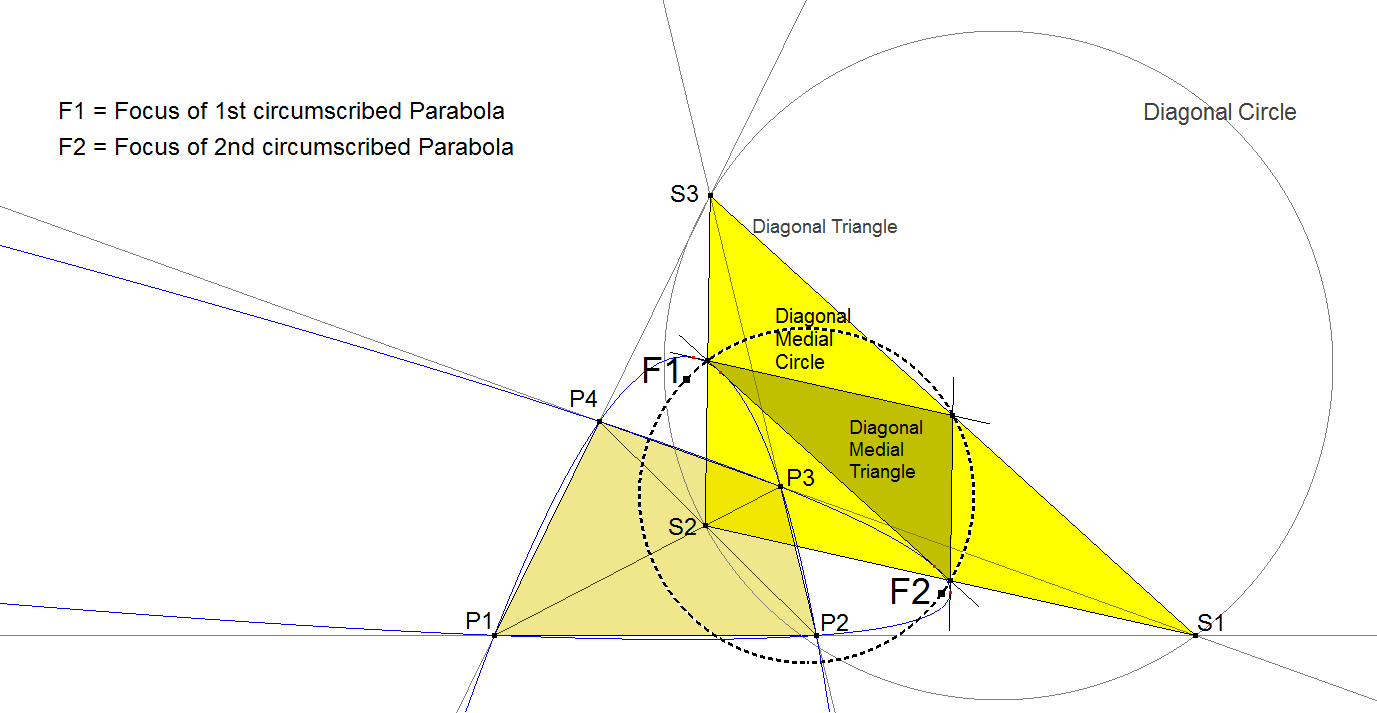
The Diagonal Medial Circle is the circumcircle of the Medial Triangle (MT) of the Diagonal Triangle (DT) of a Quadrangle.
It is also the Nine-point Circle (or also called Euler Circle) of the QA-Diagonal Triangle.
Equation CT-notation:
(x + y + z) (TMX x + TMY y + TMZ z) + 2 TXYZ (a2 y z + b2 x z + c2 x y) = 0
where:
TMX = qr(a2 qr(p+q)(r+p) – b2 pr(p+q)(q+r) – c2 pq(r+p)(q+r)) – 2 q2r2 (a2 qr+b2 rp+c2 pq)
TMY = pr(–a2qr(p+q)(r+p)+b2 pr(p+q)(q+r) – c2 pq(r+p)(q+r)) – 2 r2p2 (a2 qr+b2 rp+c2 pq)
TMZ = pq(–a2qr(p+q)(r+p)–b2pr(p+q)(q+r) + c2 pq(r+p)(q+r)) – 2 p2 q2(a2 qr+b2 rp+c2 pq)
TXYZ = 2 pqr (p+q) (q+r) (r+p)
Equation DT-notation:
SA x2 + SB y2 + SC z2 – c2 x y – b2 x z – a2 y z = 0
Properties
- These points lie on QA-Ci2:
- QA-P13 is the center of the Medial Circle.
Estimated human page views: 648
