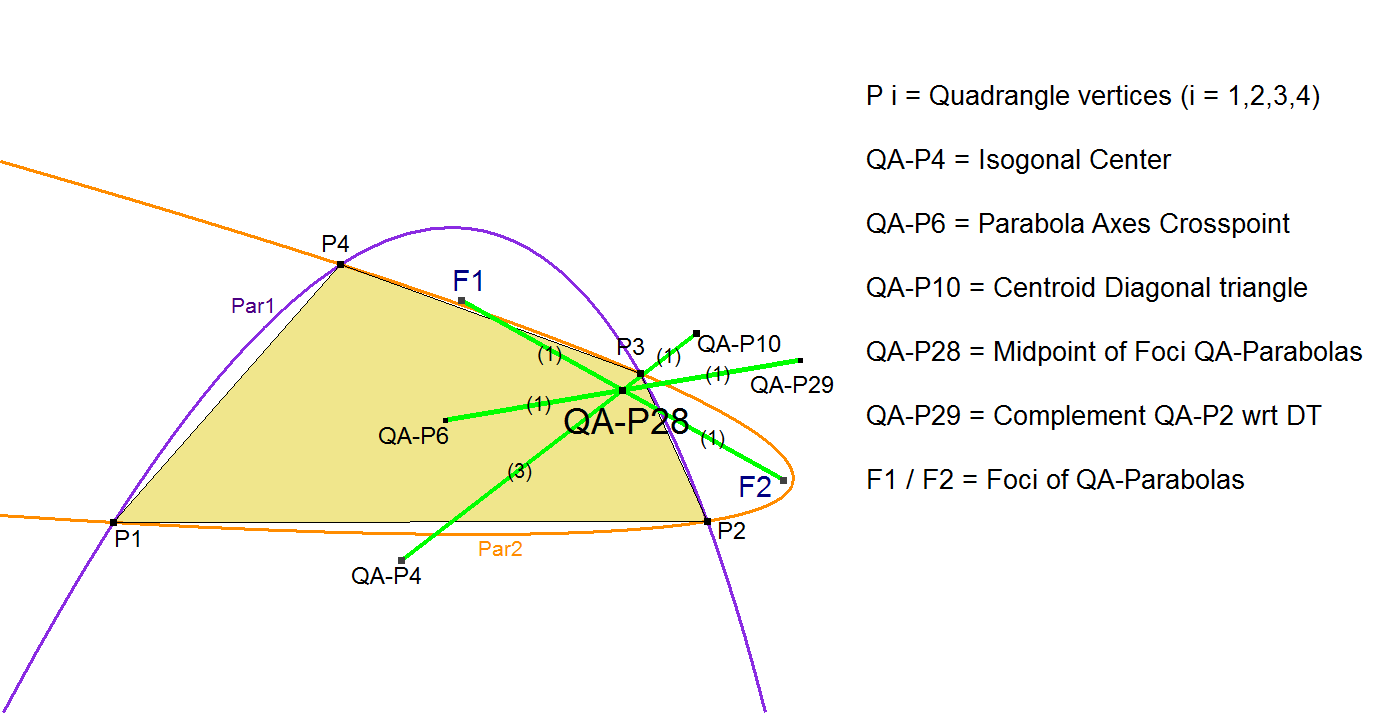
QA-P28: Midpoint of the foci of the QA-Parabolas

QA-P28 is the Midpoint of the foci F1 and F2 of the pair of circumscribed QA-Parabolas (QA-2Co1) .

Because these parabolas only can be constructed when the Reference Quadrangle is not concave a better definition of this point is: “the point on the line QA-P4.QA-P10 such that its distance relation to these points is resp. 3 : 1”.

But because the property related to the parabolas is much more appealing this point has been called after its primary function.

It also can be reasoned that in a concave quadrangle this point represents the Midpoint of the foci of the imaginary parabolas.

1st CT-Coordinate

(q + r) (-a⁴ q r (p + q) (p + r) (3 p² + 2 p q + 2 p r + q r)

– p² (q + r) (2 p + q + r) (c⁴ p q + b⁴ p r + (b² – c²)² q r)

+ p q r (5 p² + 3 p q + 3 p r + q r) (a² b² (p + q) + a² c² (p + r)))

1st DT-Coordinate

-2 b² c² p⁴ – a² c² q⁴ – a² b² r⁴ + c² (3 S_C – S_B) p² q² + b² (3 S_B – S_C) p² r² + a² ( c² + b²) q² r²

Properties

• QA-P28 lies on these QA-lines:
  • QA-P4.QA-P10 (3 : 1)
  • QA-P6.QA-P29 (1 : 1 => QA-P28 = Midpoint QA-P6.QA-P29)
• QA-P28 = projection of QA-P13 (Nine-point Center DT) on F1.F2
• QA-P28 = Complement of the Isogonal Conjugate of QA-P3 wrt QA-DT
• QA-P28 = QA-Centroid of Quadrangle S1.S2.S3.QA-P4 (Si = vertices QA-DT)
• QA-P28 = QA-Centroid of Quadrangle QA-P2.QA-P3.QA-P4.QA-P20.

Estimated human page views: 484