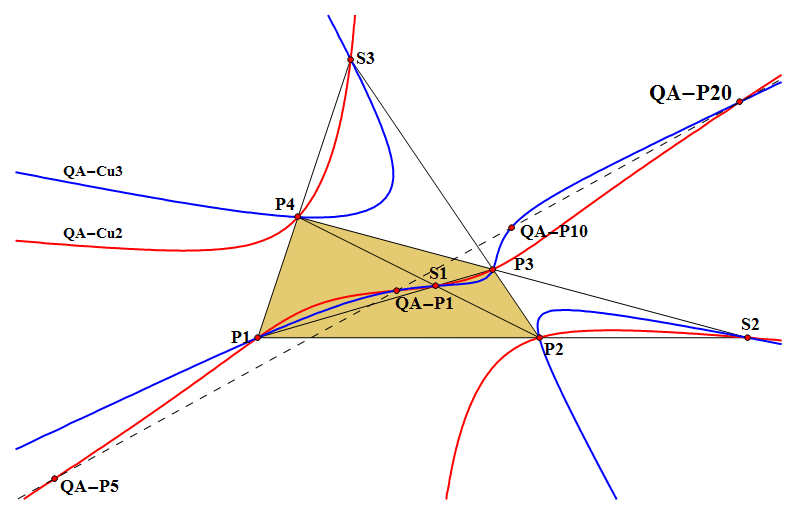
QA-P20: Reflection of QA-P5 in QA-P1
QA-P20 is the Reflection of QA-P5 (Isotomic Center) in QA-P1 (QA-Centroid).
1st CT-coordinate
(q + r) (2 p + q + r) (p2 + p q + p r – q r)
1st DT-coordinate
1 / (-p2 + q2 + r2)
Properties
- QA-P20 lies on these QA-lines:
- QA-P1.QA-P5 (-1 : 2 => QA-P20 = Reflection of QA-P5 in QA-P1)
- QA-P3.QA-P29 ( 1 : 1 => QA-P20 = Reflection QA-P3 in QA-P29)
- QA-P11.QA-P37 (-1 : 2 => QA-P20 = Reflection QA-P37 in QA-P11)
- QA-P21.QA-P31 (2 : -1 => QA-P20 = Reflection of QA-P21 in QA-P31)
- QG-P15.QG-P2 (2 : -1 => QA-P20 = Reflection of QG-P15 in QG-P2)
- QA-P34.QA-P35 (5 : -3)
- QA-P20 is also he Reflection of:
- QA-P20 lies on the line QA-P1.QA-P5.QA-P10 in harmonic position:
QA-P5.QA-P1 : QA-P1.QA-P10 : QA-P10.QA-P20 = 3 : 1 : 2. - QA-P20 is the Involutary Conjugate (see QA-Tf2) of QA-P1.
- QA-P20 is the Isotomic Conjugate of QA-P19 wrt the QA-Diagonal Triangle.
- QA-P20 is the Anticomplement of QA-P1 wrt the QA-Diagonal Triangle.
- QA-P20 is the Antipode of QA-P3 in the QA-DT-P3-P12 Orthogonal Hyperbola (QA-Co4).
- QA-P20 lies on the Conic QA-Co5.
- QA-P20 lies on the Cubics QA-Cu2, QA-Cu3 and QA-Cu5.
- QL-P8 is the Centroid of the QL-Triangle formed by the 3 QL-versions of QA-P20 (note Eckart Schmidt).
- QA-P20 lies on the line connecting the Involutary Conjugates (QA-Tf2) of QG-P4 and QG-P8 (ratio 2: 1).
This line also passes through QG-P1. - QA-P20 is the common point of these 3 lines:
L1= line parallel to M12.M34 through P1.P2 ^ P3.P4,
L2= line parallel to M13.M24 through P1.P3 ^ P2.P4,
L3= line parallel to M14.M23 through P1.P4 ^ P2.P3,
where Mij = midpoint(Pi,Pj) for (i,j) ∈ (1,2,3,4)
(Seiichi Kirikami, September 13, 2012). - QA-P20 is the Perspector of the QG-P2 Triple Triangle and the QG-P15 Triple Triangle (see QA-Tr-1).
- QA-P20 is the Orthology Center of the QG-P1 Triple Triangle wrt the Triple triangles of QG-P5/QG-P10/QL-P2.
See QA-Tr-1. See [34], QFG#962,#963.
Estimated human page views: 613
