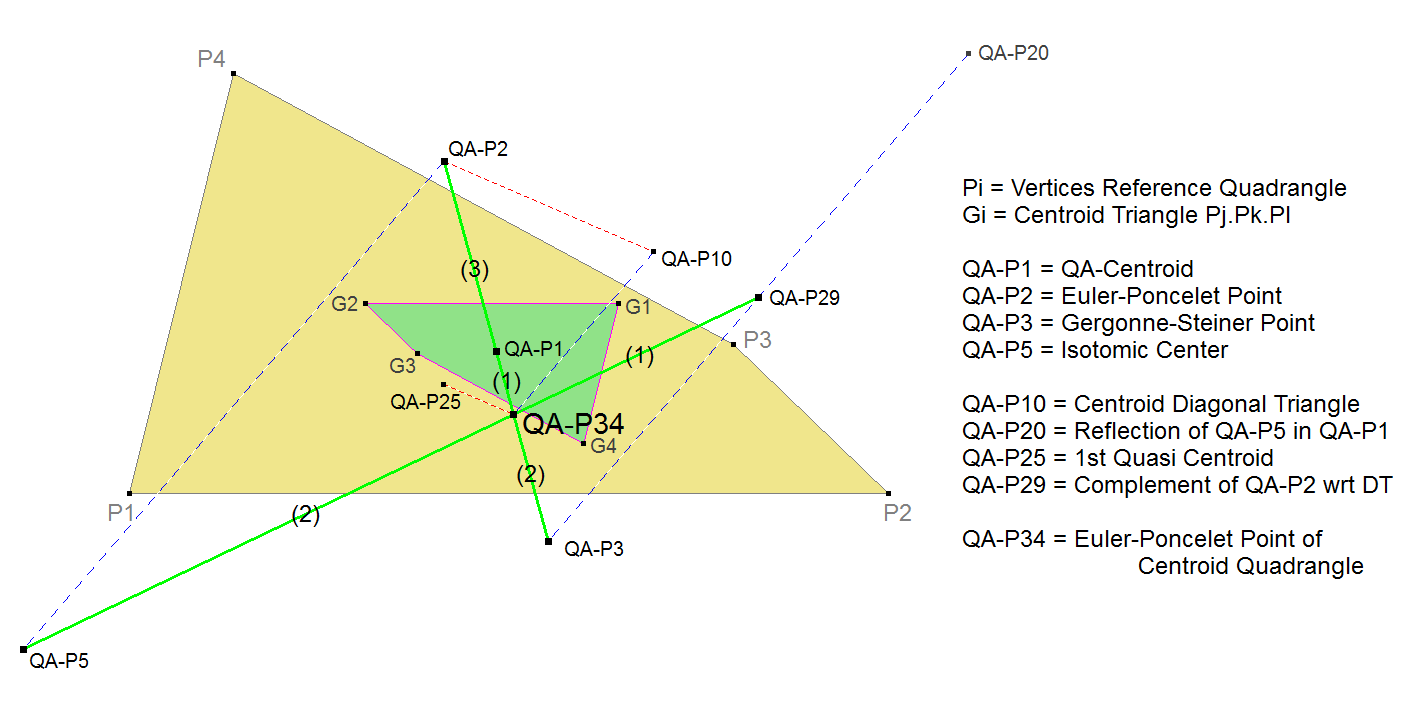
QA-P34: Euler-Poncelet Point of the Centroid Quadrangle

QA-P34 is the Euler-Poncelet Point of the quadrangle formed by the Centroids of the Component Triangles of the Reference Quadrangle.

The Euler-Poncelet point also can be constructed in similar Quadrangles:

• • QA-P1 also is Euler-Poncelet Point of the Nine-point Center Quadrangle.
  • QA-P2 also is Euler-Poncelet Point of the Orthocenter Quadrangle.
  • QA-P3 also is Euler-Poncelet Point of the Circumcenter Quadrangle.

Surprisingly now QA-P1, QA-P2, QA-P3 and QA-P34 have mutual distance ratios similar to the corresponding points in the Triangle Environment on the Euler Line.

This point was contributed by Eckart Schmidt (12/18/2011).

1st CT-Coordinate

2 a⁴ q r (p + q) (p + r) (2 p + q + r)

+ b⁴ p r (p + q) (q + r) (3 p + q + r)

+ c⁴ p q (p + r) (q + r) (3 p + q + r)

+ b² c² p (q + r) ((p + q) (q + r) (r + p) – 3 q r (2 p + q + r))

– a² b² p r (p + q) (3 q (p + q) + (4 q + r) (p + r))

– a² c² p q (p + r) (3 r (p + r) + (4 r + q) (p + q))

1st DT-Coordinate

((p² + q² + r²)² – 4 (p⁴ + q² r²)) (-b² p² + a² q²) (c² p² – a² r²)

+ 4 p² (-p² + q² + r²) (-c² q² + b² r²) ((-b² p² + a² q²) + (c² p² – a² r²))

Properties

• • • QA-P34 lies on these QA-lines:
      • QA-P1.QA-P2          (-1 :  4)
      • QA-P5.QA-P29        ( 2 :  1)
      • QA-P20.QA-P35      ( 5 : -2)
    • The distance ratios between points QA-P3, QA-P34, QA-P1, QA-P2 are 2 : 1 : 3.
    • QA-P34.QA-P10 // QA-P2.QA-P5 // QA-P3.QA-P20.
    • QA-P34.QA-P25 // QA-P2.QA-P10.
    • QA-P34 lies on the circle defined by the 3 QA-versions of QG-P4 (note Eckart Schmidt).
    • QA-P34 is the Orthology Center of the QG-P8 Triple Triangle wrt the Triple triangles of QG-P7/QG-P9/QL-P6. See QA-Tr-1.

Estimated human page views: 532