← Previous Next →

QG-P12: Inscribed Harmonic Conic Center

The Inscribed Harmonic Conic Center is the Center of the Inscribed Harmonic Conic QG-Co1. This conic touches the sidelines of the Quadrigon in their perspective midpoints.

See picture below.

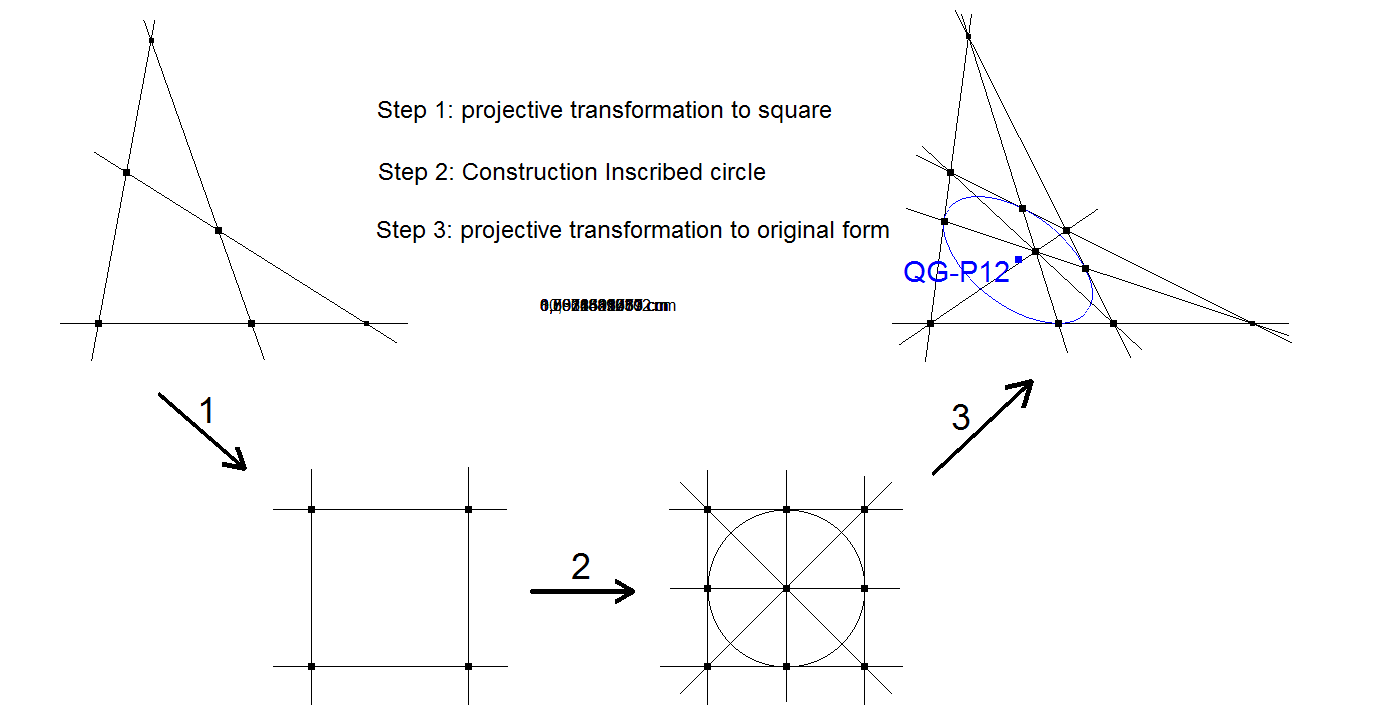
Infovisual QG-P12-infovisual-cvt-01.png
CT-Coordinates QG-P12 in 3 QA-Quadrigons

(p(2p+q+r) : q(p-r) : r(p-q))

(p(r-q) : q (r-p) : r(p+q+2r))

(p(q-r) : q(p+2q+r) : r(q-p))

CT-Coordinates QG-P12 in 3 QL-Quadrigons

( m + n : -2l + n : -2l + m)

(-2m + n : l + n : -2m + l)

( -2n + m : -2n + l : l + m)

CT-Area of QG-P12–Triangle in the QA-environment

p q r (p + q)(p + r)(q + r) Δ / ((p2 + p q + p r – q r) (p q + q2 – p r + q r) (p q – p r – q r – r2))

CT-Area of QG-P12–Triangle in the QL-environment

0   (points are collinear on Newton Line)

–

DT-Coordinates QG-P12 in 3 QA-Quadrigons

(-p2 : q2 : r2)

( p2 : -q2 : r2)

( p2 : q2 : -r2)

DT-Coordinates QG-P12 in 3 QL-Quadrigons

(-2 m2 n2 : l2 n2 : l2 m2)

( m2 n2 : -2 l2 n2 : l2 m2)

( m2 n2 : l2 n2 : -2 l2 m2)

DT-Area of QG-P12–Triangle in the QA-environment

(-2 S p2 q2 r2) / ((-p2+q2+r2) (p2+q2-r2) (p2-q2+r2))

DT-Area of QG-P12–Triangle in the QL-environment

0   (points are collinear on Newton Line)

Properties
  • QG-P12 is the fourth harmonic point of QG-P2 (Midpoint 3rd Diagonal) on the Newton Line (QL-L1) wrt the midpoints of the diagonals (note Eckart Schmidt).
  • QG-P12 is collinear with QG-P1, QG-P13, QA-P16, QL-P13 on QG-L2.
  • QG-P12 is collinear with QA-P42 and QL-P26.
  • The triangle formed by the 3 QA-versions of QG-P12 is perspective with the QA-Diagonal Triangle. Their Perspector is QA-P16 (QA-Harmonic Center).
  • The triangle formed by the 3 QL-versions of QG-P12 is a flat Triangle (the 3 vertices are collinear on the Newton Line QL-L1) and is perspective with the QL-Diagonal Triangle. Their Perspector is QL-P13 (QL-Harmonic Center).
  • QG-P12 is the intersection point of the Trilinear Polars of QG-P13 as well as QL-P13 wrt the QA-Diagonal Triangle and the QL-Diagonal Triangle (note Eckart Schmidt).
  • The Involutary Conjugate (QA-Tf2) of QG-P12 is the Reflection of QG-P1 in QG-P2.
  • The involutary Conjugate (QA-Tf2) of QG-P12 lies on the line QG-P14.QG-P15.QA-P5.
  • The Involutary Conjugates (QA-Tf2) of QG-P12 and QG-P13 both lie on the line QG-P1.QG-P2.QA-P10.
  • The 3 QA-versions of QG-P12 lie on the QA-circumconic through QA-P1 (Eckart Schmidt, October 9, 2013). See [34], QFG # 286,287.


Estimated human page views: 585

Scroll naar boven