← Previous Next →

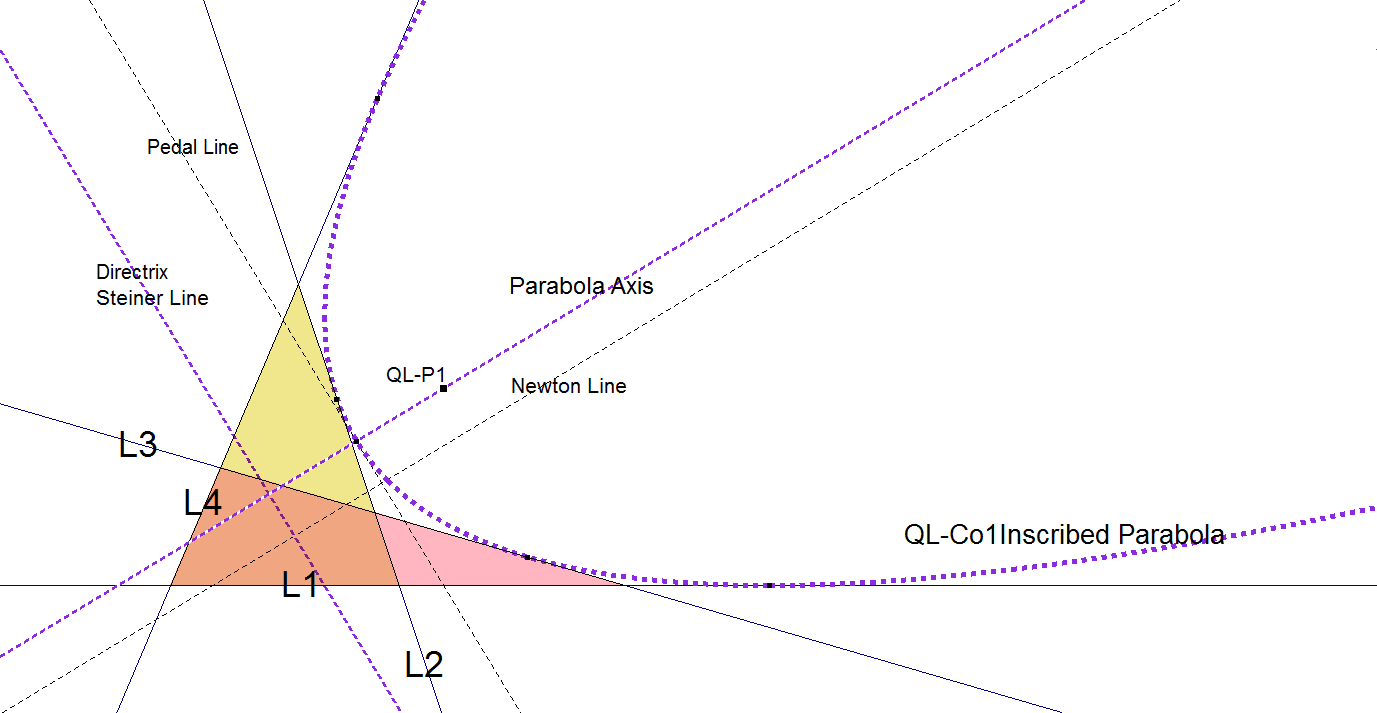
QL-Co1: Inscribed Parabola

The inscribed Parabola is the unique parabola that can be inscribed within a Quadrilateral.

This parabola is also described by Bernard Keizer in [43] and [34], QFG message # 504.

Infovisual QL-Co1-infovisual-cvt-01.png
Equation CT-notation

l2 (m – n)2 x2 – 2 m n (l – m)(n – l ) y z

+ m2 (l – n)2 y2 – 2 n l (l – m)(m – n) x z

+ n2 (l – m)2 z2 – 2 l m (n – l)(m – n) x y = o

1st CT-coefficient Axis Parabola

l (m – n) (c l m + b l n – b m n – c m n) (c l m – b l n + b m n – c m n)

Infinity point Axis CT-notation

( l (m–n) : m (n – l) : n (l – m))

Points of tangency with L1, L2 , L3, L4 in CT-notation

( 0 : n (l – m) : m (n – l))

( n (l – m) : 0 : l (m – n))

( m (n – l) : l (m – n) : 0 )

(m n (m – n) : n l (n – l) : l m (l – m))

–

Equation DT-notation

x2/(m2-n2) + y2/(-l2+n2) + z2/(l2-m2) = 0

1st DT-coefficient Axis Parabola

(l2-m2) (l2-n2) ((l2-n2) SB+(l2-m2) SC)

Infinity point Axis DT-notation

( m2-n2 : -l2+n2 : l2-m2 )

Points of tangency with L1, L2 , L3, L4 in DT-notation

(-l (m2 – n2) : m (l2 – n2) : (l2 – m2) n)

( l (m2 – n2) : -m (l2 – n2) : (l2 – m2) n)

( l (m2 – n2) : m (l2 – n2) : -(l2 – m2) n)

( l (m2 – n2) : m (l2 – n2) : (l2 – m2) n)

Properties
  • QL-Co1 is the only parabola inscribed in the quadrilateral (see [4] page 51).
  • QL-Co1 is the 5th Line Conic of QL-L3 (see QL-Co-1).
  • The Focus is QL-P1 the Miquel Point.
  • The Directrix is QL-L2 the Steiner Line.
  • The Axis of QL-Co1 is parallel to QL-L1, the Newton Line.
  • QL-Co1 is also an inscribed parabola of the QL-Medial Triangle (the medial triangle of the QL-Diagonal Triangle).
  • The Nine-point Conics of the 3 Quadrigons of a Quadrilateral have 3 common points which constitute triangle QL-Tr2. The Inscribed Parabola of the quadrilateral is also an inscribed parabola of QL-Tr2.
  • QL-P1 lies on the Polars (see [13], Polar) of QL-P2, QL-P7, QL-P9 wrt QL-Co1.
  • QL-P8 lies on the Polar (see [13], Polar) of QL-P12 wrt QL-Co1 and vice versa.
  • Let T1, T2, T3, T4 be the points of tangency of QA-Co1 with the basic lines of the Reference Quadrilateral. Now the QL-Diagonal Triangle of the Reference Quadrilateral and the QA-Diagonal Triangle of the Quadrangle T1.T2.T3.T4 are identical.
  • The QL-Tf2-image of the QL-Co1-polar of a point P contains P. See [34], Eckart Schmidt, QFG-message #1666.


Estimated human page views: 956

Scroll naar boven