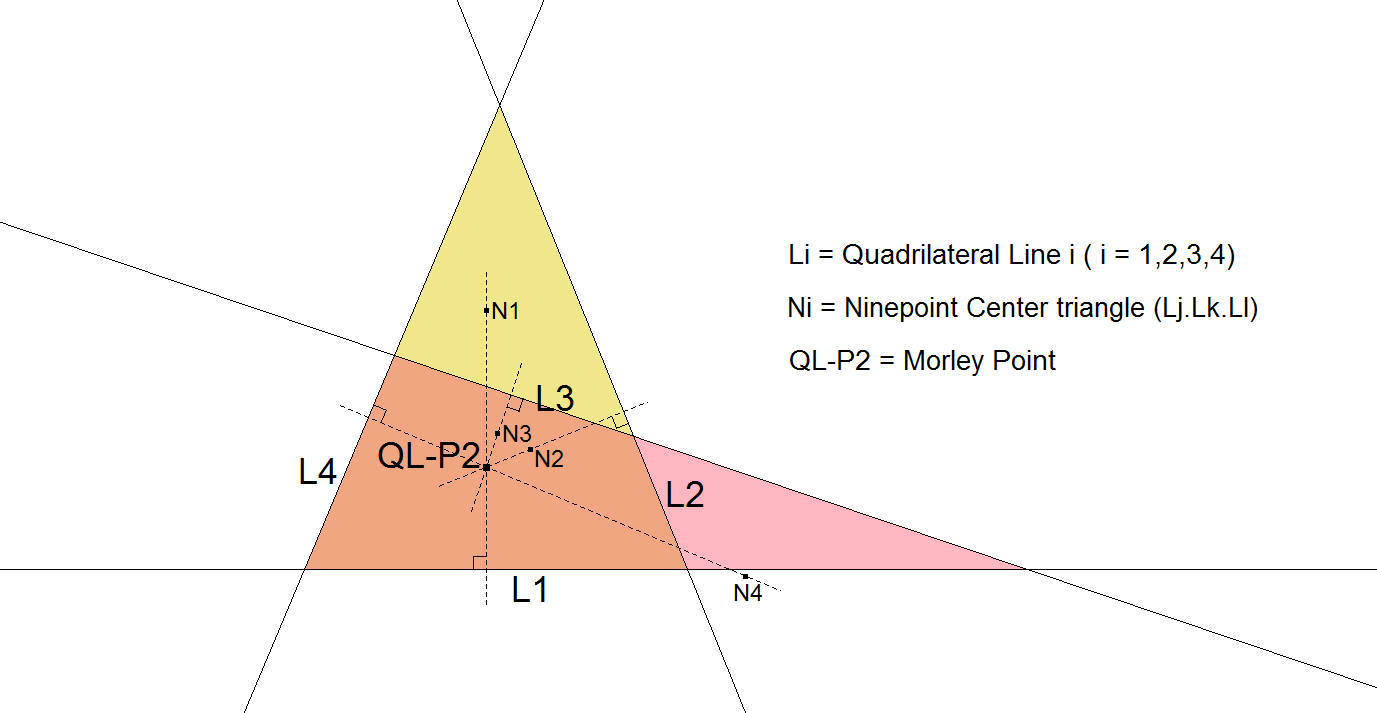
QL-P2: Morley Point

Let Ni be Nine-point Center of triangle LjLkLl.

Let Lpi be the perpendicular line of Ni at Li.

Now all perpendicular lines Lpi (i=1,2,3,4) concur in one point QL-P2.

This point was found by Frank Morley naming it the Second Orthocenter in his document [49], paragraph 3. It is described as a recursive point in an n-Line. In his document he uses the letter “h” for this point.

QL-P2 is also mentioned by J.W. Clawson in [31, pp. 40 and 41] as the “mean center of gravity of equal masses placed at H1, H2, H3, H4”, where H1, H2, H3, H4 are the orthocenters of the Component Triangles of the Reference Quadrilateral.

1^st CT-coordinate

+a⁴ l (2 l – m – n) + b² c² (2 l² – 3 l m – 3 l n + 4 m n)

– b⁴ (l – 2 m) (l – n) + a² c² (l² m + l² n – 5 l m n + 2 m² n + l n²) /(m – n)

– c⁴ (l – 2 n) (l – m) + a² b² (l² m + l² n – 5 l m n + 2 m n² + l m²)/(n – m)

1^st DT-coordinate

Sb Sc – (Sb² m² (-l²+n²))/((l²-m²) (m²-n²)) – (Sa Sb m²)/(l²-m²)

– (Sc² n² (l²-m²))/((l²– n² ) (m²-n²)) – (Sa Sc n² )/(l²– n²)

Properties

• QL-P2 lies on these lines:
  • QL-P4.QL-P22        (2 : -1 => QL-P2 = Reflection of QL-P4 in QL-P22)
  • QL-P6.QL-P12        (3 : -2)
  • QL-P7.QL-P9
  • QA-P24.QG-P5       (1 : 1 => QL-P2 = Midpoint QA-P24 and QG-P5)
• QL-P2.QL-P3 = QL-L4 (Morley Line) // Newton Line QL-L1.
• QL-P2.QL-P10 = QL-L6 (Quasi Ortholine).
• d (QL-P2 , QL-P3) = 3 * d (QL-P5 , QL-P12). (d = distance)
• d (QL-P2, QL-L1) = d (OL-P3, QL-L1) = d (OL-P4, QL-L1), where QL-L1=Newton Line.
• The QA-Triangle formed by the 3 QA-versions of QL-P2 is Triangle QA-Tr3 with Centroid QA-P14 and Orthocenter QA-P15.
• QL-P2 is the Centroid of the Triangle formed by the 3 QL-versions of QA-P14 (note Eckart Schmidt).
• QL-P2 is the Centroid of the Orthocenters of the 4 Component Triangles of the Reference Quadrilateral (J.W. Clawson, see [31]).
• QL-P2 is the Orthocenter of QL-Tr2, the triangle formed by the three common points of the 3 QL-versions of the Nine Point Conic QA-Co1 (Benedetto Scimemi, January 19, 2016).
• QL-P2 lies on the Circle defined by the 3 QL-versions of QG-P7 (note Eckart Schmidt).
• The Clawson-Schmidt Conjugates of QL-P2 lies on QL-Ci3 (Miquel Circle).
• QL-P2 (Morley Point) lies on the circumcircle of the triangle formed by the 1st Quasi Nine-point Centers (QG-P7) of the 3 QL-Quadrigons.
• QL-P1 lies on the Polar (see [13], Polar) of QL-P2 wrt QL-Co1.
• QL-P2 is the External Homothetic Center of Morley’s Second Circle (see QL-P30) and the Miquel Circle QL-Ci3. See [49], Theorem 10.
• The QL-P2 Triple Triangle in a Quadrangle is Orthologic wrt all QA-Component Triangles (Seiichi Kirikami, [34], QFG #980, # 982). See QA-Tr-1.
• The QL-P2-Triple Triangle in a Quadrangle is perspective with the QL-P3-Triple Triangle as well as the QL-P29-Triple Triangle in a Quadrangle with perspector QA-P15.

Estimated human page views: 617