← Previous Next →

QL-L6: Quasi Ortholine

The Quasi Ortholine originates from the centers from 3 parallelograms that are collinear on the Quasi Ortholine.

These parallelograms are each constructed from the 3 Quadrigons of the Reference Quadrilateral.

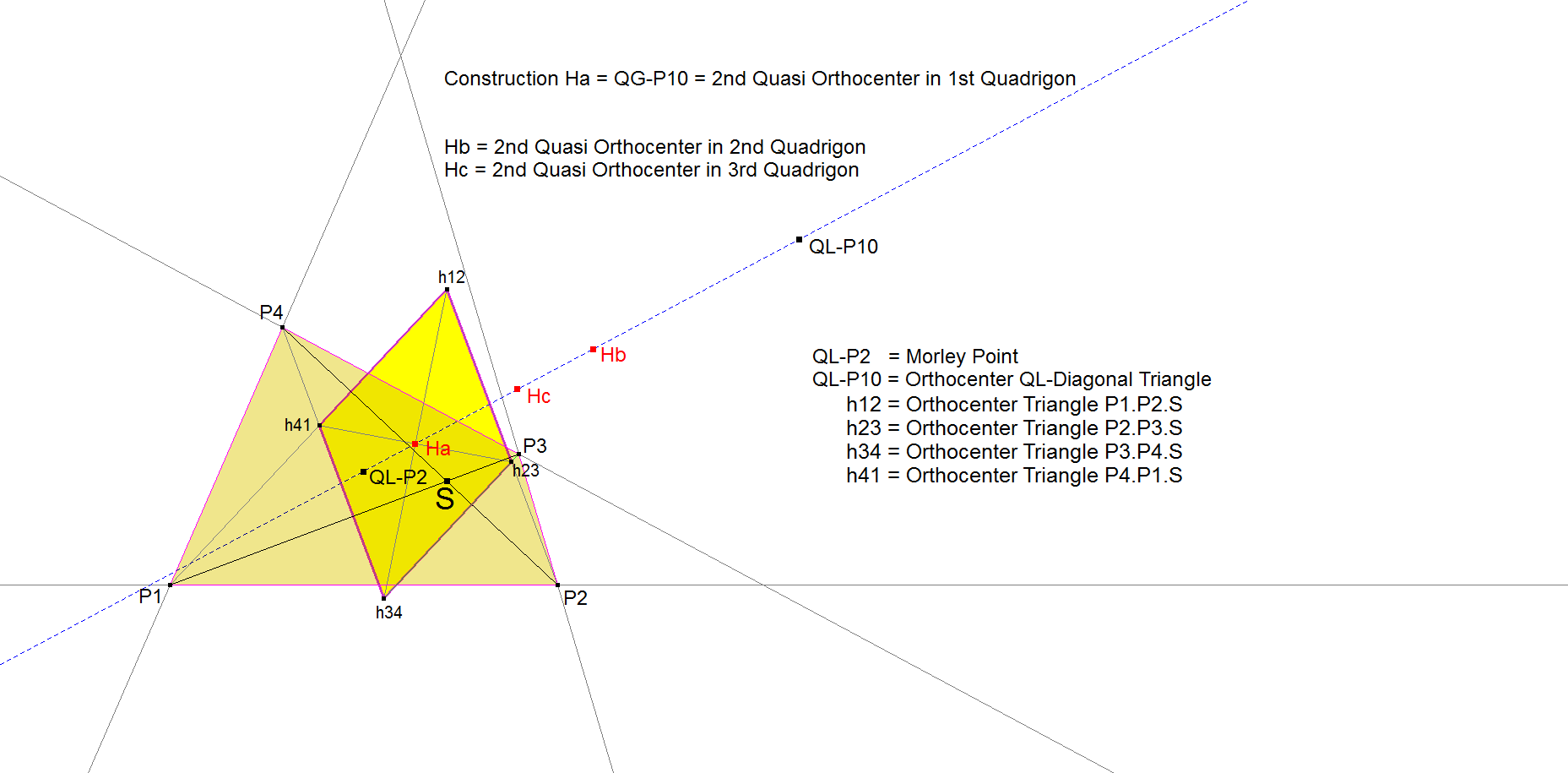
Let P1.P2.P3.P4 be a Quadrigon and S be the intersection point of the diagonals:

S = P1.P3 ^ P2.P4

h ij = Orthocenter in Triangle S.Pi.Pj (i and j consecutive nrs in the cycle 1,2,3,4)

Now h12.h23.h34.h41 is a parallelogram.

It is remarkable that:

  • line h41.h12 passes through P1,
  • line h12.h23 passes through P2,
  • line h23.h34 passes through P3,
  • line h34.h41 passes through P4.

The parallelogram has Center Ha = QG-P10 = 2nd Quasi Orthocenter.

Do this for all 3 Quadrigons in a Quadrilateral.

This gives centers Ha, Hb, Hc. These centers Ha, Hb, Hc are collinear.

The line through Ha, Hb, Hc also passes through QL-P2 (Morley Point) as well as QL-P10 (Orthocenter of the QL-Diagonal Triangle) in the Quadrilateral.

The line is called Quasi Ortholine because it passes through the 2nd Quasi Orthocenters of the 3 component Quadrigons of the Reference Quadrangle.

Infovisual QL-L6-infovisual-cvt-01.png
Infovisual QL-L6-infovisual-cvt-02.png
1st CT-coefficient

l m n (b2 (l – m) – c2 (l – n)) + l (m – n) (l m + l n – m n) SA

1st CT-Coordinate Infinity point

l m n (a2 (2 l – m – n) – (b2 – c2) (m – n)) – m (l – n) (l m – l n + m n) SB + n (l – m) (l m – l n – m n) SC

1st CT-Coordinate Infinity point of perpendicular line to QL-L6 (very simple coordinates)

l (m – n) (-3 m n + l m + l n)

–

1st DT-coefficient

l2 (m2-n2) SA

1st DT-Coordinate Infinity point

m2 (l2 – n2) SB + n2 (l2 – m2) SC

1st DT-Coordinate Infinity point of perpendicular line to QL-L6 (very simple coordinates)

l2 (m2-n2)

Properties
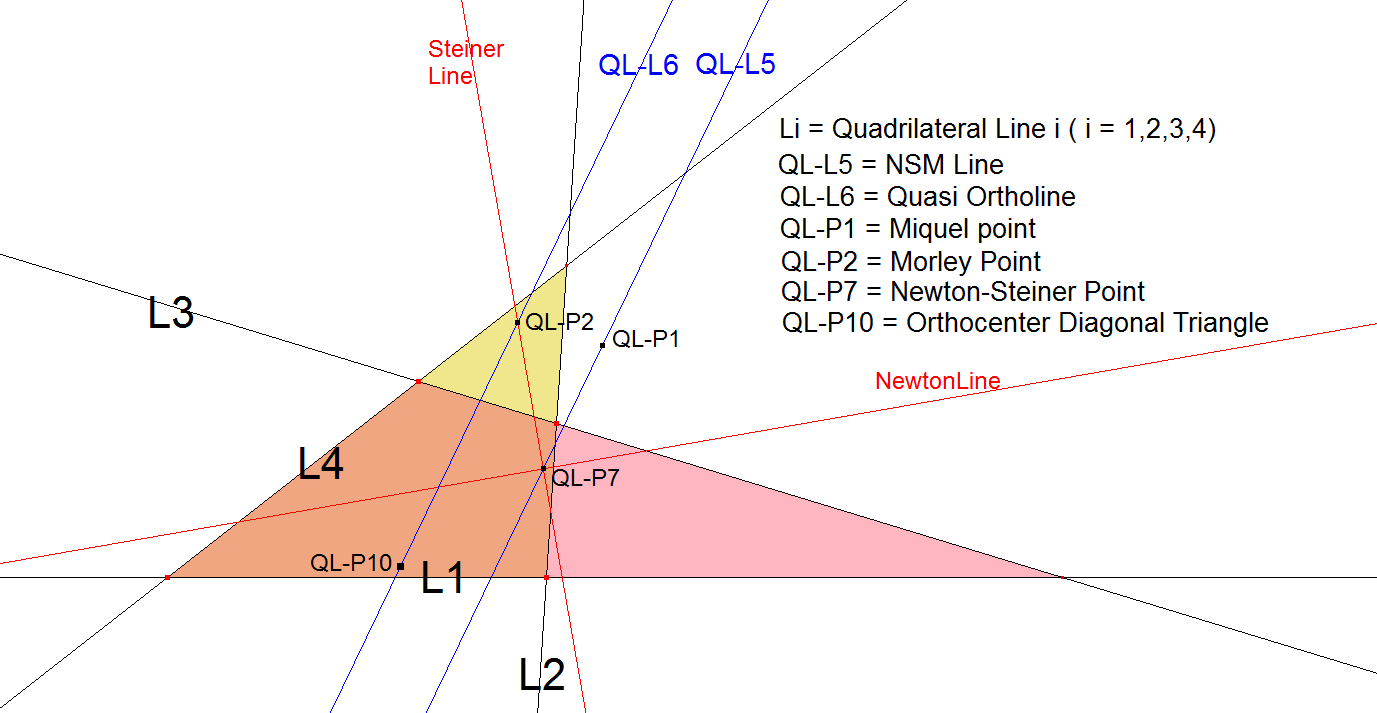
  • QL-L6 passes through QL-P2 (Morley point) and QL-P10 (OrthoCenter QL-Diagonal Triangle)
  • QL-L6 is parallel to QL-L5 (NSM Line)
  • QL-L9 (M3D Line) is perpendicular to QL-L6.
  • The circumcenter of the triangle formed by the 3 QL-versions of QG-P13 lies on QL-L6.
  • The 3 QL-versions of QA-P14 lie on QL-L6 (note Eckart Schmidt).
  • The 3 QL-versions of QG-P10 lie on QL-L6 (note Eckart Schmidt).
  • QL-L6 is the Steiner Line (QL-L2) of the Quadrilateral formed by the lines of the QL-Diagonal Triangle and the Newton Line (QL-L1). See [34], message # 164 and accompanying document “Diagonal Quadrilaterals and Conics through the points S1,S2,S3” page 2 of Bernard Keizer.


Estimated human page views: 555

Scroll naar boven