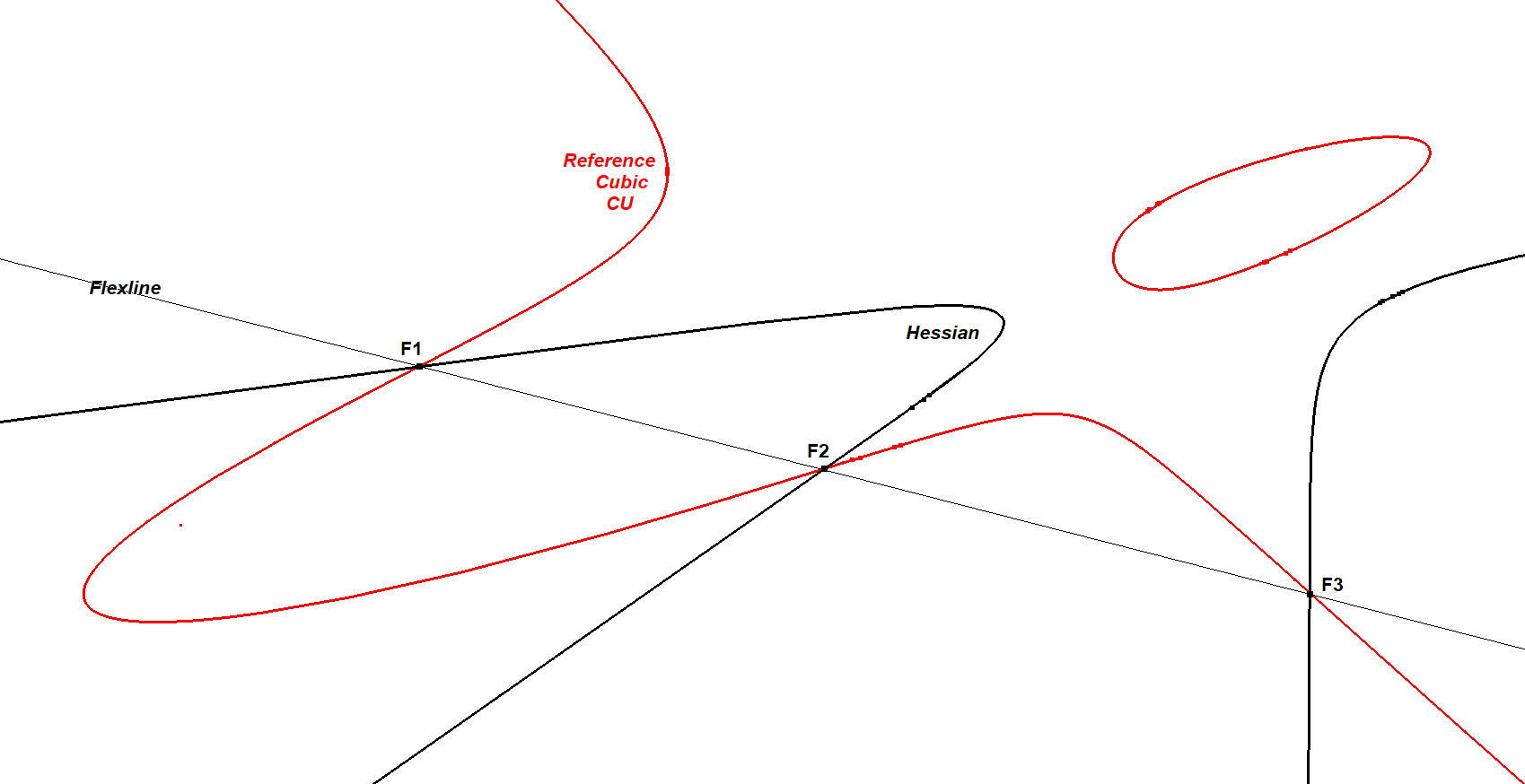
CU-12L1 Set of 12 Flexlines of the Cubic

Like described at CU-9P1, there is a set of 9 Flexpoints on the cubic.

However on any cubic only 3 of these Flexpoints will be real points and they also will be collinear. The other 6 Flexpoints will be imaginary points and there will be 12 Flexlines of which 4 real lines. The other flexlines are imaginary lines.

CU-12L1a Real Flexline-01

Structure of the Flexlines

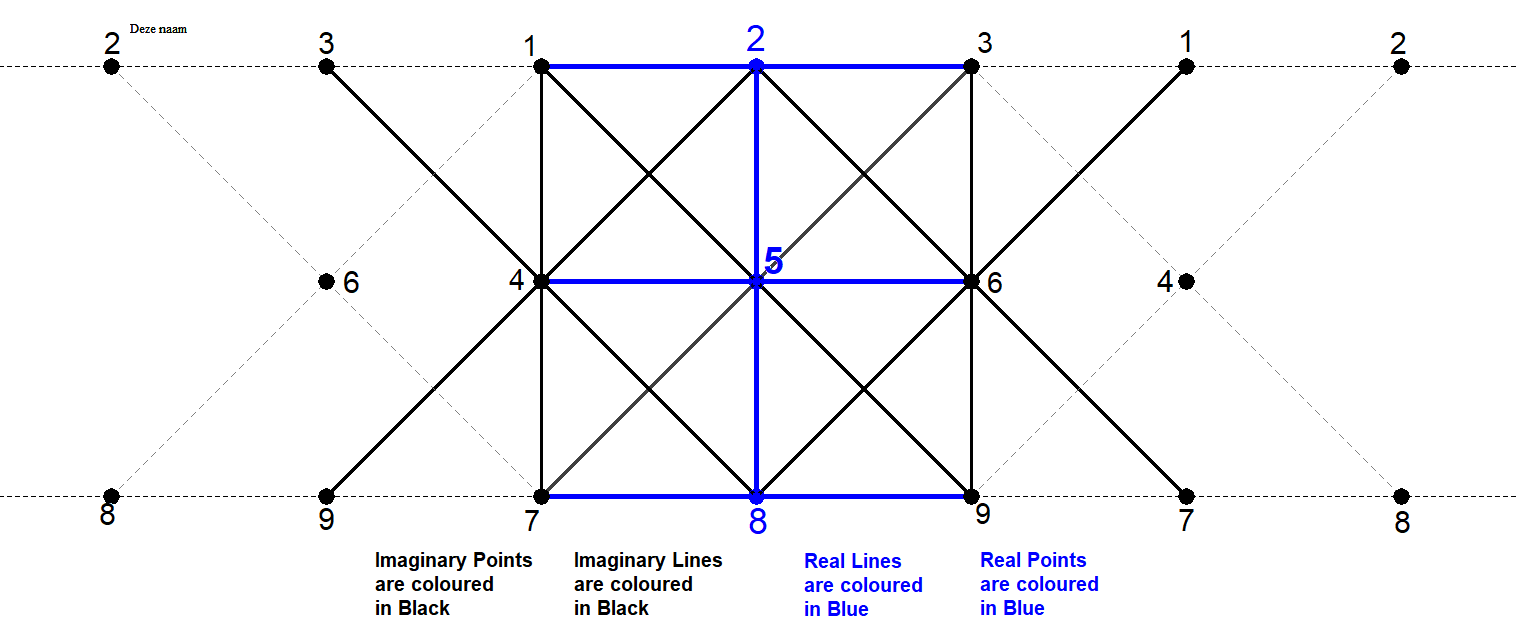
The 9 Flexpoints (3 real and 6 imaginary) lie mutually in a strict order on 12 Flexlines (4 real and 8 imaginary).

If P and Q are flexpoints, then R = P·Q is another flexpoint. See [FL], page 137.

Since the flexpoints are points on CU and since any line always cuts a cubic in three points, there will be no more than 3 collinear flexpoints on a line segment.

This is valid for each flexpoint and therefore flexpoints occur all the time in combinations of three. When P occurs in combination with Q and R, then P and Q cannot occur with another point than R. Therefore P combines with the other 8 flexpoints in 4 pairs and so in the scheme below you will see that each knot has 4 line segments passing.

All in all, there is a limited number of 12 combinations of flexlines.

CU-12L1 Flexlines-scheme 03.fig

The flexpoints can be imagined lying on a cylindrical shape that has been cut open, allowing points to reappear on the left and right. This makes it clear how the 3-point-line-segments extend in a regular way.

In the picture above the 12 combinations are shown schematically.

For more information see [75] and [79], page 17.

There is a relationship with the Harmonic Polars Network. See CU-12P1 and QPG#2410.

Real and Imaginary Flexlines

Of the 12 Flexlines, there are always 4 real and 8 imaginary ones for all cubics.

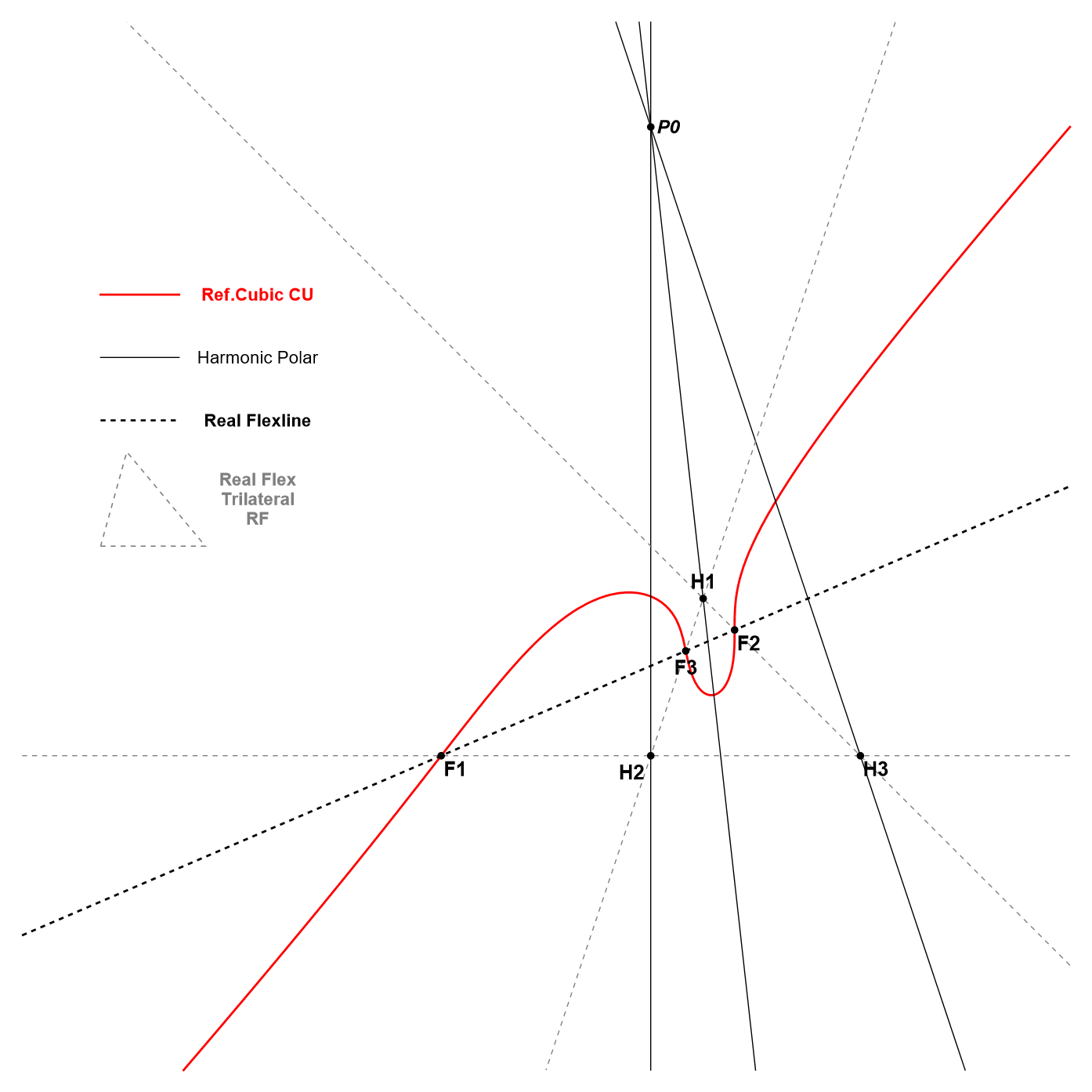
The 4 real Flexlines are:

• The main real Flexline. The standard method for determining the flexpoints involves drawing the Hessian of CU. Refer to CU-Cu1 for details. The Hessian is also a cubic, meaning that the Reference Cubic CU and its Hessian intersect at nine points. These points constitute the nine flex points, of which only three are real and collinear, thereby constituting the main real flexline.
• The triplet of real Flexlines (each passing through one real Flexpoint), also described as the real Flexline Trilateral. Eckart Schmidt discovered their construction, as outlined in QPG#2635 for the bipartite cubic and in QPG#2747 for the general cubic.

CU-HE-12L1abc-32-bipartite cubic.png

Estimated human page views: 9