CU-5  Normal form of a cubic equation

General form of a cubic equation

A cubic equation in barycentric coordinates can be expressed in general form as:

c₁ x³ + c₂ y³ + c₃ z³ + c₄ x² y + c₅ x² z + c₆ x y² + c₇ y² z + c₈ x z² + c₉ y z² + c₀ x y z = 0

where the coordinates refer to a reference triangle ABC with vertices (1 : 0 : 0), (0 : 1 : 0) and (0 : 0 : 1).

Simplification of the cubic equation

The following simplification of a cubic equation is based on the theory of Hesse’s Form and was further developed in a discussion within the QPG Group in 2024/2025 (see [66]), where Bernard Keizer was the initiator and driving force behind the problem, contributing the majority of input.

When a reference triangle is chosen, the corresponding reference points play a pivotal role. Each target point is defined by coordinates relative to these reference points. To express the same target point in relation to a second reference triangle, a point reference transformation is required. This transformation pTf can be formulated as follows.

Let target point X(x,y,z) be identified with respect to a reference triangle with vertices (1 : 0 : 0), (0 : 1 : 0) and (0 : 0 : 1). Let triangle P1(p1x : p1y : p1z), P2(p2x : p2y : p2z), P3(p3x : p3y : p3z) be the second reference triangle. Then the new coordinates of X with respect to triangle P1P2P3 will be defined by:

pTf (P1, P2, P3, X) =

(Det[(X, P2, P3)] (p1x+p1y+p1z),

Det[(P1, X, P3)] (p2x+p2y+p2z),

Det[(P1, P2, X)] (p2x+p2y+p2z)),

where Det is the determinant of the 3×3-matrix formed by the 3 sets of point coordinates indicated.

The point reference transformation applied for all points (x,y,z) on CU from reference triangle (1 : 0 : 0), (0 : 1 : 0) and (0 : 0 : 1) to reference triangle P1,P2,P3 will use pTf^-1 for alle points on CU.

Let H1H2H3 be the real flex triangle H₁H₂H₃ of the reference cubic. This is the triangle bounded by the 3 real flexlines, each passing through one of the 3 real flexpoints.

First normal form of a cubic equation

When the reference triangle is changed to this flex triangle, the equation of the cubic simplifies to a form, here called the first normal form:

• b₁ x³ + b₂ y³ + b₃ z³ + b₀ x y z = 0.

In order to connect to later developments the first normal form is rearranged to:

• a₁³ x³ + a₂³ y³ + a₃³ z³ + k a₁ a₂ a₃ x y z = 0

So when we work with the real flex triangle H₁H₂H₃ as reference triangle then there are coefficients (a₁, a₂, a₃, k) such that:

• CU = a₁³ x³ + a₂³ y³ + a₃³ z³ + k a₁ a₂ a₃ x y z = 0

Second normal form of a cubic equation

Another transformation can be applied mapping (a₁ x) x, (a₂ y) y, (a₃ z) z, resulting in the second normal form:

• x³ + y³ + z³ + k x y z = 0

This form is known as Hesse’s Form.

Thus, after performing two transformations, the equation of a cubic in its general form is transformed (projectively equivalent) into Hesse’s form.

For a proof of the existence of a projectively equivalent mapping from any smooth cubic in general form to Hesse’s form see [75], page 4 and [76], page 2.

Flexpoints, Flexlines and Harmonic Polars in first normal form

After the projective transformation next coordinates/equations follow from consequent calculations.

The 9 flexpoints are

• F₁ = (0, -a₃, a₂)          real point
• F₂ = (-a₃, 0, a₁)          real point
• F₃ = (-a₂, a₁, 0)          real point
• F₄ = (0, -i₂ a₃, a₂)      imaginary point
• F₅ = (0, -i₁ a₃, a₂)      imaginary point
• F₆ = (-i₂ a₃, 0, a₁)      imaginary point
• F₇ = (-i₁ a₃, 0, a₁)      imaginary point
• F₈ = (-i₂ a₂, a₁, 0)      imaginary point
• F₉ = (-i₁ a₂, a₁, 0)      imaginary point

where i1 and i2 are the primitive cube roots of unity: i₁ = (-1)^2/3 and i₂ = -(-1)^1/3. See Note-1.

The coordinates of all flexpoints show that they all lie on one of the sidelines of the reference triangle.

The 12 Flexlines are:

• L₁₂₃ = (a₁, a₂, a₃)            real Flexline F₁F₂F₃: a₁ x + a₂ y + a₃ z = 0
• L₁₄₅ = (1, 0, 0)                 real Flexline F₁F₄F₅: x = 0
• L₂₆₇ = (0, 1, 0)                 real Flexline F₂F₆F₈: y = 0
• L₃₈₉ = (0, 0, 1)                 real Flexline F₃F₇F₉: z = 0
• L₁₇₉ = (i₂ a₁, a₂, a₃)        imaginary Flexline F₁F₇F₉
• L₁₆₈ = (i₁ a₁, a₂, a₃)        imaginary Flexline F₁F₆F₈
• L₂₅₈ = (a₁, i₂ a₂, a₃)        imaginary Flexline F₂F₅F₈
• L₂₄₉ = (a₁, i₁ a₂, a₃)        imaginary Flexline F₂F₄F₉
• L₃₄₆ = (a₁, a₂, i₂ a₃)        imaginary Flexline F₃F₄F₆
• L₃₅₇ = (a₁, a₂, i₁ a₃)        imaginary Flexline F₃F₅F₇
• L₄₇₈ = (a₁, i₁ a₂, i₁ a₃)    imaginary Flexline F₄F₇F₈
• L₅₆₉ = (a₁, i₂ a₂, i₂ a₃)    imaginary Flexline F₅F₆F₉

where i1 and i2 are the primitive cube roots of unity: i₁ = (-1)^2/3 and i₂ = -(-1)^1/3. See Note-1.

Note that after the projective transformation indeed the triangle bounded by L₁₄₅, L₂₆₇, L₃₈₉ is the new reference triangle with sidelines (1,0,0), (0,1,0), (0,0,1), and consequently with vertices H1(1,0,0), H2(0,1,0), H3(0,0,1) of the new reference triangle.

The 9 Harmonic Polars are:

• L₁ = (0, a₂, -a₃)          real line
• L₂ = (a₁, 0, -a₃)          real line
• L₃ = (a₁, -a₂, 0)          real line
• L₄ = (0, a₂, -i₂ a₃)      imaginary line
• L₅ = (0, a₂, -i₁ a₃)      imaginary line
• L₆ = (a₁, 0, -i₂ a₃)      imaginary line
• L₇ = (a₁, 0, -i₁ a₃)      imaginary line
• L₈ = (a₁, -i₂ a₂, 0)      imaginary line
• L₉ = (a₁, -i₁ a₂, 0)      imaginary line

where i1 and i2 are the primitive cube roots of unity: i₁ = (-1)^2/3 and i₂ = -(-1)^1/3. See Note-1.

Harmonic Polar-Crosspoint P0

The 3 real Harmonic Polars are concurrent in P0 (1/a₁, 1/a₂, 1/a₃).

P0 is the trilinear pole wrt the reference triangle H₁H₂H₃. of the real Flexline F₁F₂F₃: L₁₂₃.

Conversely L₁₂₃ is the trilinear polar of P0 wrt the reference triangle H₁H₂H₃.

The Hessian of CU

We know:

CU = a₁³ x³ + a₂³ y³ + a₃³ z³ + k a₁ a₂ a₃ x y z = 0

After calculation the Hessian HE of CU appears as:

HE = a₁³ x³ + a₂³ y³ + a₃³ z³ + k’ a₁ a₂ a₃ x y z = 0

where k’ = -(108 + k³) / 3

The Syzygetic Pencil

All Cubics passing through the 9 Flexpoints of CU are called cubics of the Syzygetic Pencil.

CU and its Hessian mutually intersect in the 9 Flexpoints of CU. Therefore they are called members of the Syzygetic Pencil.

The 3 sidelines of the real flex triangle H₁H₂H₃ (being the 3 real flexlines resp. through F₁, F₂, F₃) form together also a degenerate cubic, which will be called here RF. On these 3 lines all 9 Flexpoints occur. So it is also a member of the Syzygetic Pencil.

Since it is a pencil every Cubic in it can be described as t CU₁ + (1-t) CU₂, where CU₁ and CU₂ are also members of the pencil.

We now ask the question of finding a cubic FE as linear combination of CU and HE such that RF is its hessian.

Specifically we need to find CUx = Hessian of t CU + (1-t) HE.

It appears that there are 9 values of t that provide a solution.

However, upon substituting these values of t, it turns out that there are only 2 distinct solutions.

• FE = a₁³ x³ + a₂³ y³ + a₃³ z³

and

• RF = a₁ a₂ a₃ x y z.

FE is the main part and will be called here the Core Curve, RF is the degenerate part and will be called here the Residual Curve.

RF is actual the degenerate cubic consisting of the three sidelines (x=0, y=0, z=0) of the reference triangle, which are the three real Flexlines, which indeed contain the 9 Flexpoints.

Moreover FE and RF are derived from the pencil t CU + (1-t) HE and therefore both pass through the 9 Flexpoints and consequently are members of the Syzygetic Pencil.

It also appears that FE and RF share the same Hessian, namely RF.

Hessians and PreHessians

Since a Hessian is also a cubic, it is also possible to calculate the Hessian of the Hessian, and further downwards.

Moreover it is possible, knowing some cubic CU, to find out for which upper cubic CU is the Hessian. There are 3 of these cubics called the PreHessians pHE₁, pHE₂, pHE₃.

So per definition the Hessian of all three cubics pHE₁, pHE₂, pHE₃ will be CU.

So “upwards” there are 3 PreHessians of a cubic and “downwards” there is 1 Hessian per cubic.

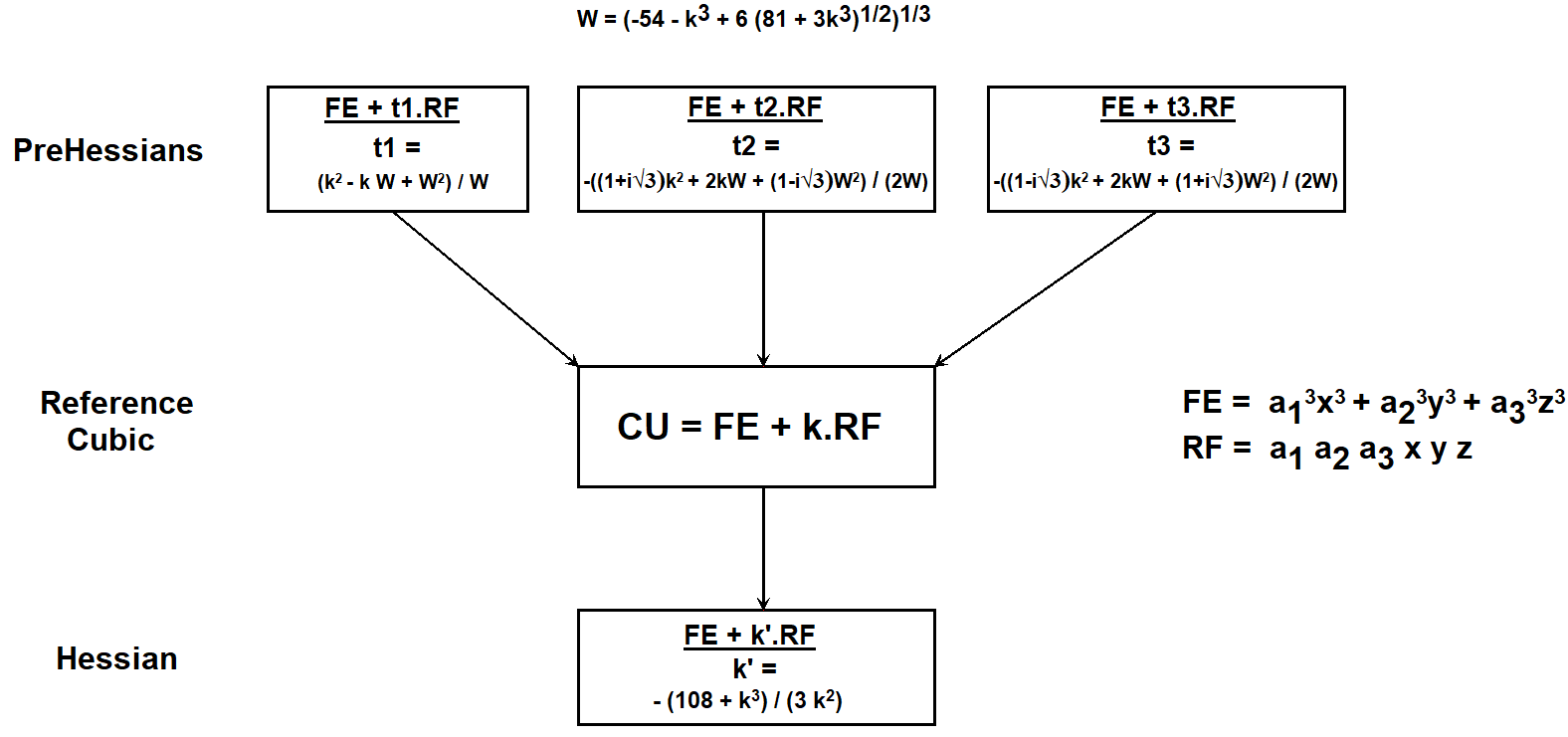
CU-3Cu1 CU-HE-pHE1-pHE2-pHE3 picture-03.fig

From the equations of t1, t2, t3 it follows that there will be three real preHessians when k <= -3. When k > -3, there will be one real preHessian and two imaginary preHessians.

Examples

The 3 PreHessians of FE are also of the form FE + k.RF. Its Hessian is RF.

The 3 PreHessians of RF are RF itself and FE (counting twice). Its Hessian is again RF.

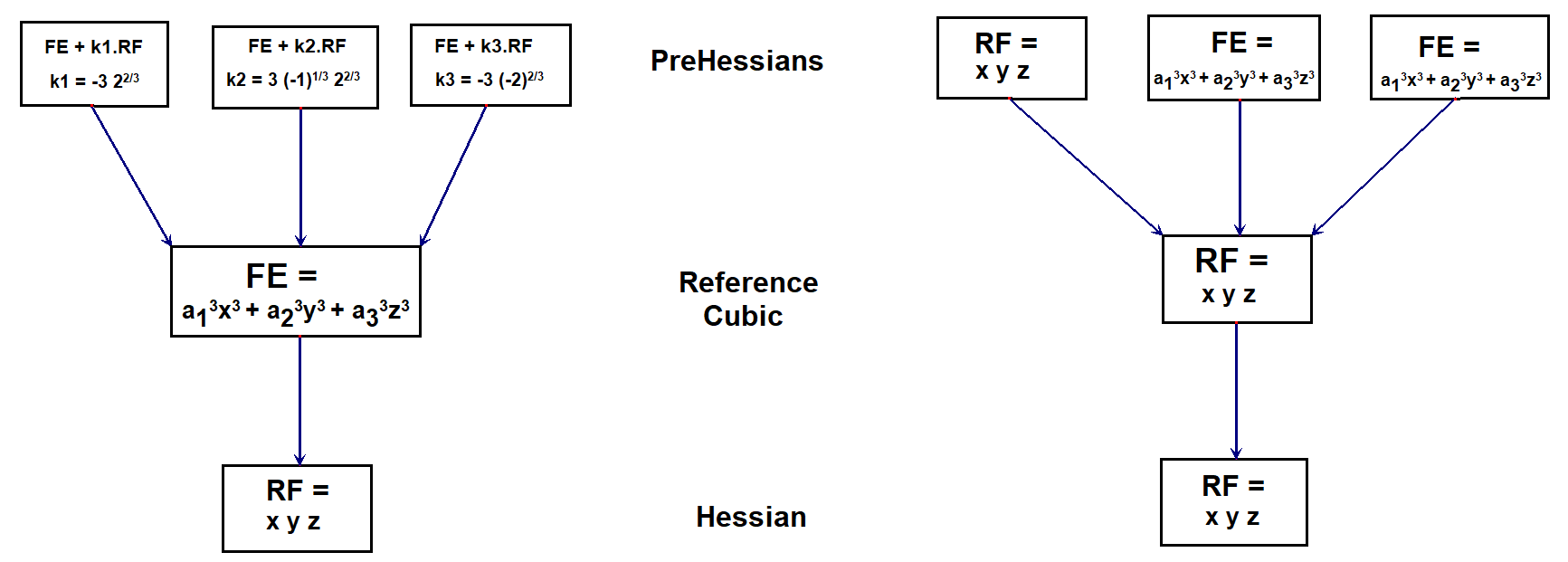
CU-3Cu1 CU-HE-pHE1-pHE2-pHE3 picture-02.fig

The Cayleyan

Let CU = a₁³ x³ + a₂³ y³ + a₃³ z³ + k a₁ a₂ a₃ x y z = 0

Numerical analyses show that the Cayleyan of CU has this expression:

CAY =

a₁⁶ x⁶ + a₂⁶ y⁶ + a₃⁶ z⁶

+ u (a₁³ a₂³ x³ y³ + a₁³ a₃³ x³ z³ + a₂³ a₃³ y³ z³)

+ v (a₁⁴ a₂ a₃ x⁴ y z + a₁ a₂⁴ a₃ x y⁴ z + a₁ a₂ a₃⁴ x y z⁴)

+ w (a₁² a₂² a₃² x² y² z²)

u, v, w are fixed expressions probably have variables a₁, a₂, a₃, and k in it.

It still isn’t clear which expressions they have.

Pictures of CU = a₁³ x³ + a₂³ y³ + a₃³ z³ + k a₁ a₂ a₃ xyz

for different values of a1, a2, a3, k

different cubics as a1 varies 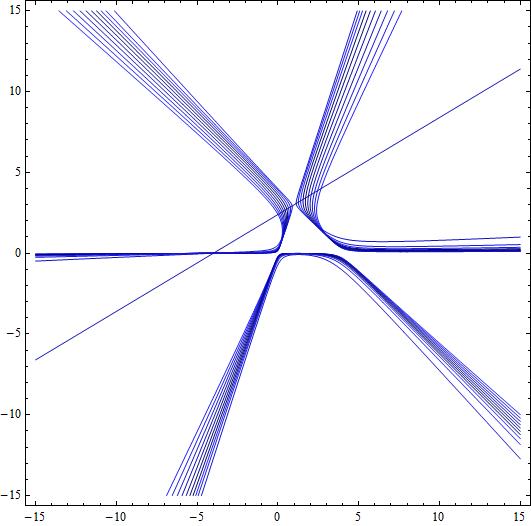CU-a1is-10-to-0 a2is-2 a3is-4 kis100.jpg a1 = -10 → 0, a2 = -2, a3 = -4, k = 100 when a1=0 the cubic degenerates in 3 lines, one of which is a real flexline	different cubics as a2 varies 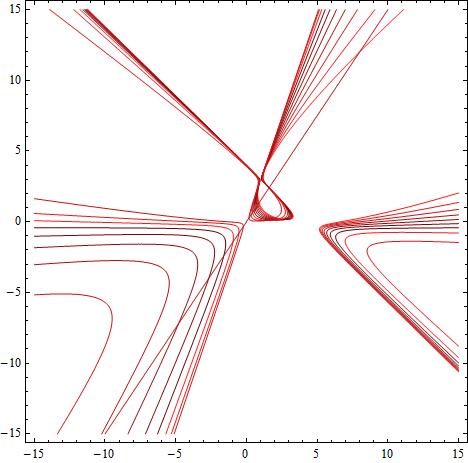CU-a1is1 a2is-10-to-0 a3is-4 kis100.jpg a1 = 1, a2 = -10 → 0, a3 = -4, k = 100 when a2=0 the cubic degenerates in 3 lines, one of which is a real flexline
different cubics as a3 varies 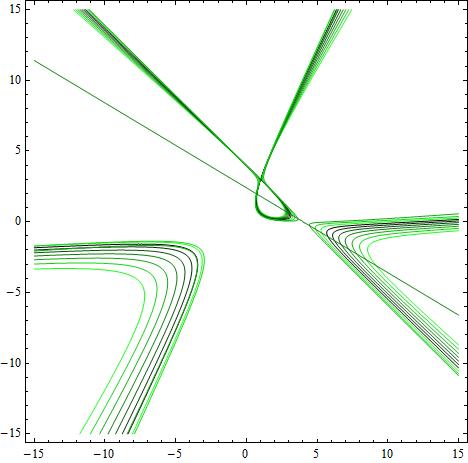CU-a1is1 a2is-2 a3is-10-to-0 kis100.jpg a1 = 1, a2 = -2, a3 = -10 → 0, k = 100 when a1=0 the cubic degenerates in 3 lines, one of which is a real flexline	different cubics as ai varies with k=-3 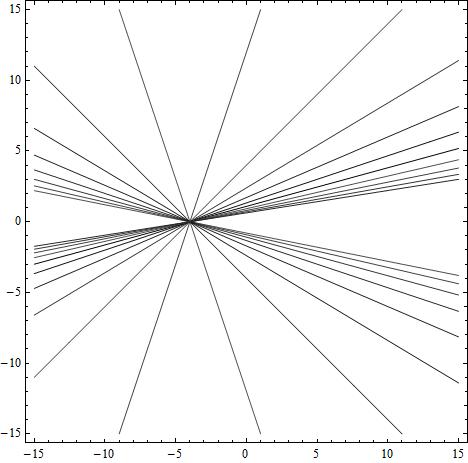CU-a1is-10-to-0 a2is-2 a3is-4 kis-3.jpg a1 = -10 → 7, a2 = -2, a3 = -4, k = -3 all cubics degenerate in lines when k = -3 for all values of (a1,a2,a3)

different cubics as variable k varies

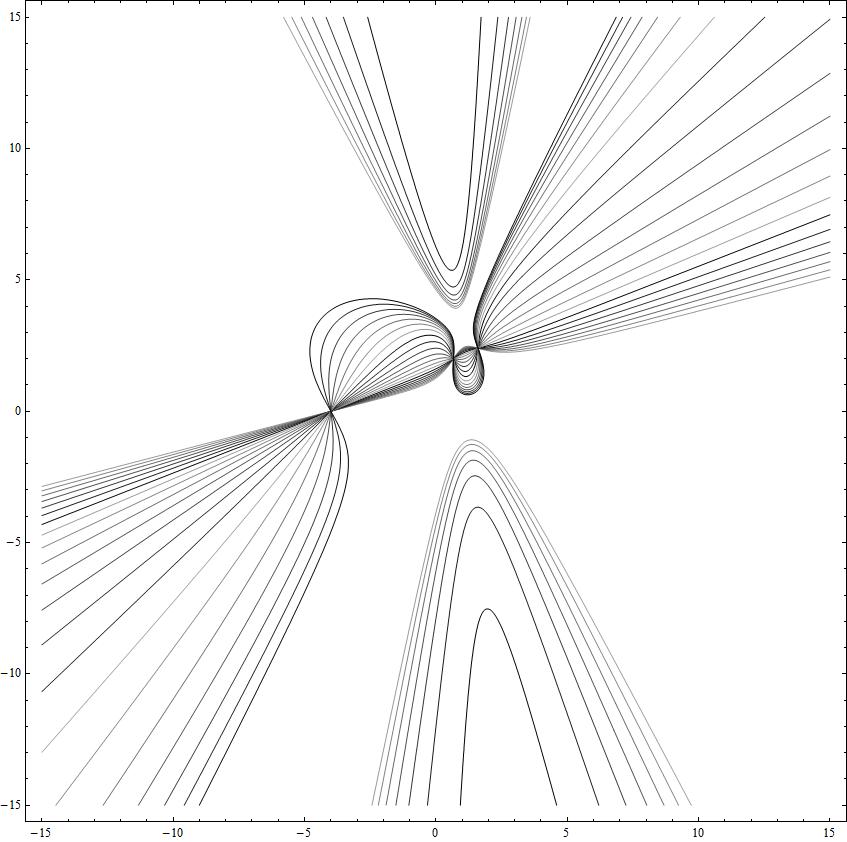
CU-a1is1 a2is-2 a3is-4 kis-10to10.jpg

a1 = 1, a2 = -2, a3 = -10 -> 0, k = -10 -> 10

all cubics pass through the 3 real Flexpoints

when k = -3 the cubic degenerates in a real line and an (imaginary) conic

Picture of CU / HE / CAY

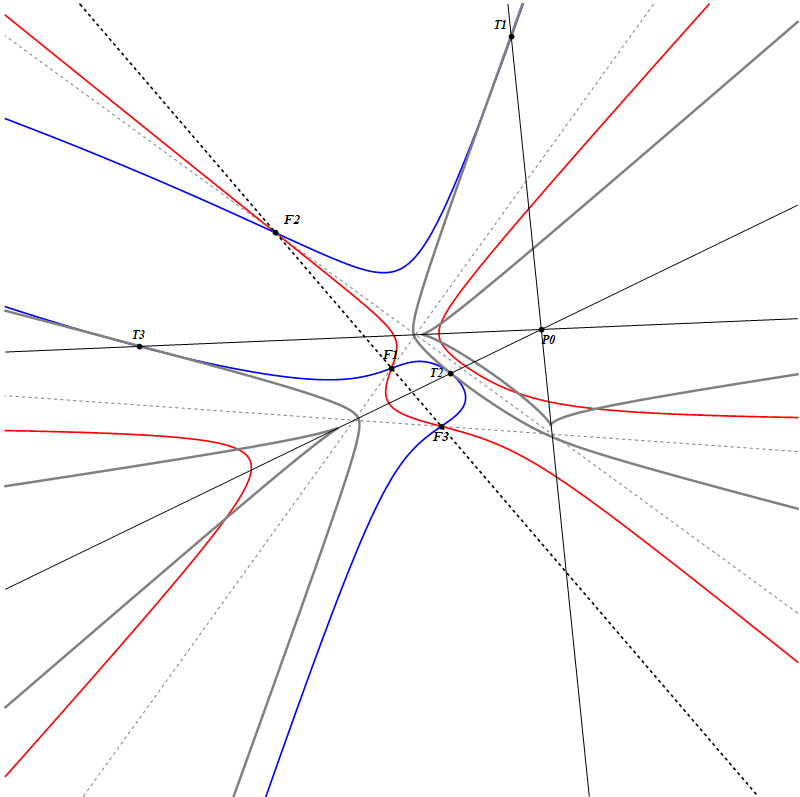
9P-s-Cu1” target=”_blank”>9P-s-Cu1 Hessian-plus Flexlines-41-FE-kRF-example.nb

Reference Cubic CU is red

Hessian HE is blue

Cayleyan CAY is gray

F1, F2, F3 are the real Flexpoints

The 1 gray dotted line is the real Flexline F1F2F3

The 3 light gray dotted lines are the real Flexlines

The 3 black lines are the 3 Fi-Harmonic Polars

T1, T2, T3 are intersection points of corresponding Fi-Tangent and Fi-Harmonic Polar

P0 is the common intersection point of the 3 real Fi-Harmonic Polars

Picture-1 of CU / HE / FE / RF / CAY

9P-s-Cu1” target=”_blank”>9P-s-Cu1 Hessian-plus Flexlines-54-Normalized-Cayleyan.nb

Picture-2 of CU / HE / FE / RF / CAY

9P-s-Cu1” target=”_blank”>9P-s-Cu1 Hessian-plus Flexlines-55-Normalized-Cayleyan.nb

Picture of CU / HE / pHE1, pHE2, pHe3 (preHessians)

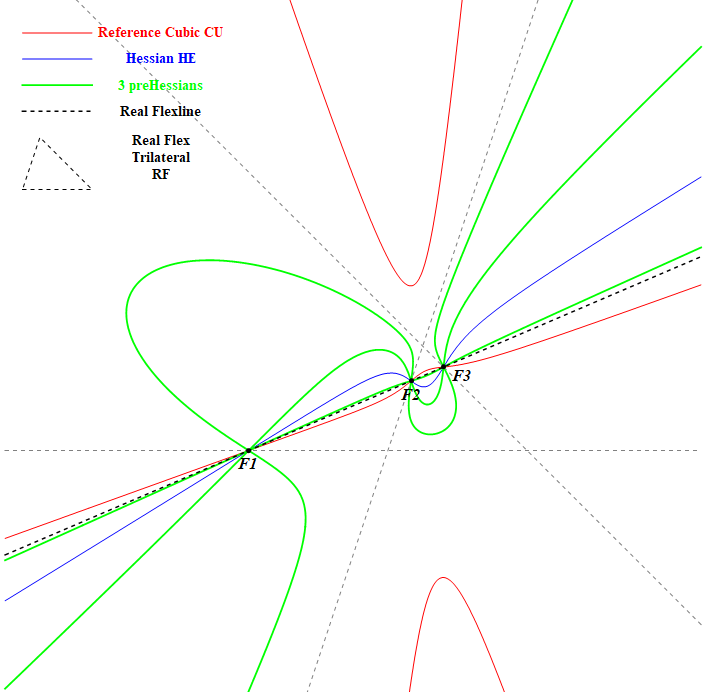
CU-HE-pHE-01.nb

Note 1.

A “primitive cube root of unity” or “primitive third root of 1” is a complex number that, when raised to the power of 3,

equals 1, and it is not equal to 1 itself.

There are exactly three cube roots of unity:

1.  1
2.  i1 = -1/2 + (i √3) / 2
3.  i2 = i1² = -1/2 – (i √3) / 2

Among these, i1 and i2=i1² are called primitive cube roots of unity because they generate all cube roots of unity when raised to successive powers, and they themselves are not equal to 1.

The primitive cube roots of unity have the following properties:

– i1³ = 1

– i1 <> 1 and i2 <>1

– 1 + i1 + i2 = 0

Geometrically, they are the points on the complex plane that form the vertices of an equilateral triangle inscribed in the unit circle, with one vertex at 1.

Estimated human page views: 17