CU-IP-3P1 Set of 3 Quasi-Miquel Triangles

Each cubic has 3 special inscribed triangles. They are called the Quasi-Miquel Triangles, because they are related to the Miquel Triangle (QA-Tr2) in a Quadrangle.

Their locations are fixed on the cubic. Every cubic has its own fixed set of 3 Quasi-Miquel Triangles.

However not every vertex of these triangles is always real. There can be imaginary vertices depending on the shape of the cubic.

In principle, every asymptote of the cubic has such a related triangle.

When the reference cubic has only one real asymptote, then there will be one such triangle of which at least one vertex will be real.

When the reference cubic has three real asymptote, then there will be three such triangles of which per asymptote at least one vertex will be real.

So it can be said that each cubic has three of these triangles with a total of 3×3 vertices, but in the minimum case only one vertex will be real and in the maximum case there will be 3×3 vertices real.

It’s all depending on the shape of the cubic.

From here the different options will be discussed.

The Quasi-Miquel Triangles are actually the Diagonal Triangles of the three Quadrangles formed by the sets of 4 Anallagmatic Points (CU-IP-4P1) that can be constructed per CU-asymptote.

Also within the sets of 4 Anallagmatic Points (CU-IP-4P1) not always all points will be real.

There are these situations:

1. When the reference cubic has only one real asymptote, then there will be 2 or 4 real Anallagmatic points.
   • When there are 2 real Anallagmatic points P1 and P2, then there will be one real vertex of the corresponding Quasi-Miquel Triangle. It is the 3^rd intersection point of P1P2 with CU.
   • When there are 4 real Anallagmatic points P1, P2, P3 and P4, then there will be 3 real vertices of the corresponding Quasi-Miquel Triangle. They are the vertices of the Diagonal Triangle (QA-Tr1) of the Quadrangles formed by (P1,P2,P3,P4).
2. When three asymptotes are real, then there will be 2 or 4 real anallagmatic points per asymptote. Again the same rules 1a and 1b apply for each asymptote.

Pictures of QMT’s on different types of Cubics

Picture Anallagmatic Points and Quasi-Miquel Point on a Monopartite Cubic

There is 1 real asymptote and there are 2 real Anallagmatic Points P1 and P2 and 1 real Quasi-Miquel-Point M (the only real vertex of a Quasi-Miquel Triangle).

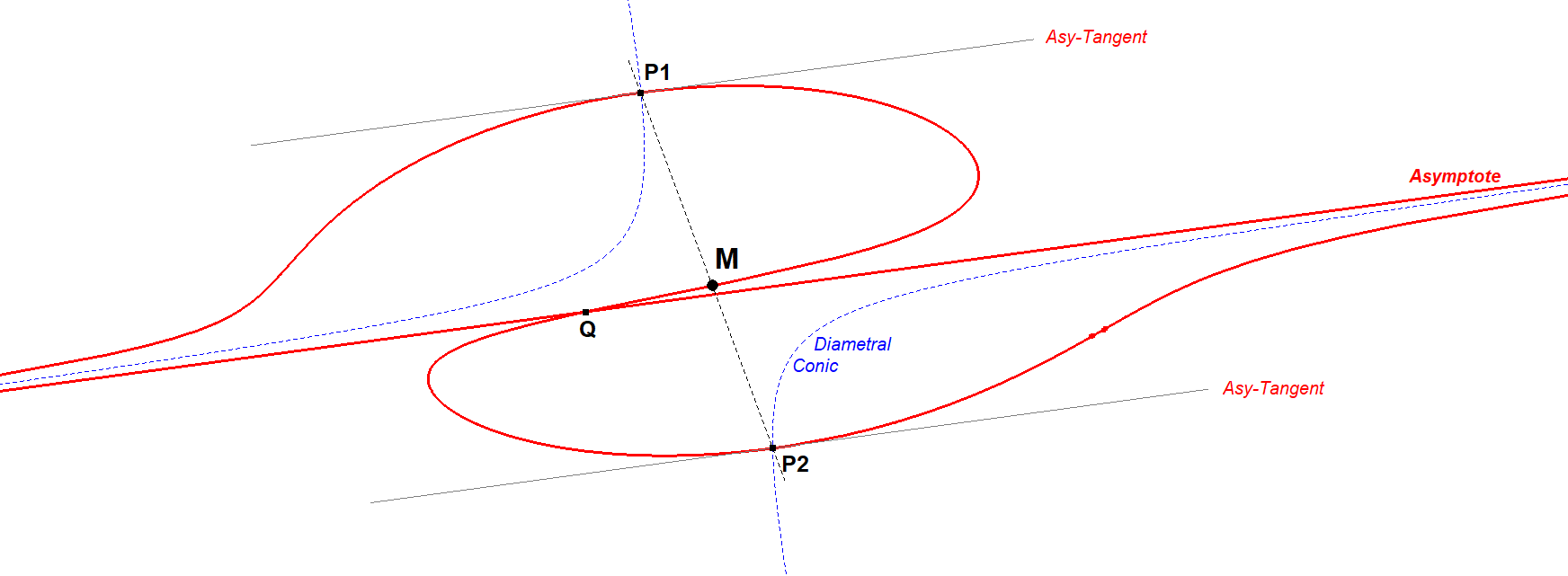
CU1-Monopartite Cubic-05-Anal-Miq-Point.fig

Picture Anallagmatic Points and Quasi-Miquel Triangle on a Bipartite Cubic

There is 1 real asymptote and there are 4 real Anallagmatic Points and a Quasi-Miquel-Triangle with 3 real vertices.

CU2-Bipartite Cubic-21-Anall-Miquel-Points.fig

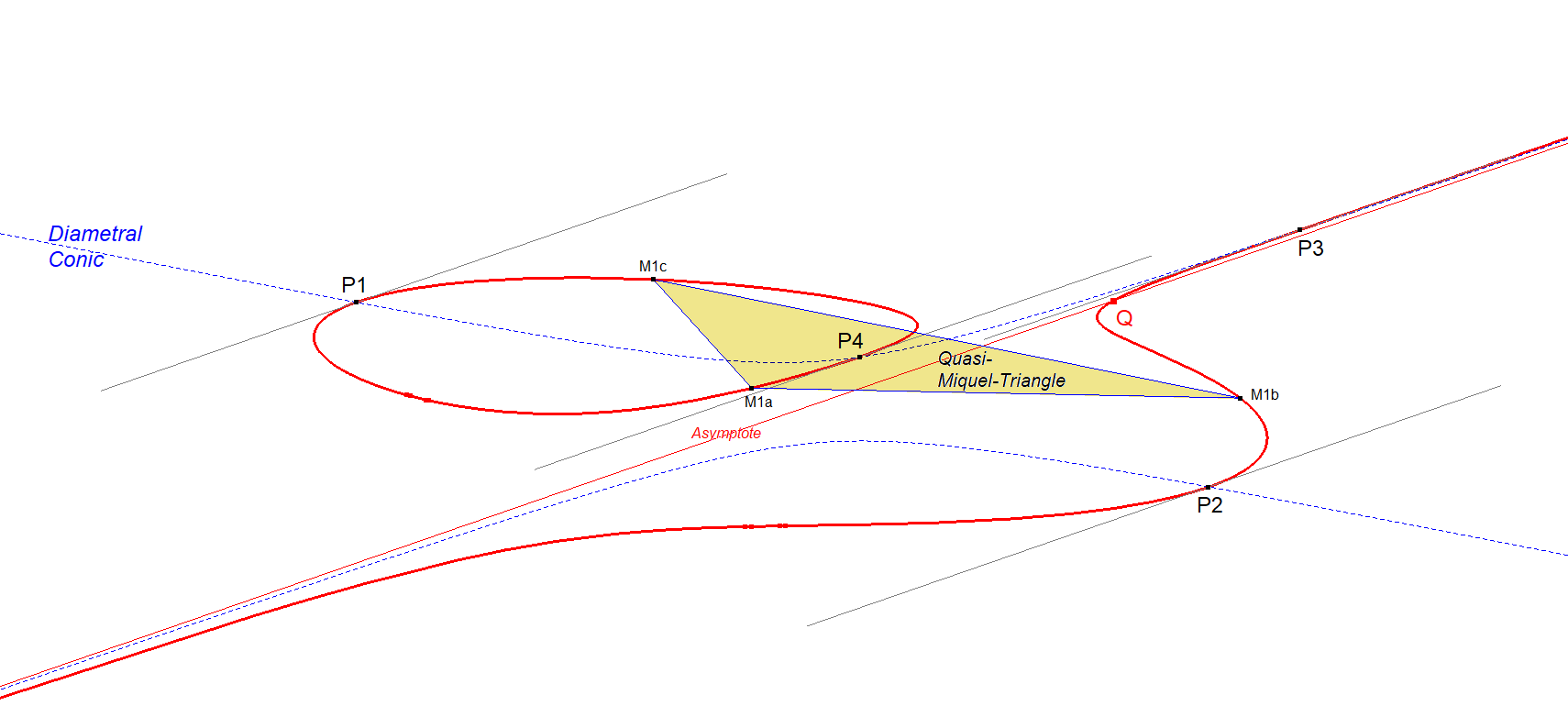
Picture Anallagmatic Points and Quasi-Miquel Triangle on a Tripartite Cubic

There are 3 real asymptotes witch each 2 real Anallagmatic Points (P1a,P1b, P2a,P2b, P3a,P3b) and each 1 Quasi-Miquel-Triangle with each 1 real vertex (M1, M2, M3).

CU3-Tripartite Cubic-50-DiametralConics-Anall-Miq-Points.png

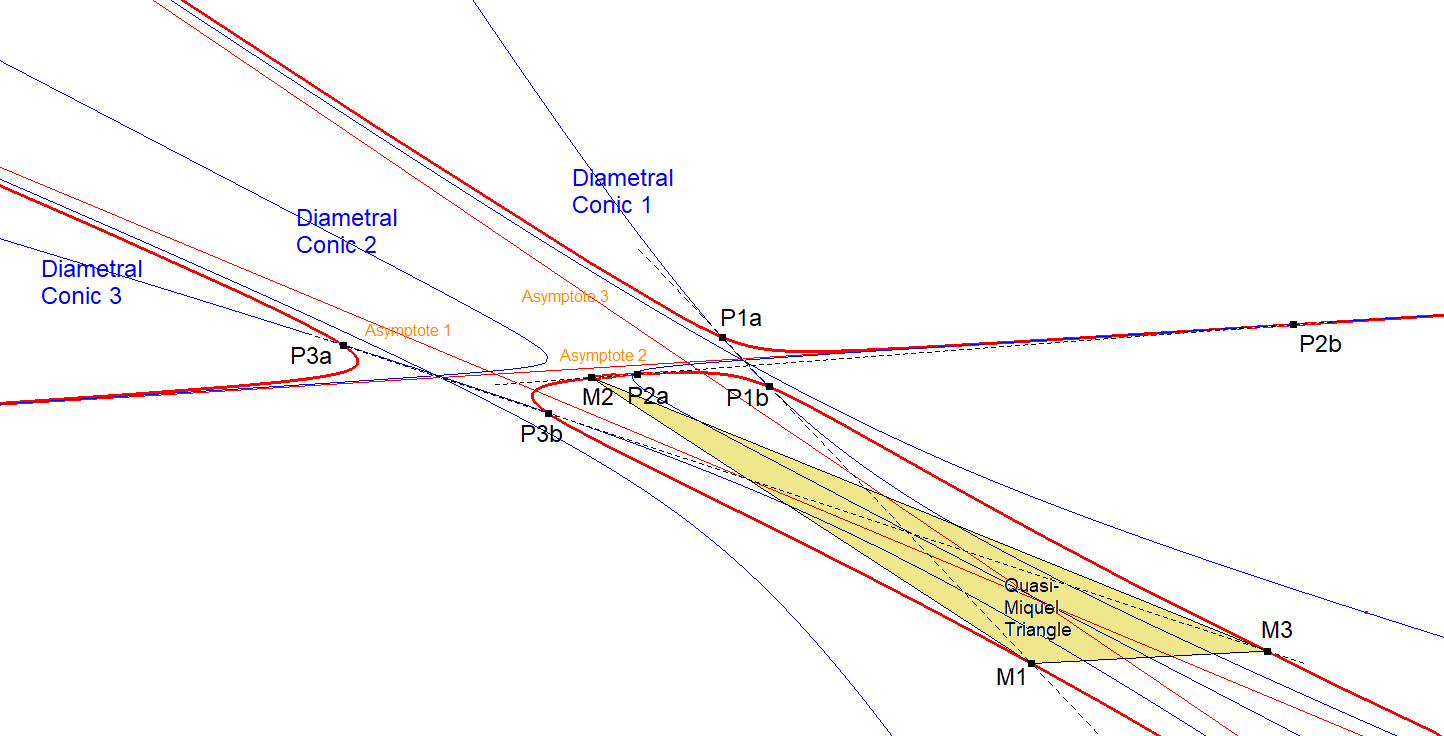
Picture Anallagmatic Points and Quasi-Miquel Triangle on a Bipartite Cubic

Now there are 3 Quasi-Miquel Triangles.

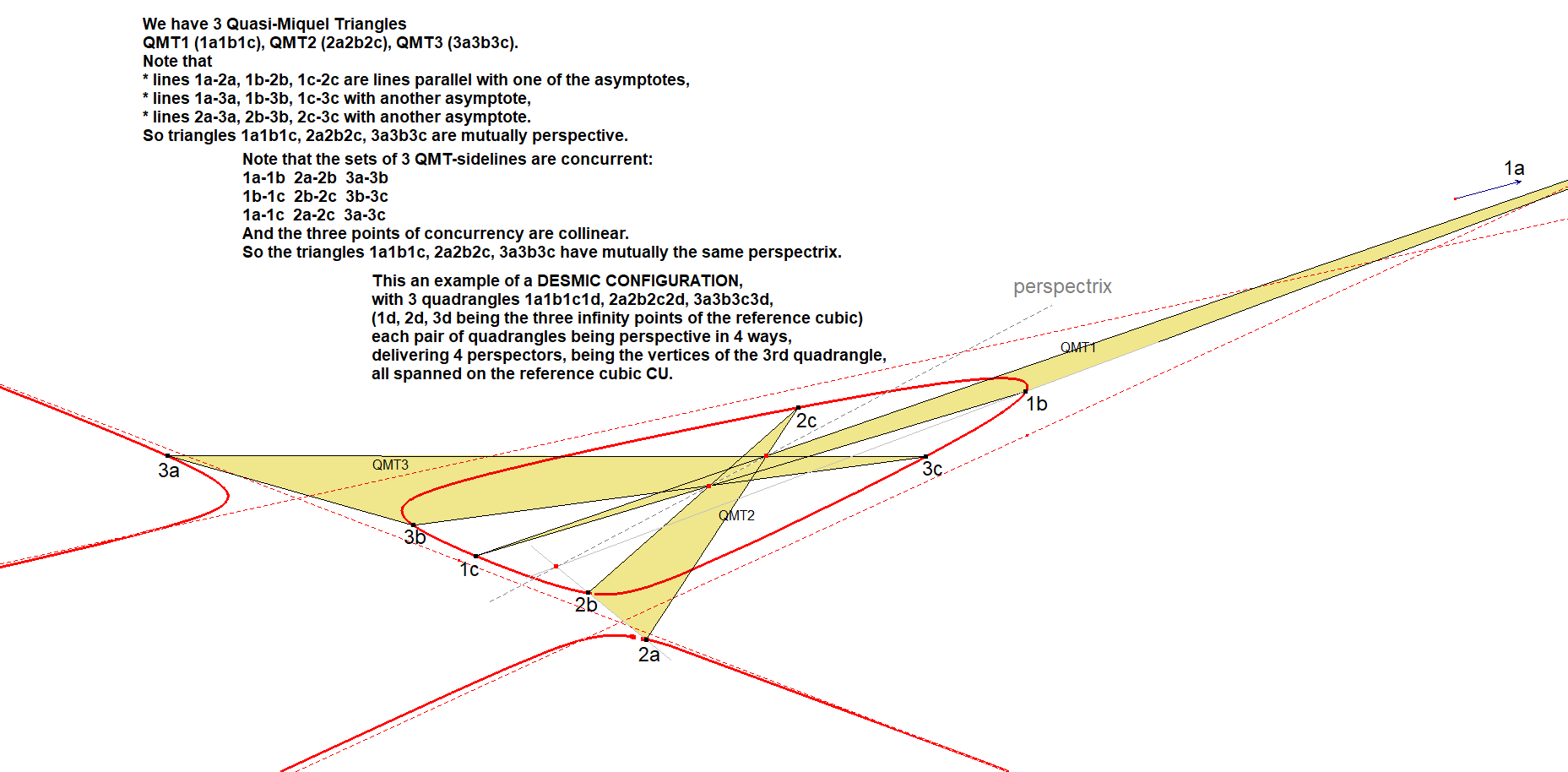
Special property:

The set of 3 Quasi-Miquel Triangles in combination with the CU-infinity points form a Desmic Configuration.

See QPG#2263. See also EQF/QA-Tr-1.

CU4-Quadripartite Cubic-with Diametral Conics-08-plus QMTs.fig

Note:

The 4^th branch of the Quadripartite Cubic is not visible at this picture.

It passes at the left through the utmost vertex of QMT1.

QUASI-MIQUEL TRIANGLE ON A CIRCULAR CUBIC

On the Circular Cubic there are additional special features with respect to the Quasi-Miquel Triangle.

1. Given a Bipartite Circular Cubic CUc2.

2. CUc2 has a Focus F (CU-IP-Q1a) and an asymptote intersecting CUc2 in Q.

3. The circle with Diameter QF intersects CUc2 in 4 points: Q, M1, M2, M3. Q is the intersection point of CUc2 with its asymptote and M1, M2, M3 are the vertices of the Quasi-Miquel Triangle for a Circular Cubic.

4. The internal and external bisectors of the Miquel Triangle intersect in the incenter I and excenters E1, E2, E3 of the Miquel Triangle.

5. The tangents at I, E1, E2, E3 are lines parallel to the CUc2-asymptote.

6. Therefore points I, E1, E2, E3 are the Anallagmatic Points (CU-IP-4P1) of CUc2.

7. I, E1, E2, E3 lie all on the IP-Polar Conic of CUc2 (IP=Infinity Point of CUc2), which is the Orthogonal Hyperbola, described by Eckart Schmidt in QPG#837/#1538. This allows for an easy construction of this Orthogonal Hyperbola. It is also called the Diametral Conic (CU-IP-Co1) for the Circular Cubic.

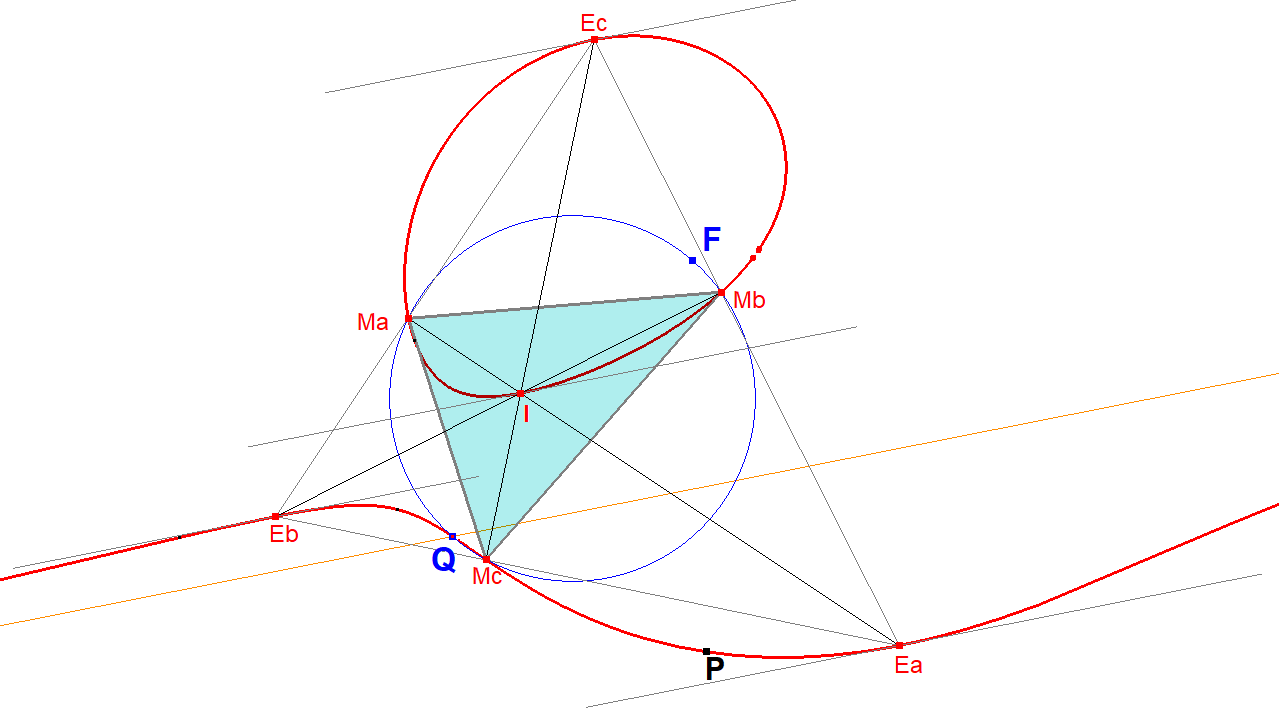
CUc2-4P In- and Excenters Miquel Triangle-01a.fig

Another construction of the Quasi-Miquel Triangle on a Circular Cubic

The monopartite case

• Given a random point P on Monopartite Cubic CUc1.
• Let T1 and T2 be the contact points of the tangents from P to the monopartite CUc1.
• Let S3 be the 3rd intersection point of T1T2 intersecting CUc1.
• Then draw a line through P intersecting CUc1 in Q1 and Q2.
• Let R1 be the 3rd intersection point of Q1S3 with CUc1.
• Let R2 be the 3rd intersection point of Q2S3 with CUc1.
• R1R2 will be a line through P.
• The Miquel point of the Quadrilateral with defining lines Q1Q2, R1R2, Q1R1, Q2R2 will be a point on CUc1. It is a fixed point independent of P and other points.

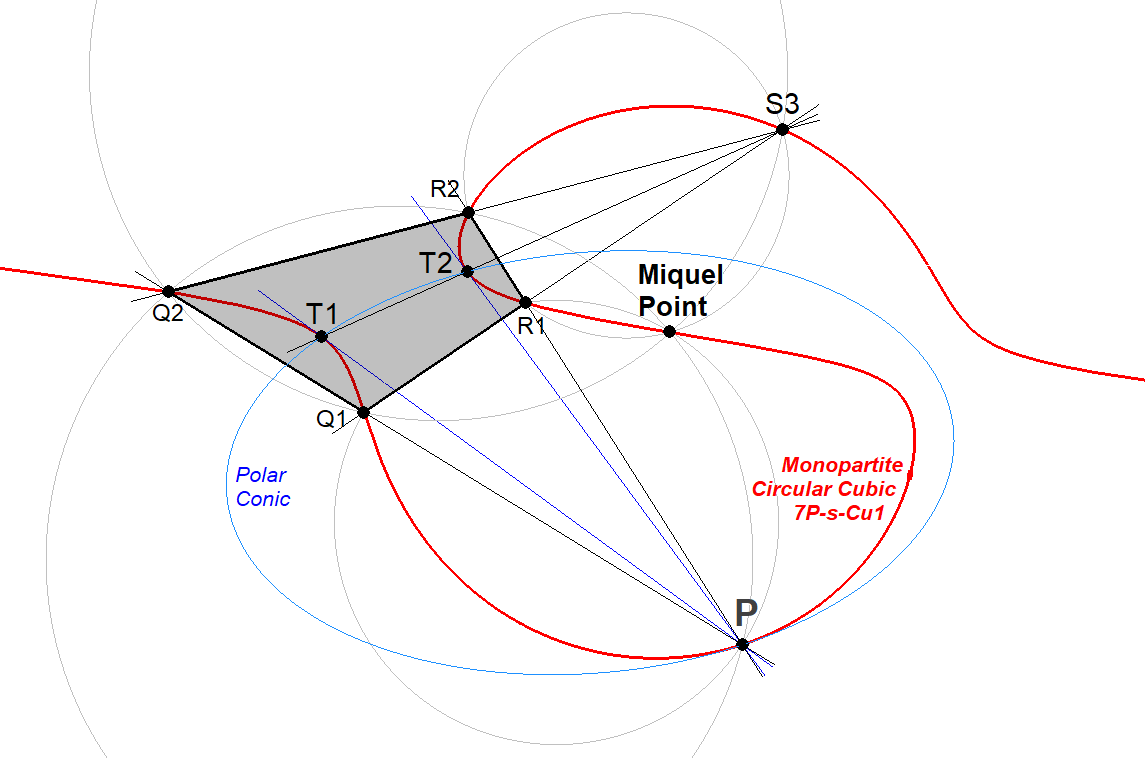
Note: The Miquel Point of a Quadrilateral (QL-P1 in EQF) is the common point of the circumcircles of each triangle formed by 3 out of 4 lines of the Quadrilateral.

The bipartite case

• Given a random point P on Bipartite Cubic CUc2.
• When CUc2 is bipartite then 4 tangents can be drawn from a random point P to the cubic and there will be 4 tangents t1, t2, t3, t4 with resp. contact points T1, T2, T3 and T4.
• In a similar construction each pair of tangents (t1,t2) and (t3,t4) deliver a Miquel Point, which appear to be identical, which is point Ma in the picture.

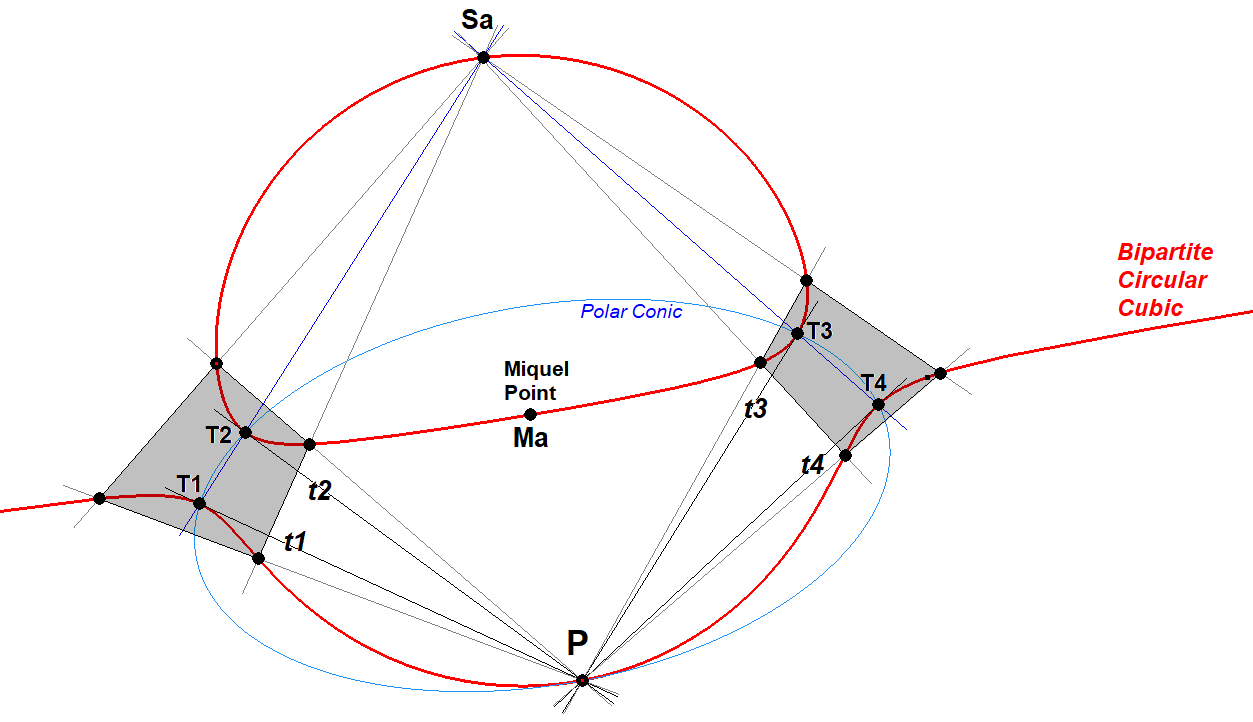
CUc2-Tr1 Miquel Triangle-02.jpg

• Likewise the pairs of tangents (t1,t3) and (t2,t4) deliver a 2^nd Miquel Point Mb and the pairs of tangents (t1,t4), (t2,t3) deliver a 3^rd Miquel point Mc. Together they form the CUc2-Miquel Triangle. It is a similar triangle as occurring in a Quadrangle, where it is called the Miquel Triangle QA-Tr1.
• In addition it appears that MaMbMc is the Miquel Triangle of the Quadrangle T1T2T3T4. Point P will be point QA-P4 of Quadrangle T1T2T3T4.

The easiest way of construction of MaMbMc in the bipartite case is by constructing the P-Polar Conic and its 4 cubic intersecting points T1, T2, T3, T4 and construct from Quadrangle T1T2T3T4 the Miquel Triangle (QA-Tr2 in EPG).

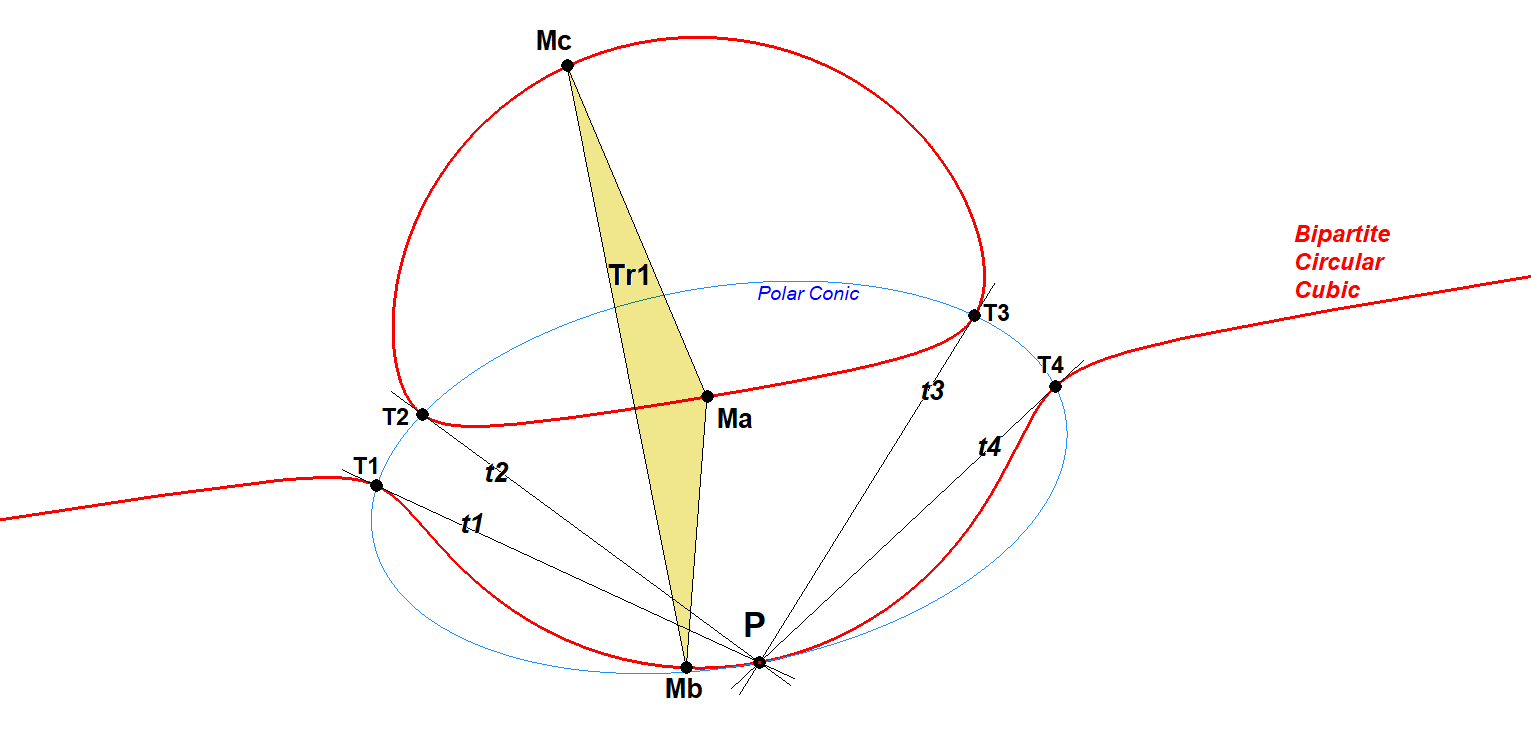
CUc2-Tr1 Miquel Triangle-01.fig

Tr1 is a triangle, unique for a bipartite circular cubic, not dependent of the choice of any point on the cubic, but only of the bipartite circular cubic itself.

Conversely Tr1 can be regarded as a reference triangle for CUc2.

In terms of Bernard Gibert’s Catalogue for Cubics in the Triangle Plane [17], the cubic is an isogonal circular pK (X(6),P) wrt Tr1, P being the pivot which lies on the infinity line and is the infinity point of the asymptote of the cubic. The Isogonal Conjugate with respect to triangle Tr1 of any cubical point P on the cubic will also lie on the cubic.

Estimated human page views: 5