← Previous Next →

CU-L-L2 L-Mean Intersect Line

Given reference cubic CU and a random line L.

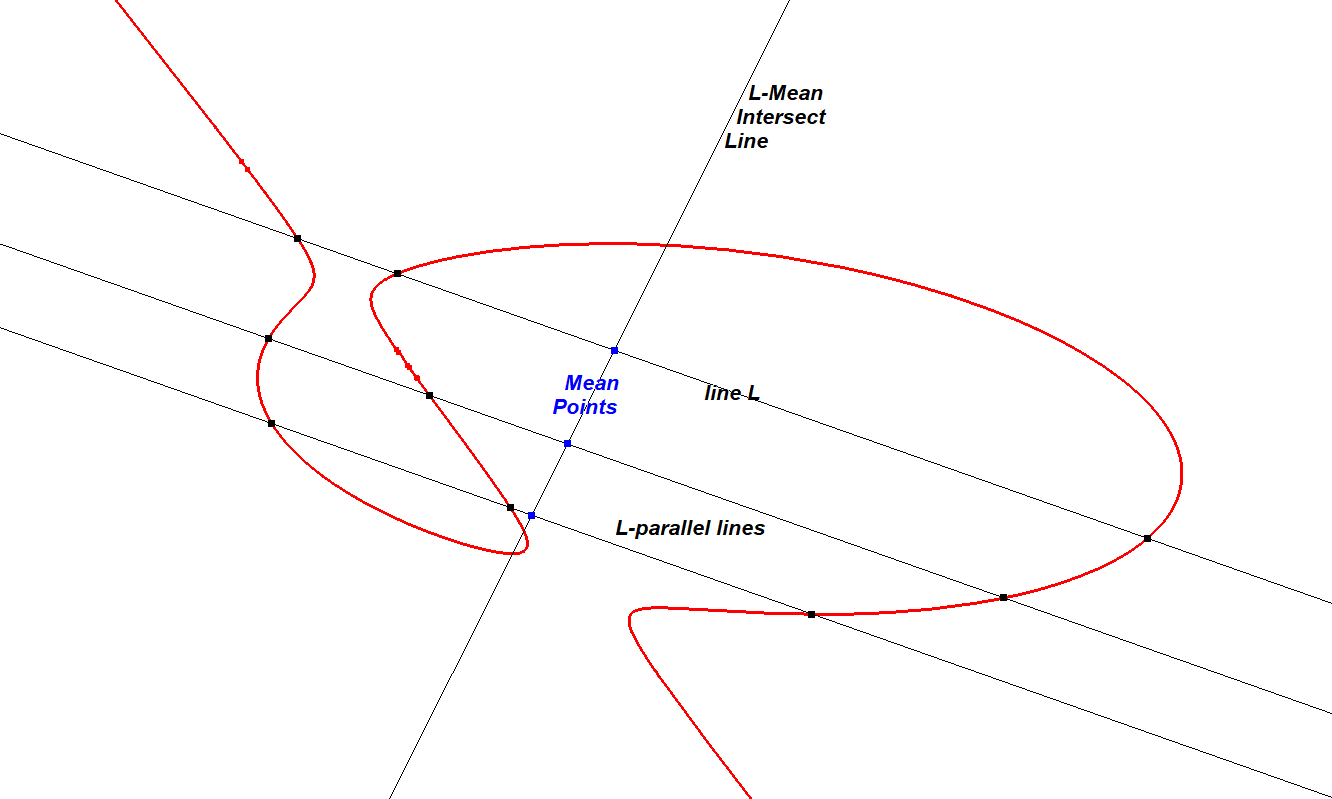
The mean point of the intersection points of CU and all L-parallel lines are collinear. See E. de Jonquiere – Mélanges de géométrie, page 197. According to him this theorem originates from Newton. It is not only valid for conics and cubics, but also for all curves of nth degree.

It is also mentioned by Cuppens at [Cuppens, page 255]. Here it is called the diameter associated to a direction d. Cuppens also mentions at page 256 that the mean point of the intersection points of L with CU coincides with the mean point of the intersection points of L with the three CU-asymptotes.

The locus of the mean point of intersection points of CU and L-parallel lines is called here the L-Mean Intersect Line CU-L-L2.

Infovisual CU-L-L2-infovisual-cvt-01.png

CU-L-L2 Mean Line of Intersection-02.fig

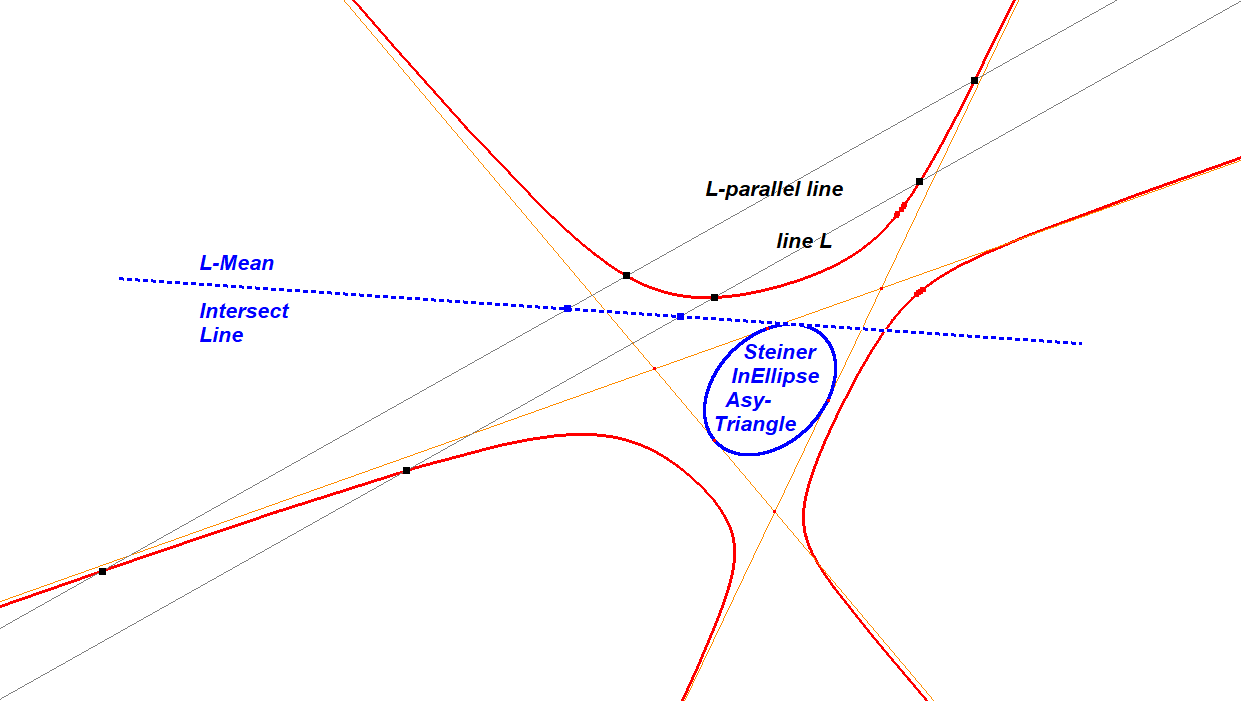
A special property of all L-Mean Intersect Lines is that they are tangent to the Steiner InEllipse of the CU-Asy-Triangle CU-Tr1. In other words, they envelop the Steiner InEllipse of the CU-Asy-Triangle. This is only visible when CU has three real asymptotes.

Infovisual CU-L-L2-infovisual-cvt-02.png

CU-L-L2 L-Mean Intersect Line-10-3-Asymptotes.fig

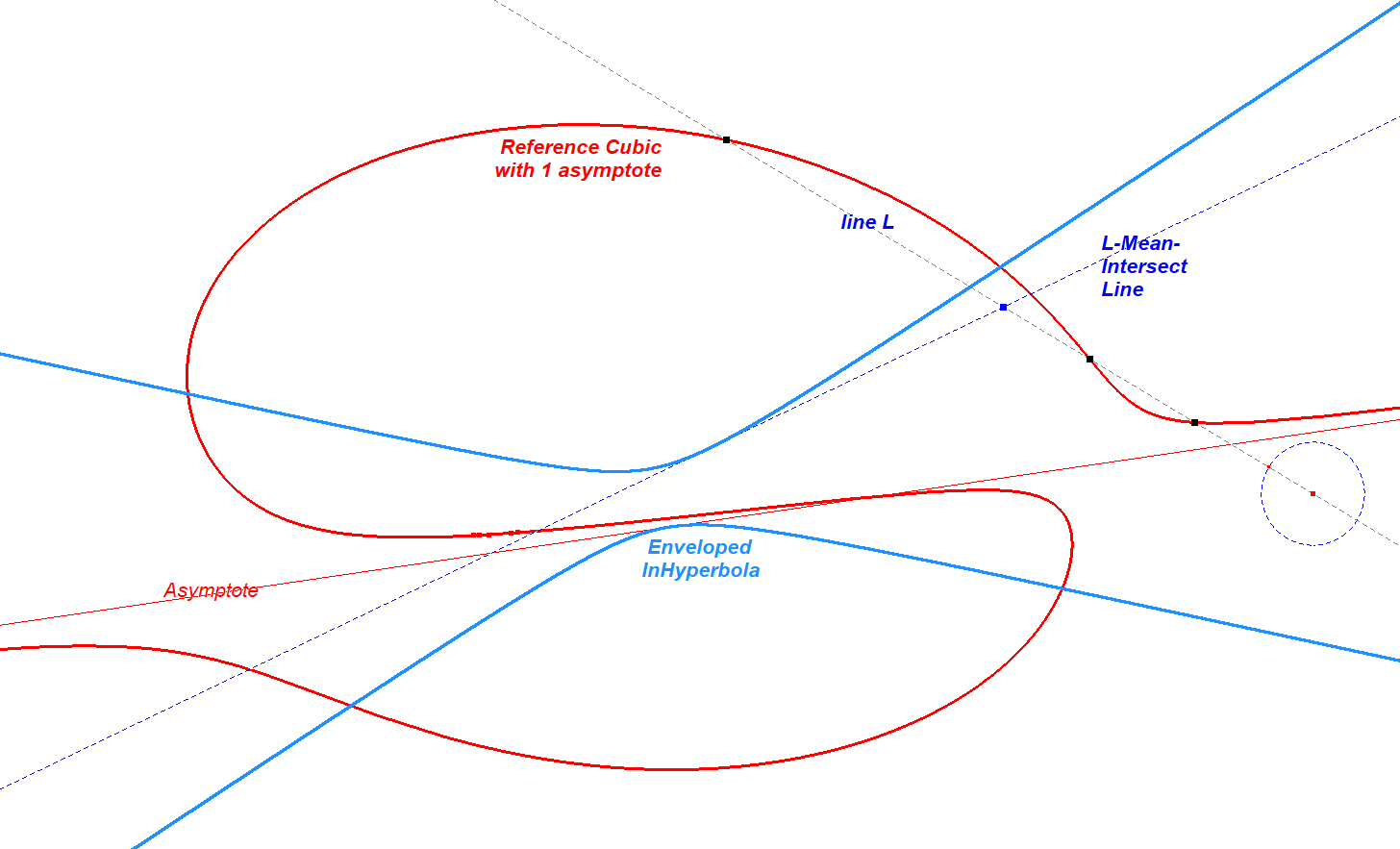
Now that we know this property, when CU has only one real asymptote, the Steiner InEllipse can be constructed as the envelope of L-Mean Intersect Lines. In this case, instead of an InEllipse, it becomes an InHyperbola touching the one and only real asymptote. As a matter of algebraic consistency, the InHyperbola will also touch the imaginary asymptotes, but in the imaginary realm.

Infovisual CU-L-L2-infovisual-cvt-03.png

CU-L-L2 Mean Line of Intersection-30.fig

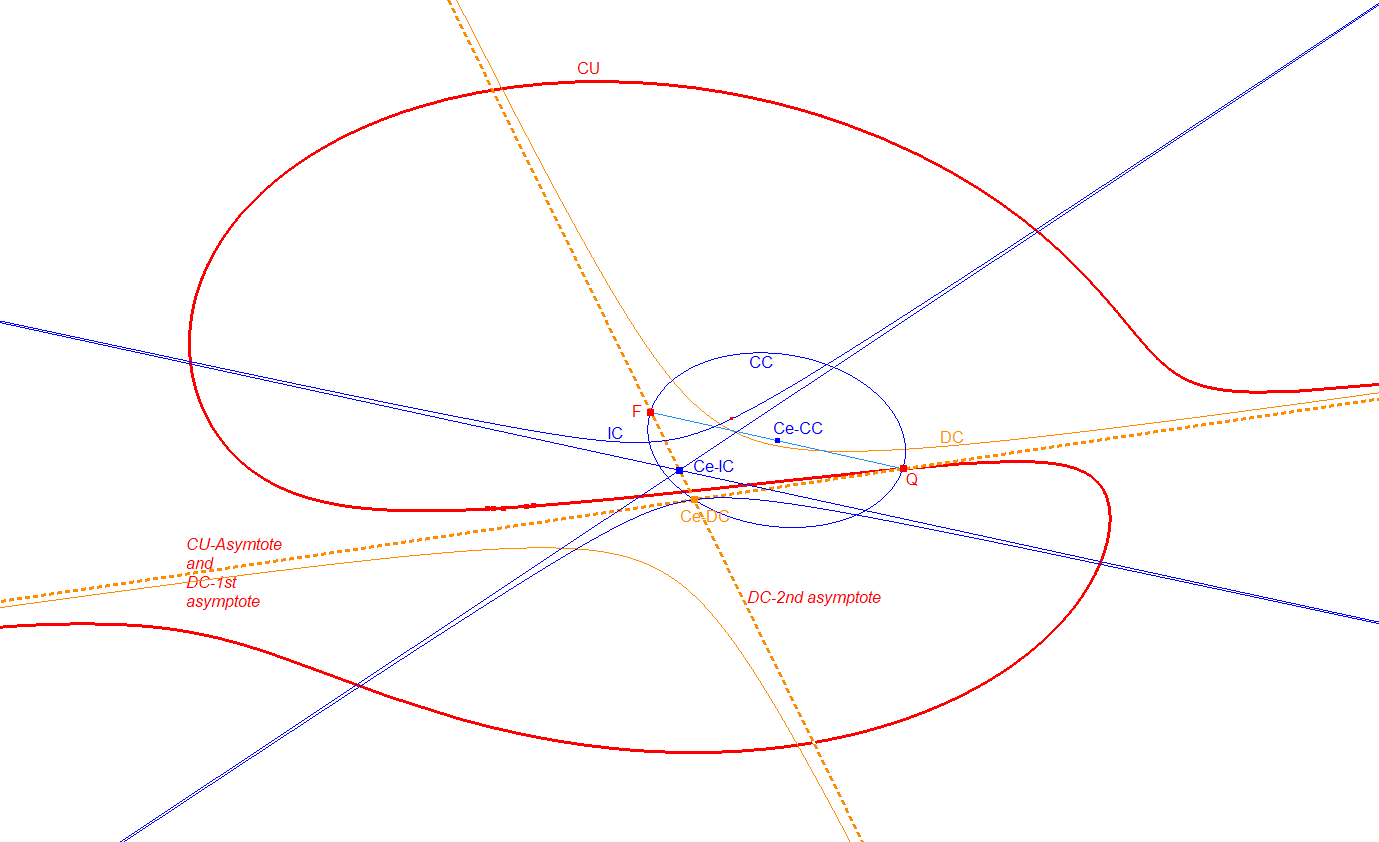
This inconic that can be determined now for all appearances of a cubic has several incidences with CU and 2 other conics, the Diametral Conic CU-IP-Co1 and the Central Conic/QF Conic CU-IP-Co2.

Infovisual CU-L-L2-infovisual-cvt-04.png

CU-L-L2 Mean Line of Intersection-31.fig

The center Ce-DC of the Diametral Conic DC lies on IC.

The 2 asymptotes of the Diametral Conic are Asy1 and another line passing through the center of IC.

This 2nd DC-asymptote contains:

  • obviously the Center of IC
  • the center of DC
  • the Point F diametral to Q on the Central Conic CC

The Center of DC also lies on the Central Conic CC.

Note: F is also the intersection point of the imaginary 2nd and 3rd asymptotes of reference cubic CU.



Estimated human page views: 6

Scroll naar boven