CU-P-Co1 P-Polar Conic of a Cubic
The Polar Conic of some point P wrt to a Cubic is the equivalent of the Polar Line of some point P wrt to a Conic.
In algebraic geometry, the first polar, or simply polar of an algebraic plane curve C of degree n with respect to a point P is an algebraic curve of degree n-1 which contains every point of C whose tangent line passes through P.
When the plane curve is a cubic it is the 1st derivative of the function of the Reference Cubic CU being a function of 2nd degree or a conic. This conic will contain every point of CU whose tangent line passes through P.
Construction
- Given Reference Cubic CU and a random point P on CU.
- Draw 4 lines through P intersecting CU in a 2nd and 3rd point resp. (S1a, S1b), (S2a, S2b), (S3a, S3b), (S4a, S4b).
- Then construct the points Hi=Harmonic Conjugate of P wrt (Sia, Sib) for i=1,2,3,4.
- The conic (P, H1, H2, H3, H4) will be the P-Polar Conic of P wrt CU.
This specific construction method for the Polar Conic wrt a cubic can be found at [83], 2.15 page 45.
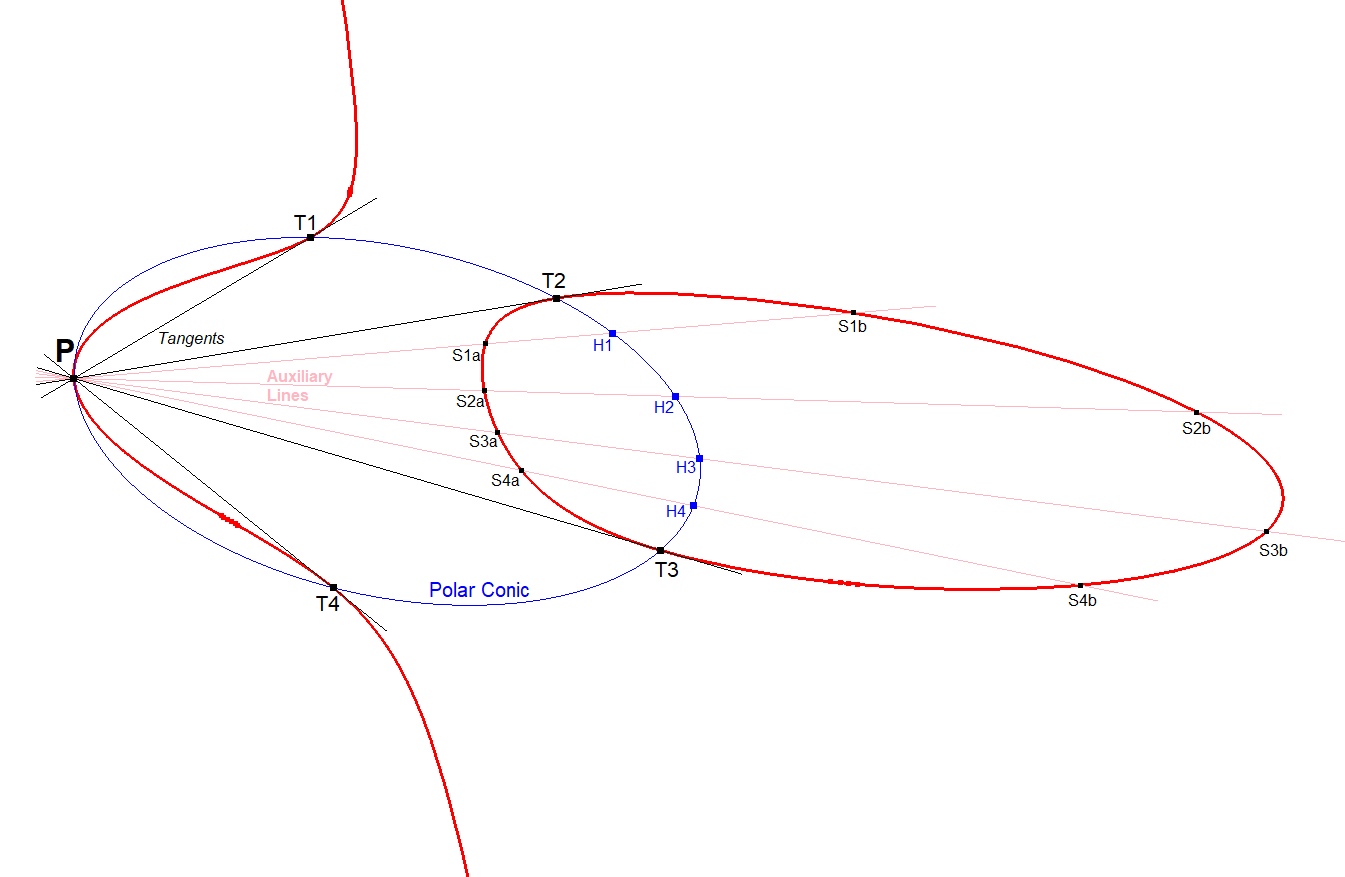
CU-P-Co1 CU P-Polar Conic-01.fig
As can be seen in the picture
- the P-Polar Conic is tangent to CU at P
- the P-Polar Conic intersects CU in the points of tangency of the tangents from P to CU.
The total number of intersection points of cubic and conic should be 6 according to Bezout’s Theorem.
This is exactly what happens. There are these 6 points: P (counting twice because of tangency), T1, T2, T3, T4.
Applications
- A P-Polar Conic yields 4 P-Points of tangency P1,P2,P3,P4 forming a quadrangle QA(P1,P2,P3,P4). The vertices of the Diagonal Triangle QA-Tr1 of this QA also lie on the cubic. The involutary Conjugate (QA-Tf2) of this QA maps a point P on CU to another point on CU. See CU-P-Tf1 and CU-IP-Tf1.
- The IPi-Polar Conic (IPi is the Infinity Point of the ith Asymptote (i=1,2,3) of the cubic) CU-IP-Co1 is called “Conique Diamétrale” by Roger Cuppens. See [63], page 262. It cuts CU in IPi and the 4 Anallagmatic Points CU-IP-4P1.
Estimated human page views: 94
