nL-n-Tf2 nL-Orthopolar

nL-n-Tf2 is the transformation which transforms a random line L into an “Orthopolar” Line in an n-Line.

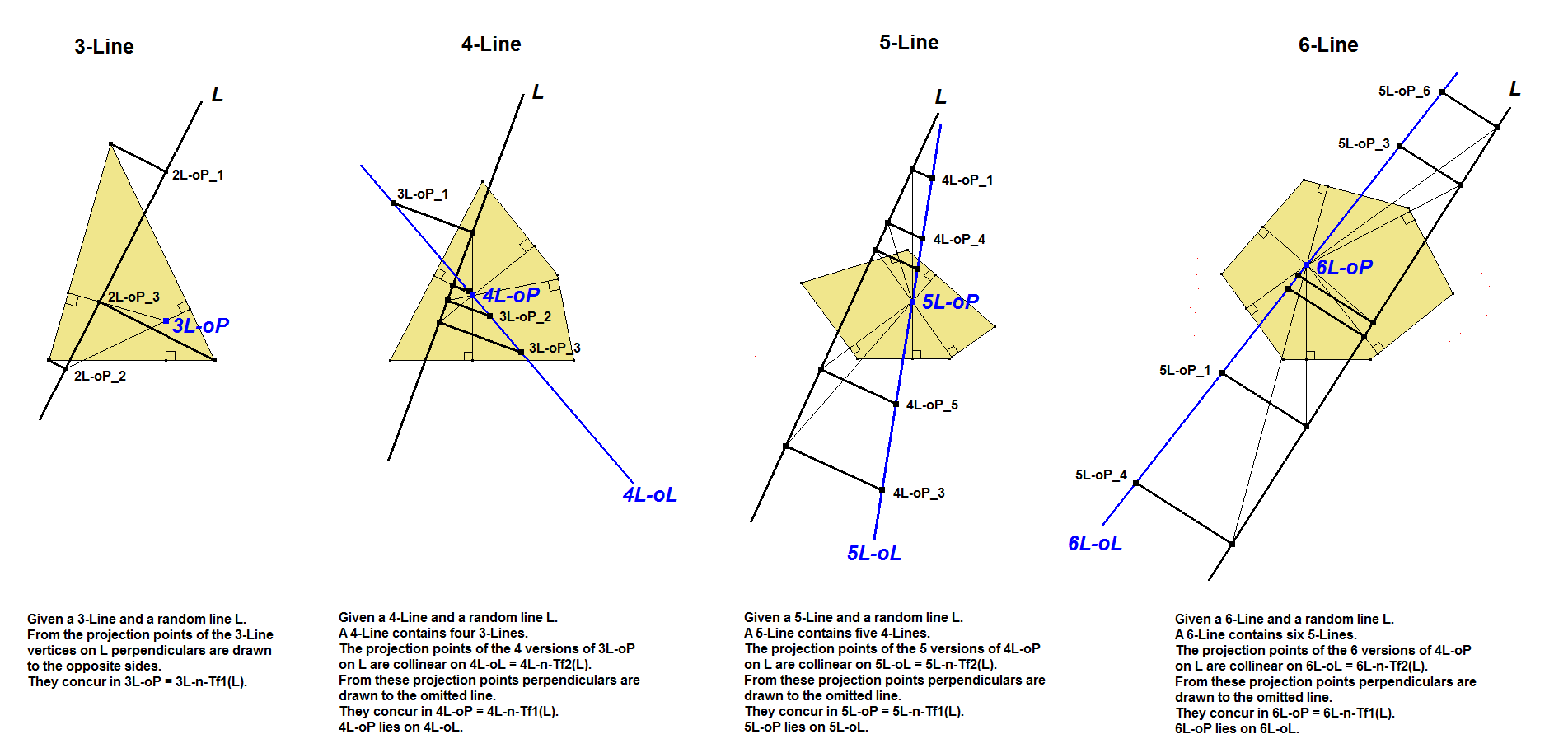
In a 3-Line there is no Orthopolar.

In a 4-Line it is the Orthopolar in a Quadrilateral. See Ref-13. This is the line being made of the four 3L-Orthopoles of the Component Triangles of the 4-Line, which are collinear.

The method for constructing an Orthopole in an n-Line can be made recursive by using the same method as in a 4-Line. It is the line being made of the n (n-1)L-Orthopoles (n-1)L-n-Tf1(L) of the Component (n-1)-Lines of the n-Line, which are collinear.

See figure below. See [34], QFG#2086.

Conjecture

• Let L0 be a random line.
• Let nLL be the n-Line made up from the n versions of (n-1)L-n-Tf2(L0).
• Let nLL-n-Tf2 be the nL-n-Tf2 transformation wrt nLL.
• nLL-n-Tf2 has these special properties:
  • nLL-n-Tf2(La) // nLL-n-Tf2(Lb), where La and Lb are two different random lines.
  • nLL-n-Tf2(L0) will be a line passing through the intersection point of L0 and nL-n-Tf2(L0) and will be parallel to the lines described in former property.
  • the n versions of (n-1)LL-n-Tf2(L0) coincide with nLL-n-Tf2(L0).
  • the n versions of (n-1)LL-n-Tf2(LLi) coincide with a line // nLL-n-Tf2(L0), where LLi is the omitted line of nLL and i=1, …, n.

Estimated human page views: 281