5P-s-Tf4: 5P-Orthopolar Line
5P-s-Tf4 transforms a line into another line.
Construction:
- Let L be a random line.
- 5P-s-Tf4(L) is the locus of 5P-s-Tf3(P) with P varying on L.
Another construction uses QA-Tf6(L) = Quang Duong’s Transformation.
A 5-Point contains 5 4-Points (Quadrangles). The 5 versions of QA-Tf6(L) for these Quadrangles are lying on 5P-s-Tf4(L).
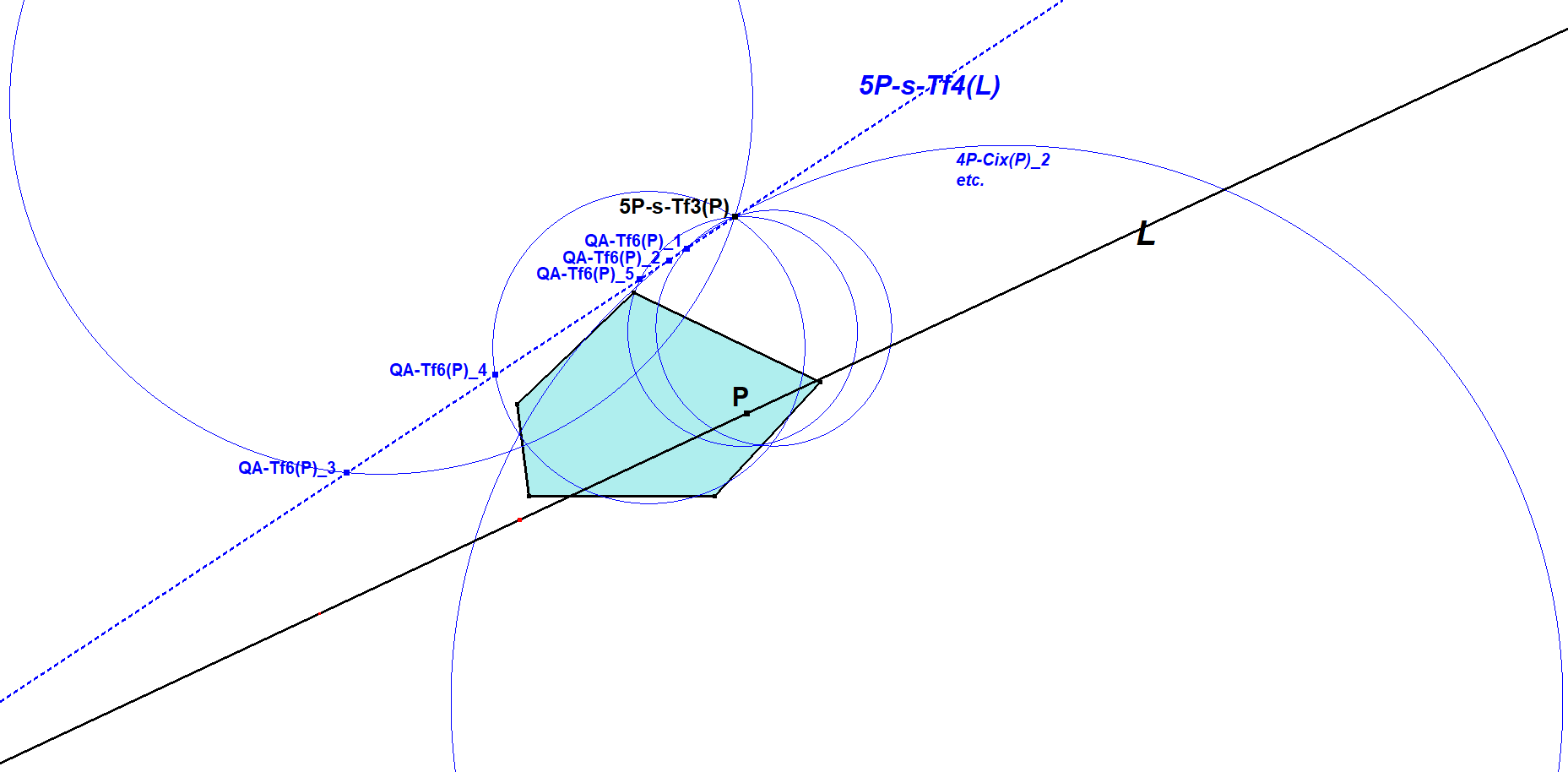
Properties
- 5P-s-Tf4 of lines L through a point P give the line pencil of 5P-s-Tf3(P). See [34], Eckart Schmidt, QFG#2792.
- Points L ∩ 5Ps-sTf4(L) for a line pencil of point P give an orthogonal hyperbola through 5P-s-P1, P and Tf3(P). Its center is in the midpoint of P and Tf3(P). Its asymptotes are parallel to the axes of 5P-s-Co1. See [34], Eckart Schmidt, QFG#2792.
Estimated human page views: 337
