QA-P18: Involutary Conjugate of QA-P19

QA-P18 is the Involutary Conjugate of QA-P19.

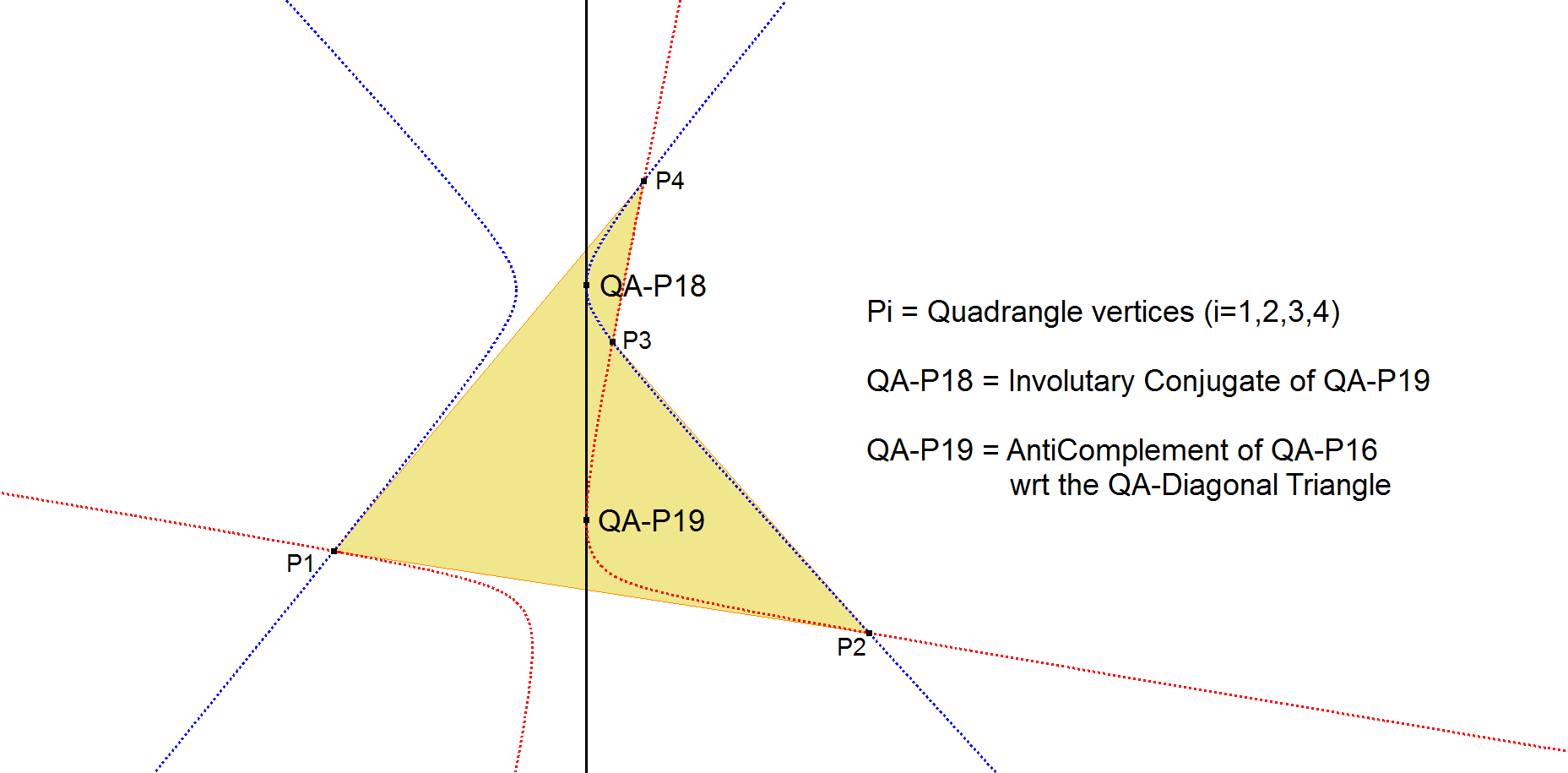
As a consequence the line QA-P18.QA-P19 is the common tangent of the circumscribed conics P1.P2.P3.P4.QA-P18 and P1.P2.P3.P4.QA-P19.

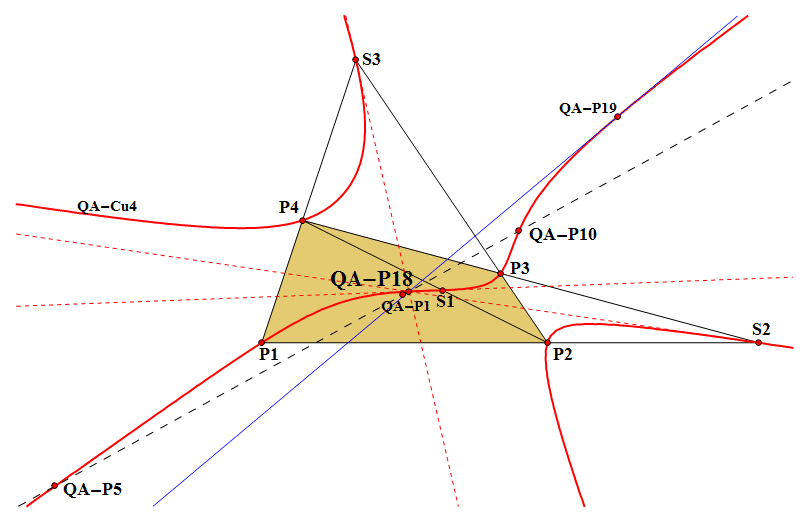
QA-P18 is the intersection point of the tangents at the vertices of the QA-Diagonal Triangle and QA-P19 to the QA-DT-P19 Cubic (QA-Cu4).

1^st CT-coordinate

p (q² + r²) (2 p + q + r) (p² + p q + p r – q r)

1^st DT-coordinate

p² / (-p² + q² + r²)

Properties

• QA-P18 lies on this QA-line:
  • QA-P1.QA-P5 = QA-L3.
• QA-P18 is the Involutary Conjugate (see QA-Tf2) of QA-P19.
• QA-P18 lies on the line QA-P1.QA-P5.
• QA-P18 lies on the QA-DT-P19 Cubic (QA-Cu4).
• QA-P18 also lies on the tangent at QA-P19 to the QA-DT-P19 Cubic (QA-Cu4), which is also the tangent at QA-P19 to the Conic (P1,P2,P3,P4,QA-P19),
• which is also the tangent at QA-P18 to the Conic (P1,P2,P3,P4,QA-P18).
• The tangents to QA-Co5 at QA-P16 and QA-P17 intersect at QA-P18 (Randy Hutson, July, 2012).

Estimated human page views: 526