QA-Tf1

QA-Tf1: QA-Line Involution Center

General Information

In mathematics, an involution (or involutory function) is a function f that is its own inverse:

f(f(x))=x for all x in the domain of f.

A line involution involves pairs of points on a line such that the product of their distances from a fixed point P is a constant. This point P is called the center of involution.

Let (A0,A1) and (B0,B1) be two pairs of points on a line, and let O be a fixed point such that the product of the distances from O is a constant c.

According to the definition of line involution:

A0O⋅A1O = B0O⋅B1O = c.

When the points A0, A1, and the constant c are known, we can determine the corresponding point B1 for any given point B0.

Performing the same calculation starting from B1 yields its mate B0.

This symmetry makes the transformation an involutory function, since:

f(f(P))=P.f(f(P)) = P.

When B0=B1, we say that B0 is a double point. Every line involution has exactly two double points, and their midpoint is the center of involution, denoted by O.

Construction

For a Line Involution let (A0, A1) and (B0, B1) be two pairs of points and ciA and ciB circles with these diameters.

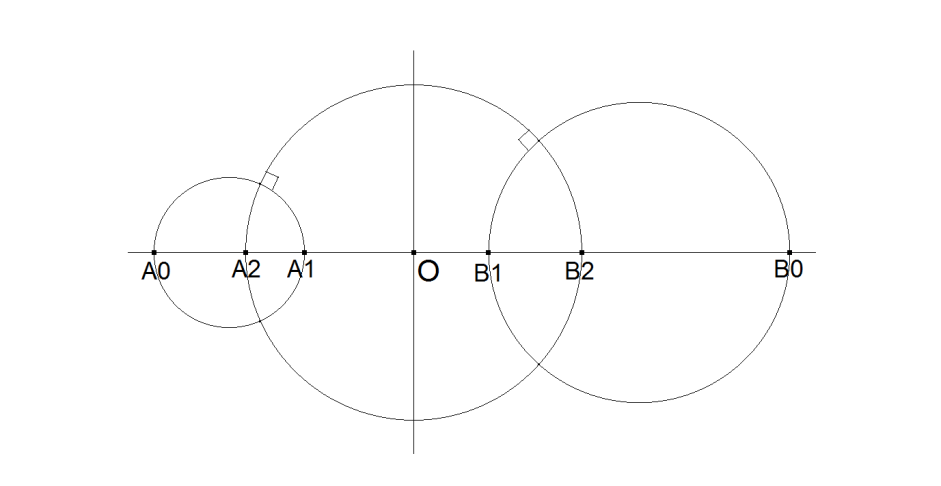
The radical axis of ciA and ciB cuts the line in the Involution Center O.

A circle with center O perpendicular to ciA and ciB cuts the line in the two Doublepoints A2, B2.

Another construction can be found in [19].

Desargues’ Involution Theorem

A figure consisting of 4 points and their 6 connecting lines is called a (complete) Quadrangle. The 4 points are the vertices. The 6 connecting lines are the sides of the (complete) Quadrangle. Sides in a (complete) Quadrangle that have no vertices in common are called opposite sides.

Desargues’ Involution theorem states that the points of intersection of a line with the three pairs of opposite sides of a complete Quadrangle and a conic section circumscribed about the complete quadrangle form the pairs of an involution (see [7]).

Normally 2 pairs of points describe an involution. Desargues describes in his theorem 4 pairs of points all describing the same involution.

If we restrict ourselves to the 3 pairs of points generated from 3 sets of opposite sides we can deduce that when a line crosses a quadrangle it generates a unique Line Involution with an involution center and 2 Doublepoints (when real).

Consequently every line crossing a Quadrangle has an Involution Center and 2 Doublepoints (real or imaginary).

This line involution is a property of a Quadrangle (and not of a Quadrilateral as might be suspected).

In the QA-environment this will be called a QA-Line Involution.

Coordinates of the Involution Center and Doublepoints on some line L

Let L be a random line with barycentric coefficients (l:m:n).

Coordinates of Involution Center on L in CT-notation:

(m n p (m q + n r – l (q + r)) : l n q (l p + n r – m (p + r)) : l m (l p + m q – n (p + q)) r)

Coordinates of both Doublepoints on L in CT-notation:

(m n p (m q + n r) : -l m n p q – n W : -l m n p r + m W)

(m n p (m q + n r) : -l m n p q + n W : -l m n p r – m W)

where W = √(-l m n p q r (l p + m q + n r))

Properties

- - QA-Tf1(QA-L3) = QA-P22.
  - QA-Tf1(QA-L4) = QA-P1.QA-P6 ^ QA-P11.QA-P38 ^ QA-P22.QA-P29.
  - QA-Tf1(QA-L1), QA-Tf1(QA-L3), QA-Tf1(QA-L4), QA-Tf1(QA-L6) lie on QA-Cu6.
  - QA-Tf1(QA-L9) lies on QA-Cu1.
  - Let L be a random line and Q1, Q2 the Doublepoints created by the generated QA-Line Involution.
  - When Q1 and Q2 are real Doublepoints then line L is tangent in Qi at the conic (P1,P2,P3,P4,Qi) and also tangent at the QA-DT-cubic with pivot Qi.

Addendum:

Calculations:

Let (A0,A1) and (B0,B1) be 2 pairs of points on a line that create a Line Involution with center O.

Then according to the definition: d(A0,O) * d(A1,O) = d(B0,O) * d(B1,O).

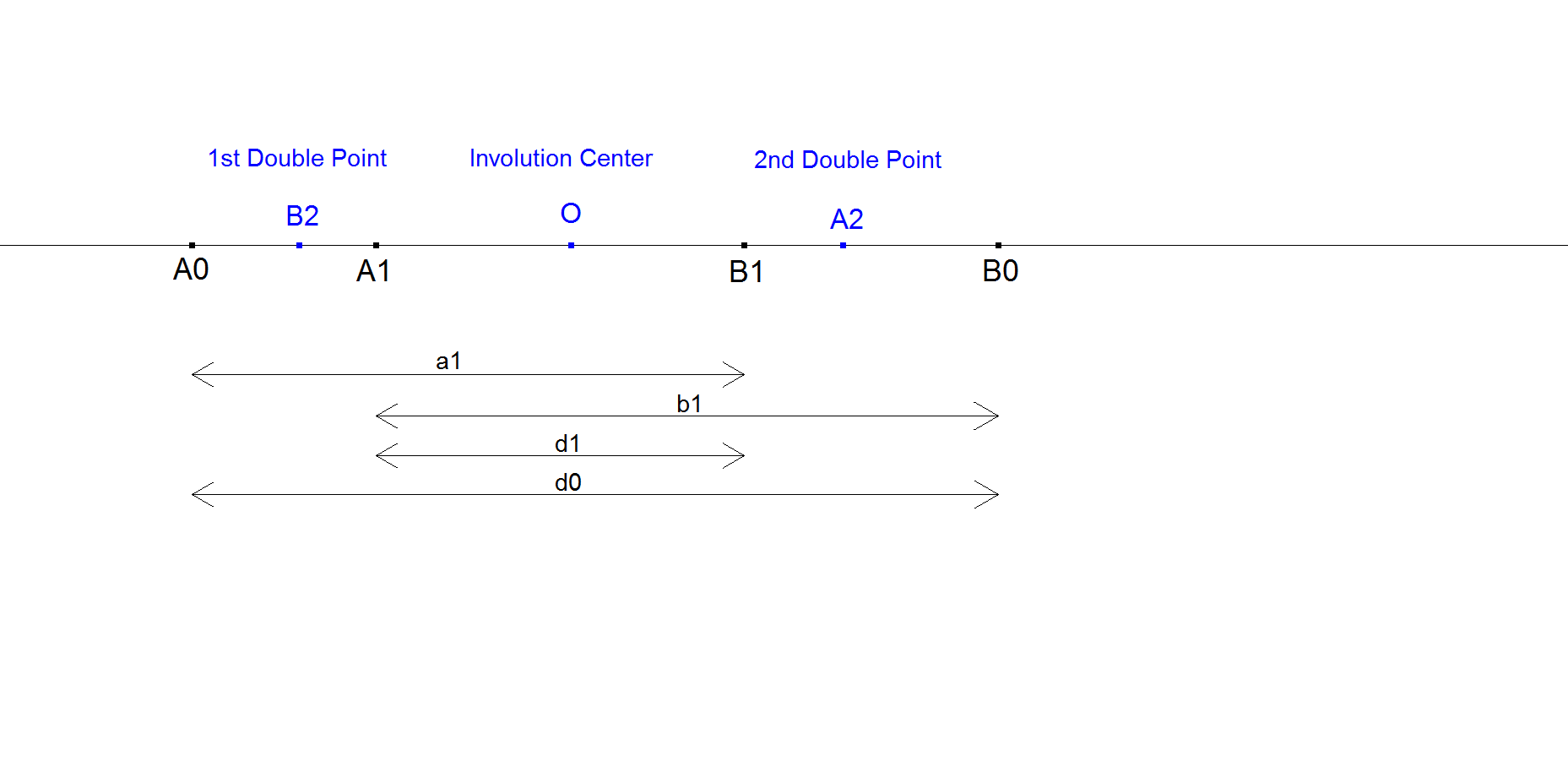
Let A2, B2 be the corresponding Doublepoints. Now:

d(A0,A2) = (a1*d1 – √ [d0*d1*a1*b1]) / (a1+b1)
d(A0,B2) = (a1*d0 + √ [d0*d1*a1*b1]) / (a1+b1)
d(B0,B2) = (b1*d0 – √ [d0*d1*a1*b1]) / (a1+b1)
d(B0,A2) = (b1*d1 + √ [d0*d1*a1*b1]) / (a1+b1)

The center of involution O is given by:

d(A1,O) = a1*d0 / (a1+b1)
d(B1,O) = b1*d0 / (a1+b1)
and d(A2,O) = d(B2,O) = √ [d0.d1.a1.b1] / (a1+b1)

Let (A0,A1) and (B0,B1) be 2 pairs of points on a line that create a Line Involution with center O.

Let A2 and B2 be the respective Doublepoints.

When (A0,A1) and B2 are known then we can calculate the position of A2:

Let d3 = d(B2,A0) and d4 = d(B2,A1)
then e0 = d(A2,A0) = (d3*d3-d3*d4)/(d3+d4),
and e1 = d(A2,A1) = (d4*d4-d3*d4)/(d3+d4).

Estimated human page views: 631