QA-P38

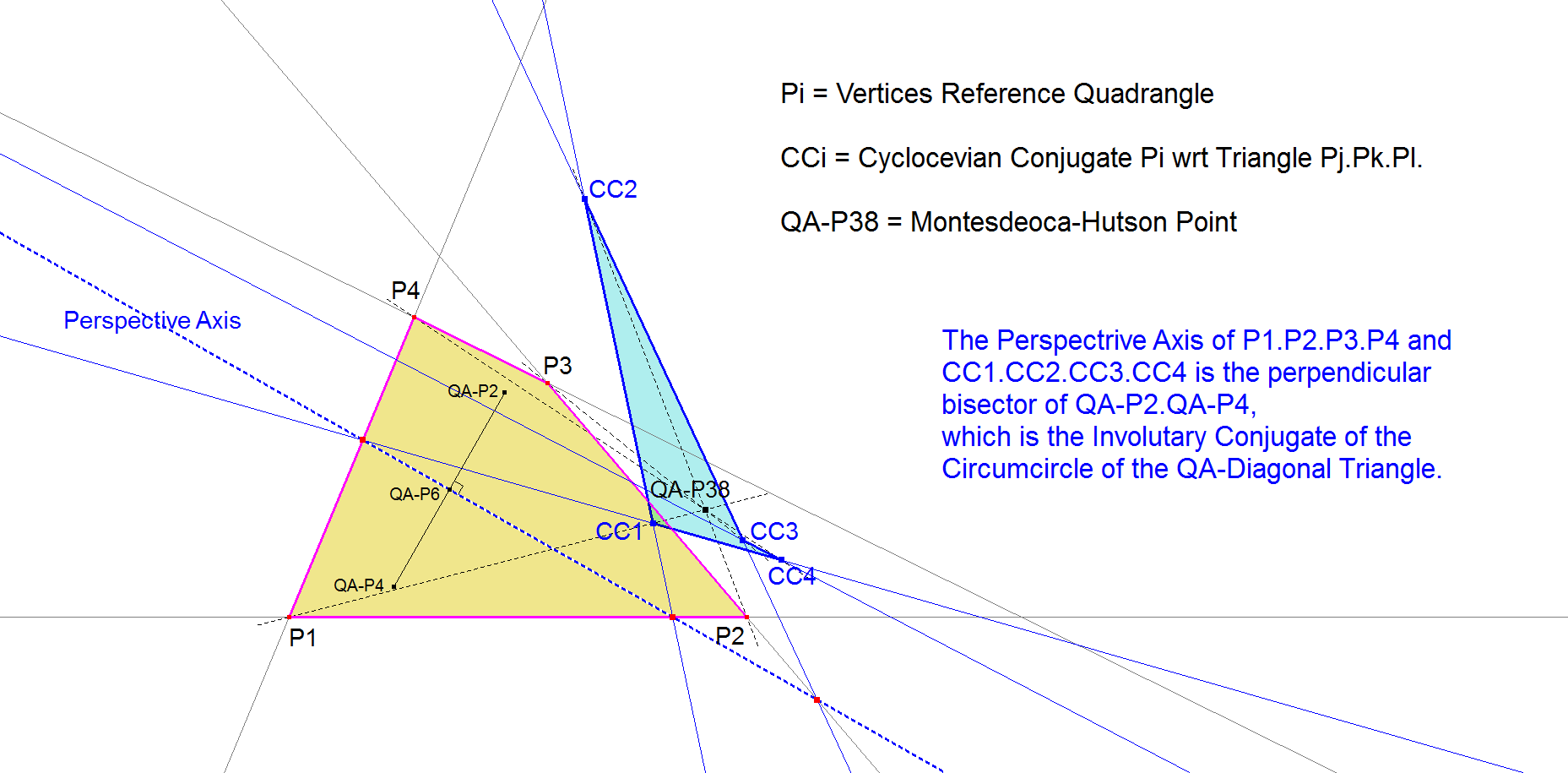
QA-P38: Montesdeoca-Hutson Point

QA-P38 is the Perspector of the Reference Quadrangle with the Cyclocevian Quadrangle.

The Cyclocevian Quadrangle CC1.CC2.CC3.CC4 is defined by:

CCi = Cyclocevian Conjugate of Pi wrt Pj.Pk.Pl for all combinations of (i,j,k,l) ∈ (1,2,3,4).

The definition of Cyclocevian Conjugate can be found at [13].

This point was separately found by Angel Montesdeoca (Hyacinthos message 21075, see[11]) and Randy Hutson (private mail to author EQF) in the same week (June, 2012).

Construction (by Angel Montesdeoca):

Let S1.S2.S3 be the QA-Diagonal Triangle of the Reference Quadrangle P1.P2.P3.P4.

For each vertex Pi, we take the triangle TjTkTl, where Tj the intersection of the sidelines PkPl with circumcircle of the triangle S1.S2.S3 (other than S1, S2, S3).

Qi = Perspector of the triangle PjPkPl and TjTkTl.

QA-P38 is the common intersection point of lines Pi.Qi.

1st CT-Coordinate

a² q r (p + q)(p + r) (-2 p + q + r) + b² p r (p + q) (q + r) (2 p – q + r) + c² p q (p + r) (q + r) (2 p + q – r)

———————————————————————————————————————————————————————–

-a² q r (p + q)(p + r) + b² p r (p + q) (q + r) + c² p q (p + r) (q + r)

1st DT-Coordinate

a² (-c⁴ p² q² – b⁴ p² r² + a⁴ q² r²)

Properties

QA-P38 lies on the line through S and QA-P11,

where S = the intersection point QA-P1.QA-P6 ^ QA-P22.QA-P29.
S is also the Involution Center of the line QA-P1.QA-P6 wrt the Reference Quadrangle.

QA-P38.QA-P11 // QA-P1.QA-P32 // QA-P2.QA-P4 // QA-P7.QA-P8 // QA-P12.QA-P24.
QA-P38 = Perspector CycloCevian Quadrangle CC1.CC2.CC3.CC4 with Reference Quadrangle P1.P2.P3.P4 (definition Randy Hutson).

The Perspectrix (Perspective Axis) of P1.P2.P3.P4 and CC1.CC2.CC3.CC4 is the perpendicular bisector of QA-P2.QA-P4 (QA-L9), which happens to be the Involutary Conjugate (QA-Tf2) of the Circumcircle of the QA-Diagonal Triangle (QA-Tr1).

QA-P38 = TCC-Perspector Pi wrt QA-Diagonal Triangle (i=1,2,3,4)

(note Angel Montesdeoca). Definition of the TCC-Perspector can be found at [12] in the description just before X(1601).

Let Sij = 2nd intersection point of the line Pi.Pj and the circumcircle of the QA-Diagonal Triangle. Now QA-P38 = S12.S34 ^ S13.S24 ^ S14.S23 (note Angel Montesdeoca). This is a general property not only for QA-Ci1 wrt the 6 sides of a Quadrangle, but also for each QA-DT-conic wrt the 6 sides of a Quadrangle. See QA-Co-1.

Estimated human page views: 671