QA-Tf17: 1^st QA-Hung’s Transformation

QA-Tf17 maps a line into a line.

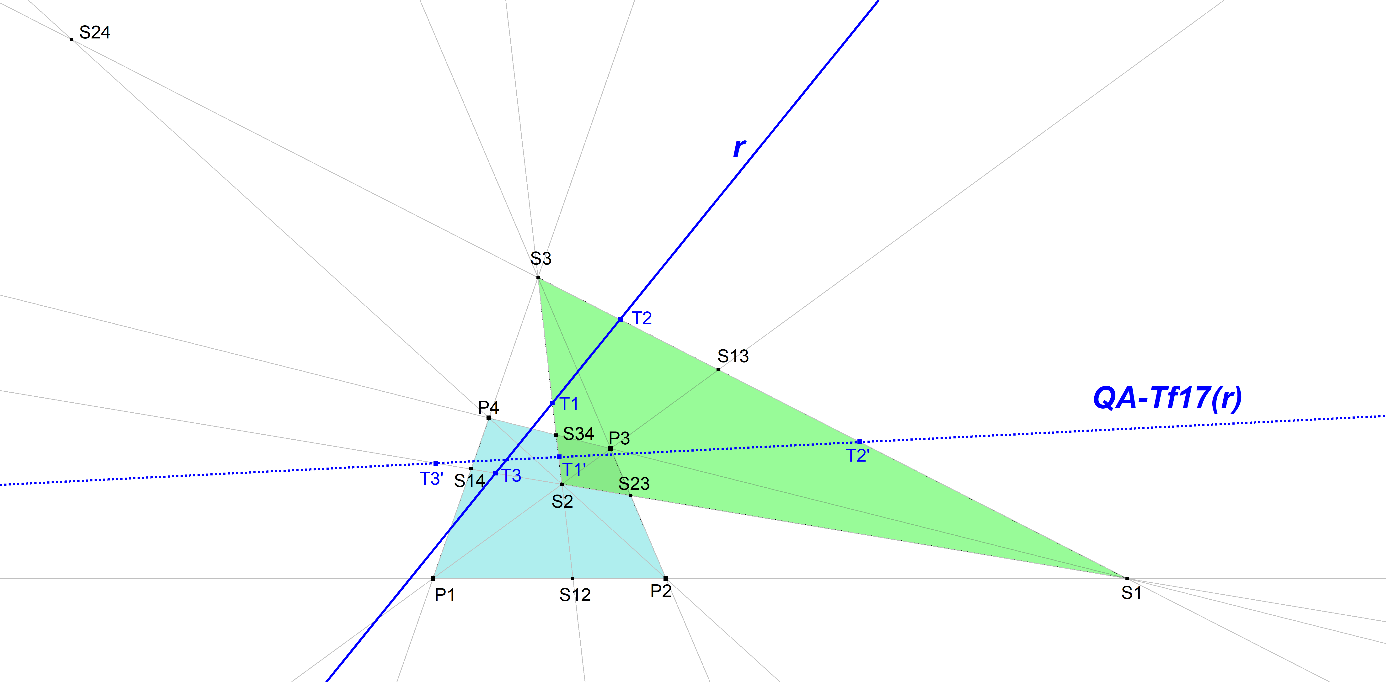
Let P1, P2, P3, P4 be the defining Quadrangle Points.

Let S1 = P1P2 ^ P3P4, S2 = P1P3 ^ P2P4 and S3 = P1P4 ^ P2P3.

Line S2S3 meets lines P1P2 and P3P4 at S12 and S34.

Line S1S2 meets lines P1P4 and P2P3 at S14 and S23.

Line S3S1 meets lines P1P3 and P2P4 at S13 and S24.

r is a random line.

r meets lines S1S3, S3S2, S2S1 at T2, T1, T3.

Construct T1′, T2′, T3′ such that

• (S12,S34;T1,T1′) = -1
• (S14,S23;T3,T3′) = -1
• (S13,S24;T2,T2′) = -1

Then T1′, T2′, T3′ are collinear on a line QA-Tf17(r).

This transformation was found by Tran Quang Hung. See [34], QFG#3711.

CT-coordinates of QA-Tf17(r), where r=(l:m:n)

( q r (l² p² – l m p q – m² q² – l n p r – m n q r – n² r²) :

-p r (l² p² + l m p q – m² q² + l n p r + m n q r + n² r²) :

-p q (l² p² + l m p q + m² q² + l n p r + m n q r – n² r²) )

Properties

• QA-Tf17(QA-Tf17( r )) = r. See [34], QFG#3717.
• QA-Tf17(r) = QL-Tf2 of the dual QL as described at QA-8/QL-8. See [34], QFG#3718.
• For lines L of a line pencil wrt a point P, QA-Tf17(L) envelopes a conic tangent at QA-Tr1 in the cevian points of QA-Tf2(P). Example: Inscribed Steiner ellipse for QA-P16. See [34], QFG#3713
• QA-Tf17(Infinity Line) = QA-Lx = line through the midpoints of (S12,S34), (S13,S24), (S14,S23). QA-Lx is a line // QA-P1.QA-Tf2(IP(QA-P1.QA-P16)) // QA-P5.QA-Tf2(IP(QA-P5.QA-P17)) // QA-P10.QA-Tf2(IP(QA-P10.QA-P16)) // QA-P19.QA-Tf2(IP(QA-P1.QA-P5)), where IP denotes “Infinity Point”. See [34], QFG#3717.

Estimated human page views: 213