QA-Tf7 QA-Trilinear Pole

Let P1.P2.P3.P4 be a quadrangle. Let L be a random line. Let T1 be trilinear pole of L wrt triangle P2.P3.P4.

Similarly, we have T2, T3, T4. Then lines P1.T1, P2.T2, P3.T3, P4.T4 are concurrent.

This transformation was found by Tran Quang Hung. See [34], QFG#2084.

It is a transformation with very simple coordinates.

The equivalent of this transformation in a quadrilateral is QL-Tf6.

QA-Tf7 and QL-Tf6 have corresponding coordinates (interchange (p:q:r) with (l:m:n)).

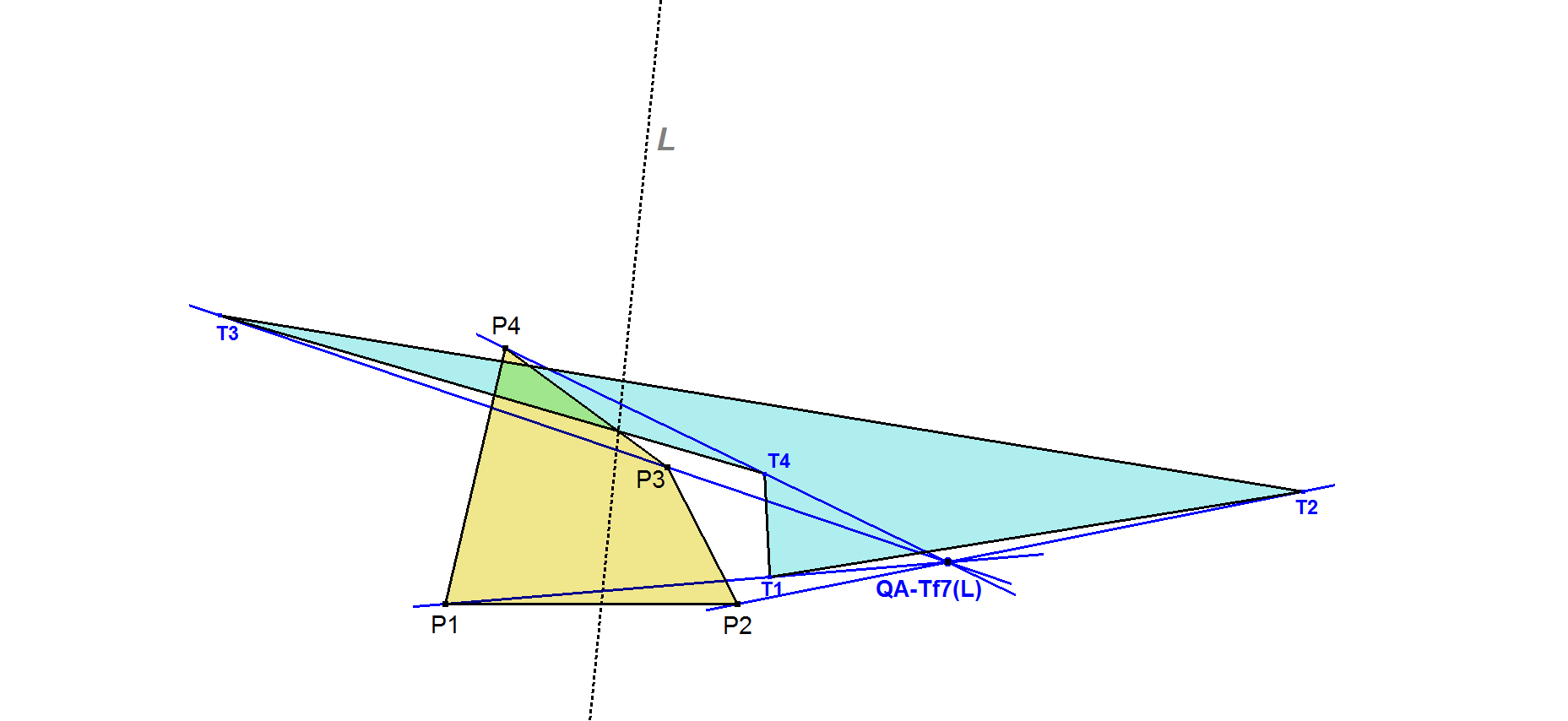
Note that the Quadrangles P1.P2.P3.P4 and T1.T2.T3.T4 are perspective with perspector QA-Tf7(L) and perspectrix L. So this transformation maps the perspectrix into the perspector of this perspective quadrangles.

Given the perspector P there is an inverse transformation QA-Tf7R mapping the perspector into 3 possible related perspectrices Li (i=1,2,3).

For further details and properties see [34], QFG#2139.

CT-coordinate:

Given Line L(x:y:z), then coordinates QA-Tf7(L) are:

(y z (2 p x + q y + r z) : x z (p x + 2 q y + r z) : x y (p x + q y + 2 r z))

Properties

• QA-Tf7(L) is the concurrent point of the 3 versions of QL-Tf2(L). See QA-3QG1.
• QA-Tf7(QA-L9) = QA-P38.
• QA-Tf7(L) = ConicPerspector[QA-Tf2(L)]. See QA-Co-1 and see [34], QFG#2094.

Estimated human page views: 380