QA-Tf8 QA-Orthopolar Line

Let P1.P2.P3.P4 be a Quadrangle and let L be a random line.

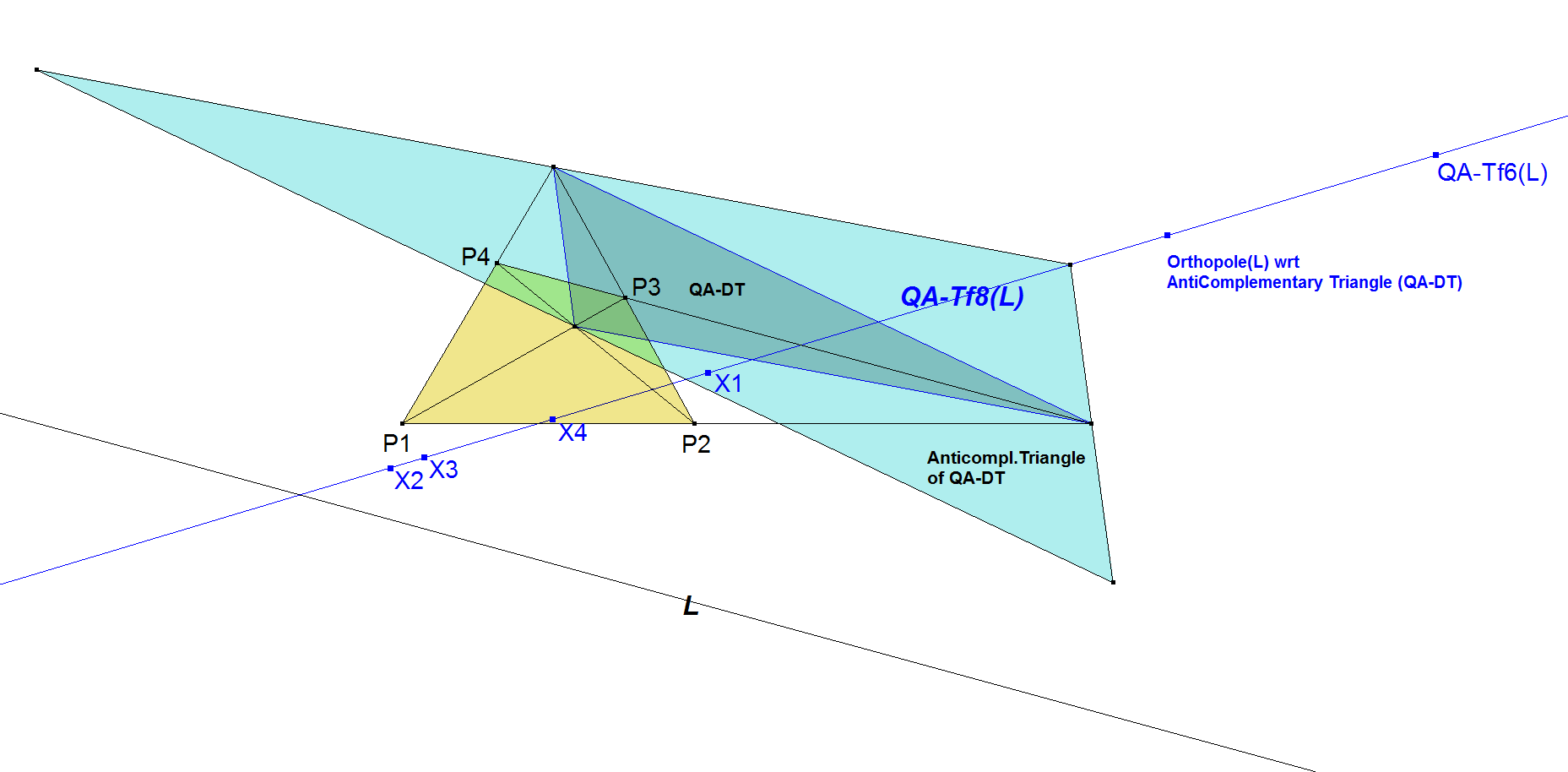
Let X1,X2,X3,X4 be the Orthopoles (for definition see [13]) of L resp. wrt triangles (P2,P3,P4), (P3,P4,P1), (P4,P1,P2), (P1,P2,P3).

X1, X2, X3, X4 are collinear on a line being called the QA-Orthopolar Line, which is QA-Tf8(L).

CT-Coordinates

Let L=(l:m:n), then 1^st coordinate of QA-Tf8(L) is:

– q r (l SB – n SB + l SC – m SC) (SA SB + SA SC + SB SC) l (m – n)

+p r (m SA – n SA – l SC + m SC) (m² SA² – 2 m n SA² + n² SA² + l² SA SB + l m SA SB – 2 l n SA SB – m n SA SB + n² SA SB + l² SA SC – l m SA SC + m² SA SC – m n SA SC + l m SB SC – m n SB SC)

+p q (m SA – n SA + l SB – n SB) (m² SA² – 2 m n SA² + n² SA² + l² SA SB – l n SA SB – m n SA SB + n² SA SB + l² SA SC – 2 l m SA SC + m² SA SC + l n SA SC – m n SA SC + l n SB SC – m n SB SC)

Properties

• QA-Tf6(L) lies on QA-Tf8(L). See [34], QFG#1186.
• The Orthopole X of the Anticomplementary Triangle of QA-Tr1 lies on QA-Tf8(L). See [34], Ngo Quang Duong, QFG#1229. When L= QL-L5 (Eulerline of QA-Tr1), then X = a point on QA-Ci1, the circumcircle of QA-Tr1. Actually X = ETC-point X(110) of the Diagonal Triangle. When L = QL-L9, then X = point on QA-P23.QA-P33. See [34], QFG#1230.
• When L is a line through QA-P4, then QA-Tf8(L) is a line through QA-P2.

Estimated human page views: 372