QG-L3: The QG-Centroids Line
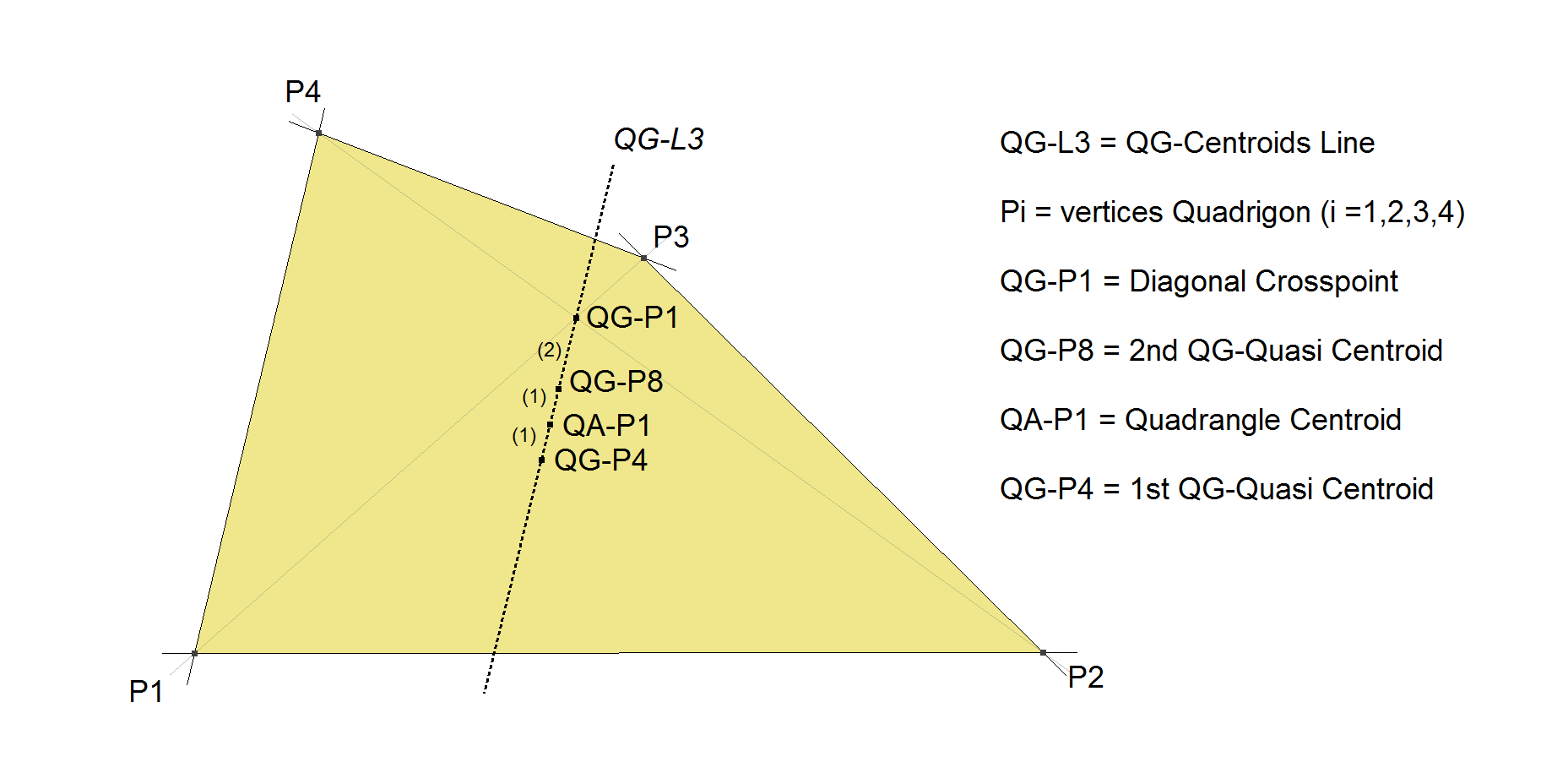
The QG-Centroids Line is the line connecting the 1st and 2nd QG-Quasi Centroids in a Quadrigon. This line is also called the Seebach-Walser Line. See [44].
This line also can be obtained in another way:
Qi divides PiPi+1 with ratio r, Ri divides Pi Pi-1 with ratio r. The sides QiRi yield a Wittenbauer type of parallelogram. The locus of diagonal crosspoints of these parallelograms with variable r, will be QG-L3. See [66], QPG#496 and [67].
CT-Coefficients QG-L3 in 3 QA-Quadrigons
(r (p + 2 q + r) : (p – r) (p + q + r) : -p (p + 2 q + r))
((q – r) (p + q + r) : r (2 p + q + r) : -q (2 p + q + r))
(q (p + q + 2 r) : -p (p + q + 2 r) : (p – q) (p + q + r))
CT-Coefficients QG-L3 in 3 QL-Quadrigons
(l (m – n) (l m + l n – m n) : m (l – n) (-l m + 2 m2 + l n – m n) : -(l – m) n (l m – l n – m n))
(l (m – n) (l m + l n – m n) : -m (l – n) (l m – l n + m n) : (-l + m) n (l m – l n – m n + 2 n2))
(-l (m – n) (2 l2 – l m – l n + m n) : -m (l – n) (l m – l n + m n) : -(l – m) n (l m – l n – m n))
DT-Coefficients QG-L3 in 3 QA-Quadrigons
(r2 (-p2 – q2 + r2) : 0 : p2 (-p2 + q2 + r2))
(0 : r2 (p2 + q2 – r2) : q2 (-p2 + q2 – r2))
(q2 (p2 – q2 + r2) : p2 (p2 – q2 – r2) : 0)
DT-Coefficients QG-L3 in 3 QL-Quadrigons
(l2 – m2 : 0 : m2 – n2)
(n2 – l2 : m2 – n2 : 0)
(0 : l2 – m2 : n2 – l2)
Properties
- These points lie on QG-L3: QG-P1, QG-P4, QG-P8, QG-P15, QA-P1. Three of them are (quasi-)centroids.
- The distance ratios between points QG-P15, QG-P4, QA-P1, QG-P8, QG-P1 are 2:1:1:2 in this order.
Estimated human page views: 662
