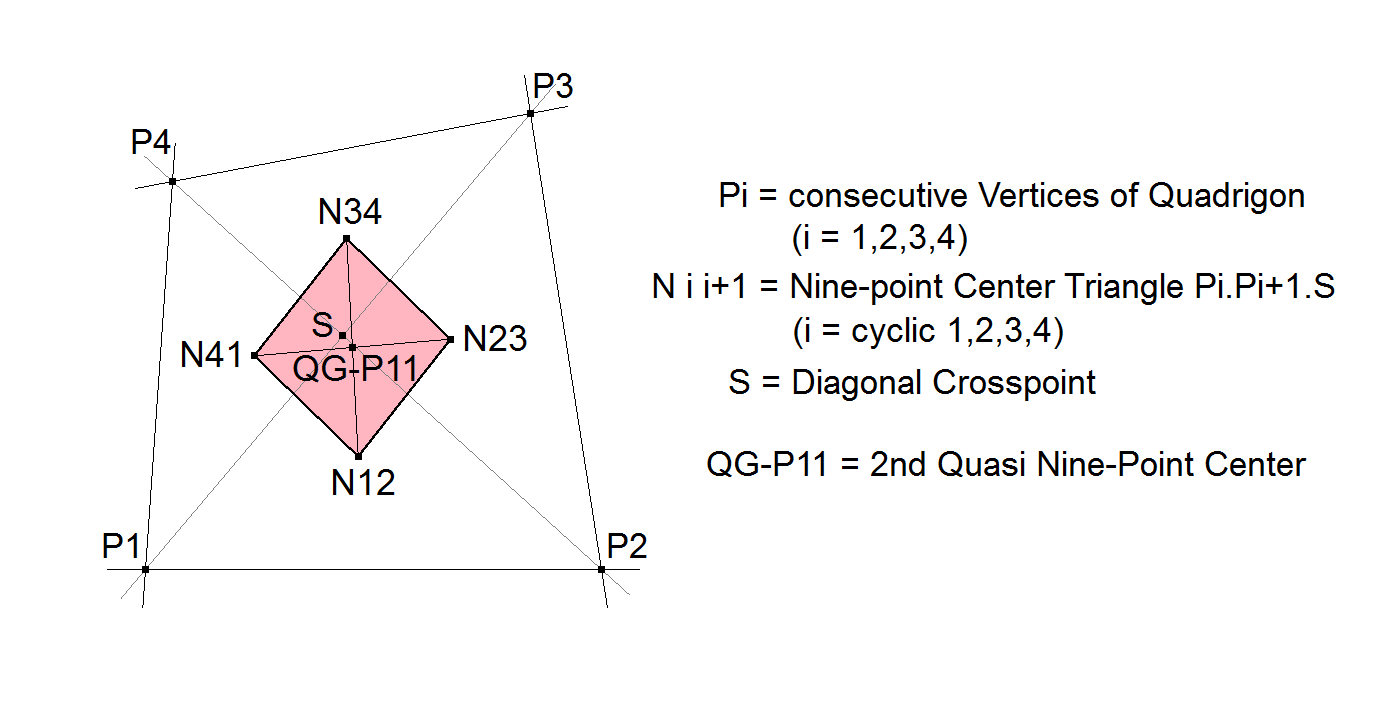
QG-P11 2nd Quasi Nine-point Center
Let P1.P2.P3.P4 be a Quadrigon and let S be its Diagonal Crosspoint QG-P1.
Let Ni i+1 = Nine-point Center of Triangle Pi.Pi+1.S (i = cyclic sequence 1,2,3,4) .
Now is N12.N23.N34.N41 a parallelogram.
QG-P11 is the Center of this parallelogram.
CT-Coordinates QG-P11 in 3 QA-Quadrigons (only coordinates of 1st Quadrigon point are given)
((-24 Δ2 + a2 SA) p2 + (-8 Δ2 – a2 (a2 – c2)) q r + (-8 Δ2 + a2 SA) r2 + p ((-16 Δ2 – (a2 – c2) SB) q + (-24 Δ2 – (a2 + c2) SC) r),
(-8 Δ2 + b2 SB) p2 + (-16 Δ2 + b2 (a2 + SB)) q r + (-8 Δ2 + b2 SB) r2 + p ((-8 Δ2 – (a2 – c2) SA) q + (-16 Δ2 + b2 (a2 + c2)) r),
(-8 Δ2 + c2 SC) p2 + (-16 Δ2 + (a2 – c2) SB) q r + (-24 Δ2 + c2 SC) r2 + p ((-8 Δ2 + (a2 – c2) c2 ) q + (-24 Δ2 – SA (a2 + c2)) r))
CT-Coordinates QG-P11 in 3 QL-Quadrigons (only coordinates of 1st Quadrigon point are given)
(2 a2 m (b2 l2 + c2 l2 – 2 b2 l m + b2 m2) n – 16 Δ2 (-l2 m2 + l m3 + 2 l2 m n – 6 l m2 n + 3 m3 n
– l2 n2 + 3 l m n2 – 3 m2 n2) – 2 a2 (l2 m2 + l2 n2 + m2 n2) SA – 2 l m (b2 m2 + a2 n2 + b2 n2) SB
– 4 c2 l m2 n SC :
2 b2 (a2 + b2 + c2) l m2 n – 16 Δ2 (-l2 m2 + 3 l2 m n – 2 l m2 n – 3 l2 n2 + 3 l m n2 – m2 n2)
– 2 l m (b2 m2 + a2 n2 + b2 n2) SA – 2 b2 (l2 m2 + l2 n2 + m2 n2) SB – 2 m (b2 l2 + c2 l2
+ b2 m2) n SC :
-c2 l (-2 b2 m3 + 4 b2 m2 n + a2 l n2 + b2 l n2 – c2 l n2 – 2 a2 m n2 – 2 b2 m n2) – 16 Δ2 (-3 l2 m2
+ 3 l m3 + 3 l2 m n – 6 l m2 n + m3 n – l2 n2 + 2 l m n2 – m2 n2) – 4 a2 l m2 n SA – 2 m (b2 l2
+ c2 l2 + b2 m2) n SB – 2 c2 m2 (l2 + n2) SC)
CT-Area of QG-P11-Triangle in the QA-environment
(a4 q r (p2 + p q + p r – 3 q r) + b4 p r (p q + q2 – 3 p r + q r) + c4 p q (-3 p q + p r + q r + r2)
– 2 b2 c2 p q r (4 p + q + r) – 2 a2 c2 p q r (p + 4 q + r) – 2 a2 b2 p q r (p + q + 4 r) )
/ (128 Δ (p + q) (p + r) (q + r) (p + q + r))
CT-Area of QG-P11-Triangle in the QL-environment
(+a4 m2 n2 (l – m)2 (l – n)2 (13 l2 m2 – 22 l2 m n – 2 l m2 n + 13 l2 n2 – 2 l m n2 + m2 n2)
+ b4 l2 n2 (l – m)2 (m – n)2 (13 l2 m2 – 2 l2 m n – 22 l m2 n + l2 n2 – 2 l m n2 + 13 m2 n2)
+ c4 l2 m2 (l – n)2 (m – n)2 (l2 m2 – 2 l2 m n – 2 l m2 n + 13 l2 n2 – 22 l m n2 + 13 m2 n2)
+ 2 b2 c2 l2 m n (l – m) (l – n) (m – n)2 (l2 m2 – 14 l2 m n + 12 l m2 n + l2 n2 + 12 l m n2 – 13 m2 n2)
+ 2 a2 c2 l m2 n (m – l) (m – n) (l – n)2 (l2 m2 + 12 l2 m n – 14 l m2 n – 13 l2 n2 + 12 l m n2 + m2 n2) + 2 a2 b2 l m n2 (n – l) (m – n) (l – m)2 (13 l2 m2 – 12 l2 m n – 12 l m2 n – l2 n2 + 14 l m n2 – m2 n2))
/ (256 Δ (l – m)2 (l – n)2 (m – n)2 (l m – l n – m n) (l m + l n – m n) (l m – l n + m n))
–
DT-Coordinates QG-P11 in 3 QA-Quadrigons (only coordinates of 1st Quadrigon point are given)
( (3 S2 p2-Sa Sb p2-Sb2 q2-Sc a2 r2)(-p2+q2+r2)+Sb q2 (( Sa+c2) p2+Sb q2-(a2+ Sc) r2) :
(-p2+q2+r2) ((S2-Sa2) p2-4 S2 q2-(S2-Sc2) r2)+2 q2 (5 S2 r2+Sa c2 p2+Sb Sc r2) :
(3 S2 r2-Sc Sb r2-Sb2 q2-Sa c2 p2)(-r2+q2+p2)+Sb q2 (( Sc+a2) r2+Sb q2-(c2+ Sa) p2))
DT-Coordinates QG-P11 in 3 QL-Quadrigons (only coordinates of 1st Quadrigon point are given)
(m2 (-Sb a2 l2+(S2+ Sb Sc) m2-(S2-Sb2) n2) :
(l2-m2) (Sb Sc m2+S2 n2)-(3 S2 l2-2 S2 m2+Sa Sb m2) (m2-n2) :
-m2 ((S2-Sb2) l2-(Sa Sb+S2) m2+Sb c2 n2))
DT-Area of QG-P11-Triangle in the QA-environment
S/32 + 3(Sa p2+Sb q2+Sc r2)2 / (32 S (-p+q+r) (p+q-r) (p-q+r) (p+q+r))
DT-Area of QG-P11-Triangle in the QL-environment
3 S/32 – (Sc (l2-m2)2 n2+Sb m2 (l2-n2)2+Sa l2 (m2-n2)2)2 / (32 S (l2-m2)2 (l2-n2)2 (m2-n2)2)
Properties
- QG-P8, QG-P9, QG-P10, QG-P11 are collinear on QG-L5, the 2nd QG-Quasi Euler Line.
- QG-P11 is the Nine-point center of the 2nd QG-Quasi Diagonal Triangle: QG-Tr2.
- QG-P11 is the Midpoint of QG-P1 and QG-P7.
- The Midpoint of QA-P1 and QA-P2 lies on the circumcircle of the triangle formed by the three 2nd Quasi Nine-point Centers in a Quadrangle.
- Let Ni be the Nine-point centers of the Component Triangles Pj.Pk.Pl of the Reference Quadrigon. Now QG-P11 is the Diagonal Crosspoint of the Quadrigon formed by the Midpoints(Pi, Ni) (Eckart Schmidt, September 18, 2012).
Estimated human page views: 628
