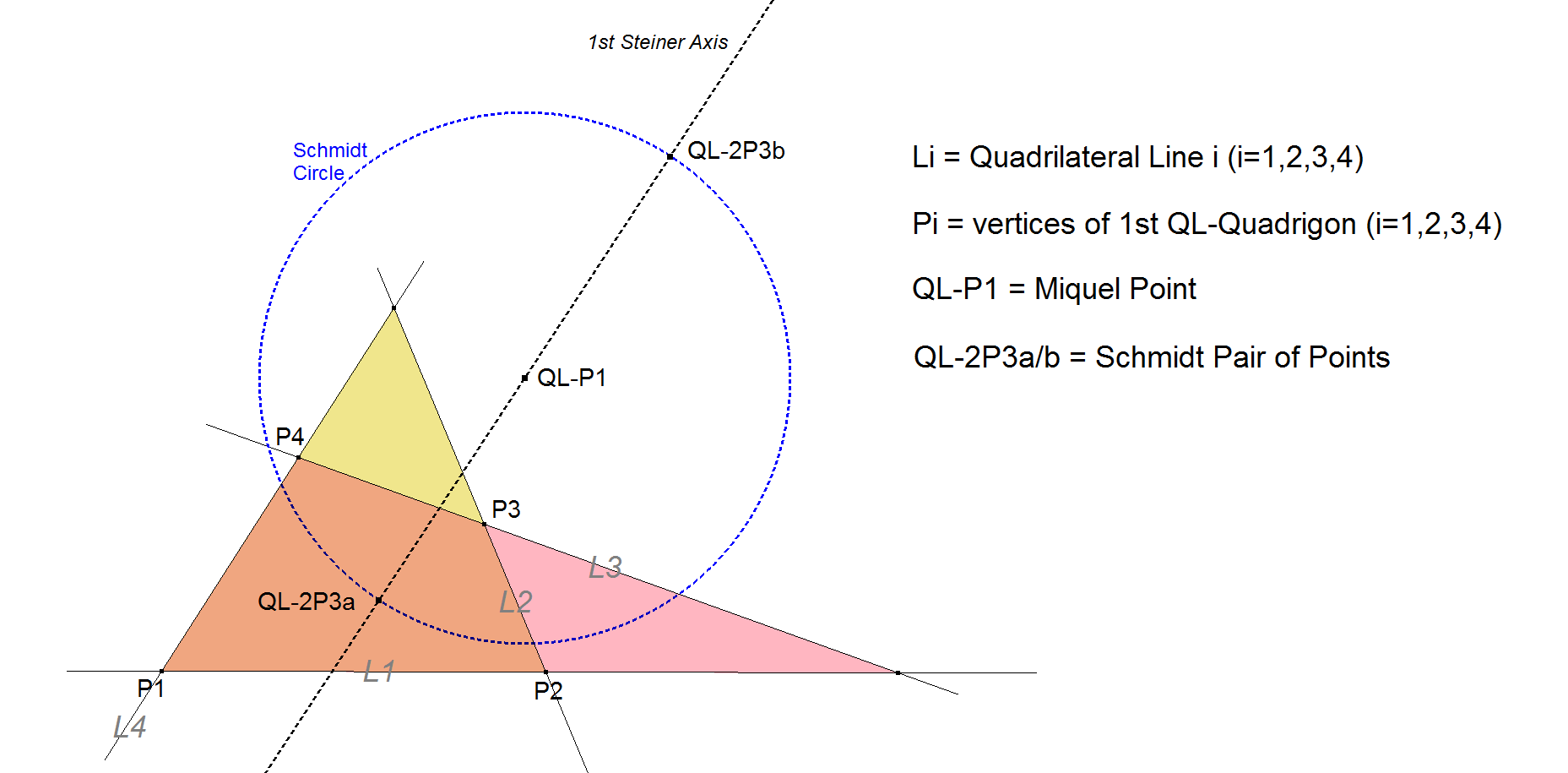
QL-2P3: Schmidt Pair of Points
Let the circle with Center QL-P1 and with radius = √[MA.MC] = √[MB.MD] be called the Schmidt Circle.
The Clawson-Schmidt Conjugate of a point P is the Inversion wrt the Schmidt Circle of the Reflection in the 1st Steiner Axis. See QL-Tf1.
The Schmidt Pair of Points QL-2P3a and QL-2P3b are those 2 points that are invariant wrt the Clawson-Schmidt Conjugate QL-Tf1. They are the intersection points of the Schmidt Circle and the 1st Steiner Axis (see QL-Tf1).
Coordinates:
When the Miquel triangle is reference triangle ABC (with C in the Miquel point), then the barycentric coordinates of QL-2P3a/b are:
- ( a(a+b+√((a+b)2-c2) : b(a+b+√((a+b)2-c2) : -c2),
- ( a(a+b -√((a+b)2-c2) : b(a+b -√((a+b)2-c2) : -c2).
See [34], QFG # 337 by Eckart Schmidt.
Properties
- For each QL-Quadrigon Pi, Pi+2, QL-2P3a/b and Pi+1, Pi+3, QL-2P3a/b are concyclic. See [34], QFG # 348 by Eckart Schmidt.
- For each QL-Quadrigon circumcircles through Pi, Pi+1, QL-2P3a/b and Pi+2, Pi+3, QL-2P3a/b are tangent in QL-2P3a/b. See [34], QFG # 348 by Eckart Schmidt.
- QL-2P3a and QL-2P3b are both the Isogonal Center (QA-P4) of their pedal quadrangle. See [34], QFG # 348 by Eckart Schmidt.
Estimated human page views: 672
