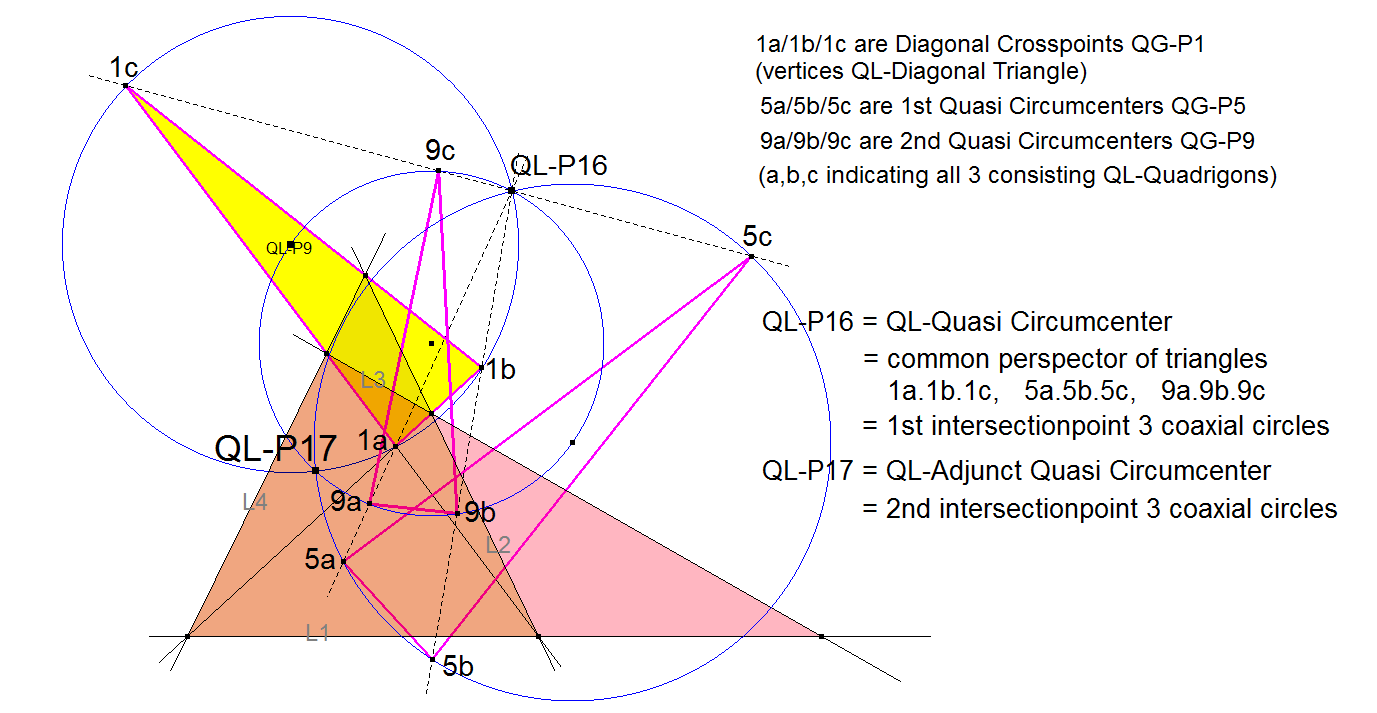
QL-P17: QL-Adjunct Quasi Circumcenter

QL-P17 is the 2^nd common intersection point of the coaxal circumcircles of the 3 triangles formed by the 3 QL-versions of resp. QG-P1, QG-P5, QG-P9.

The 1^st intersection point of these circles is QL-P16 (QL-Quasi Circumcenter).

1^st CT-coordinate

m n (a² (l – m) (l – n) (2 l² (m – n)² – m² n² + l m n (m + n))

+ b² (m – n) (m – l) n l (-3 l m + l n + m n)

+ c² (n – m) (n – l) m l (l m – 3 l n + m n)))

1^st DT-coordinate

a² m² n² / (m²-n²)

Properties

• QL-P17 lies on these lines:
  • QL-P8.QL-P25            (-2 : 3)
  • QL-P13.QL-P24
  • QA-P3.QG-P13
• QL-P17 is the AntiComplement of QL-P25 wrt the QL-Diagonal Triangle.
• QL-P17 is the Reflection of QL-P24 in the line QL-P6.QL-P9.
• QL-P25 lies on the polar of QL-P17 wrt the Polar Circle of the QL-Diagonal Triangle (note Eckart Schmidt).
• QL-P17 lies on the circumcircles of triangles formed by the 3 QL-versions of QG-P1 (being QL-Diagonal Triangle QL-Ci1), QG-P5 as well as QG-P9.
• QL-P17 lies on the Dimidium Circle QL-Ci6. The second intersection point with the circumcircle of the QL-Diagonal Triangle (QL-Ci1) is QL-P24.
• QL-P17 is the Miquel Point (QL-P1) of the Quadrilateral formed by the lines of the QL-Diagonal Triangle and the Newton Line (QL-L1). See [34], message # 164 and accompanying document “Diagonal Quadrilaterals and Conics through the points S1,S2,S3” page 2 of Bernard Keizer.

Estimated human page views: 495