← Previous Next →

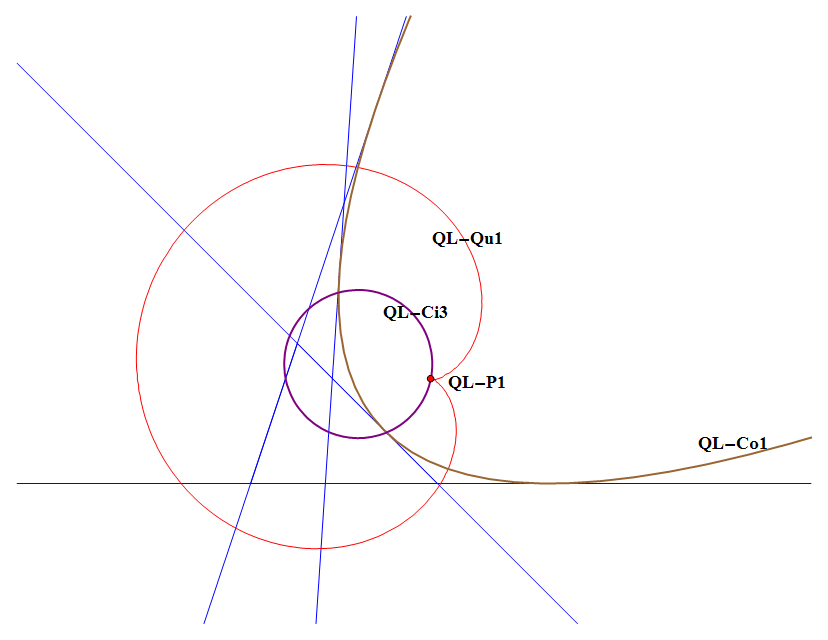
QL-Qu1: Morley’s Mono Cardioid

QL-Qu1 is the Cardioid which is the envelope of the circles through fixed point QL-P1 (Miquel Point) and with circumcenter on QL-Ci3 (Miquel Circle).

The equation is of the 4th degree, so it is a quartic.

QL-Qu1 was described by F. Morley in his document “Extensions of Clifford’s Chain-Theorem”. See [37]. There he describes that in a Quadrilateral (4-Line) one single Cardioid will occur enveloping the 4 circumcircles of the Component. Also he describes that there will be 27 possible Cardioids (QL-27Qu1) that can be inscribed in a Quadrilateral (4-Line). He describes also the numbers of other epicycloids occurring in a n-Line.

QL-Qu1 is described by Eckart Schmidt (see [15d]) and by Bernard Keizer in his document at [43] as well as in [34], QFG #514, #918.

Infovisual QL-Qu1-infovisual-cvt-01.gif
Construction methods:

QL-Qu1 is the locus of the reflections of QL-P1 in tangents at QL-Ci3 (QFG#918).

QL-Qu1 is the QL-Tf1 image of the inscribed parabola QL-Co1 (QFG#918).

Consider a circle through QL-P1 and centered in the reflection of QL-P1 in QL-P4. The pedal points of QL-P1 wrt tangents at this circle give the cardioid (QFG#918).

QL-Cu1 is the Catacaustic (see [13]) of a circle round QL-P4 through the ratiopoint QL-P1.QL-P4 (4:-3). Rays from this point envelop with their reflections at the circle the cardioid (QFG#918).

Another way of constructing the mono-Cardioid is passingly described by F. Morley at [47] page 20. Take 2 circumscribed circles of Component Triangles in the Quadrilateral. They are tangent to the Cardioid in 2 points: the Miquel point QL-P1 and one vertice of the Quadrilateral. Take a variable line through this vertice, it cuts the 2 circles in 2 points and the tangents to the 2 circles in these points intersect on the Cardioid (see also [34], QFG-message #811 of Bernard Keizer).

Equation in CT-notation

a4 (m – n)2 Ta2 + b4 (l – n)2 Tb2 + c4 (l – m)2 Tc2

+ 2 a2 b2 (n – l) (n – m) Ta Tb + 2 b2 c2 (l – m) (l – n) Tb Tc + 2 a2 c2 (m – l) (m – n) Tc Ta = 0

where:

Ta = a2 ( l – m) ( l – n) y z + c2 ( l – n) y (l x + m y + m z) + b2 (l – m) z ( l x + n y + n z)

Tb = b2 (m – l) (m – n) x z + c2 (m – n) x (l x + m y + l z) + a2 (m – l) z (n x + m y + n z)

Tc = c2 (n – m) (n – l) x y + b2 (n – m) x (l x + l y + n z) + a2 ( n – l) y (m x + m y + n z)

Equation in DT-notation

(l2 – n2) (m2 – n2) (-2 a2 b2 n (m x + l y) z + a4 m n z (x – y + z) + b4 l n z (-x + y + z) –

c4 l m z (x + y + z) – 2 b2 c2 l (-l2 x2 + (y + z) (m2 y + l2 z)) + 2 a2 c2 m (-m2 y2 + (x + z) (l2 x + m2 z)))2

+ (l2 – m2) (l2 – n2) (b4 l n x (x + y – z) + c4 l m x (x – y + z) – a4 m n x (x + y + z) – 2 b2 c2 l x (n y + m z) + 2 a2 b2 n ((x + y) (n2 x + m2 y) – n2 z2) – 2 a2 c2 m (-m2 y2 + (x + z) (m2 x + n2 z)))2

– (l2 – m2) (m2 – n2) (a4 m n y (x + y – z) + c4 l m y (-x + y + z) – b4 l n y (x + y + z)

– 2 a2 c2 m y (n x + l z) – 2 a2 b2 n ((x + y) (l2 x + n2 y) – n2 z2) + 2 b2 c2 l (-l2 x2 + (y + z) (l2 y + n2 z)))2 = 0

Properties
  • The cusp of the Cardioid is at QL-P1, the Miquel Point.
  • The inner circle of the Cardioid is QL-Ci3 (Miquel Circle).
  • QL-Qu1 is the Clawson-Schmidt conjugate of the inscribed QL-Parabola QL-Co1.
  • The angle between the axis of the Cardioid and the axis of the inscribed QL-Parabola QL-Co1 is ∑θi, where θi represents the angles between the Steiner Line and the lines Li (i=1,2,3,4) of the Reference Quadrilateral (Bernard Keizer, April 17, 2013).
  • QL-Qu1 is tangent to the 4 circles circumscribing the 4 Component Triangles of the Reference Quadrilateral (Bernard Keizer, April 17, 2013).


Estimated human page views: 620

Scroll naar boven